5. Toisen asteen polynomifunktio
Toisen asteen polynomifunktio on muotoa f(x)=ax2+bx+c missä a, b ja c ovat vakioita ja a ≠ 0.
Toisen asteen polynomifunktion kuvaaja on paraabeli.
Esimerkki 1.
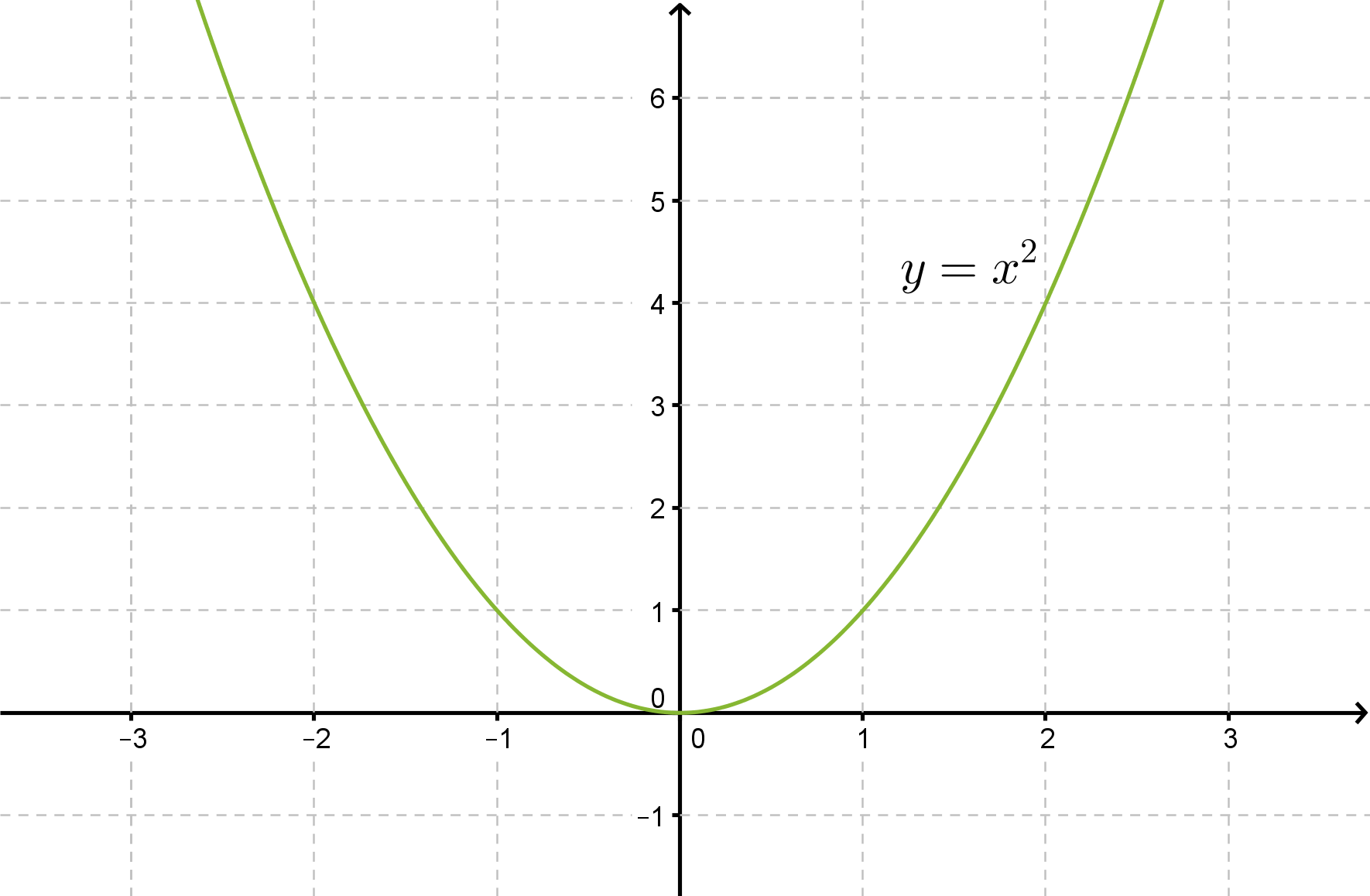
Yksinkertaisin toisen asteen polynomifunktio on muotoa f(x) = x2. Lasketaan muutamia käyrän y = x2 pisteitä, sijoitetaan ne koordinaatistoon ja yhdistetään kuvaajaksi. Tätä paraabelia kutsutaan perusparaabeliksi.
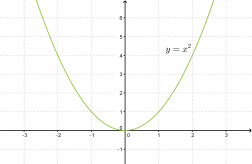
Klikkaa kuva suuremmaksi!
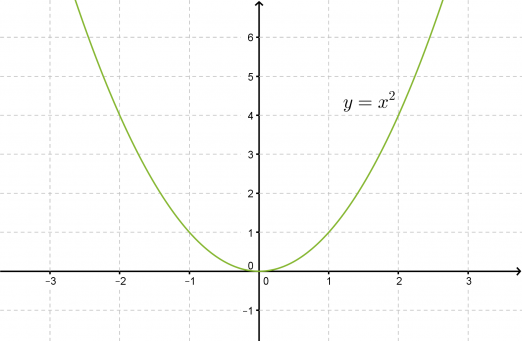
Klikkaa kuva suuremmaksi!
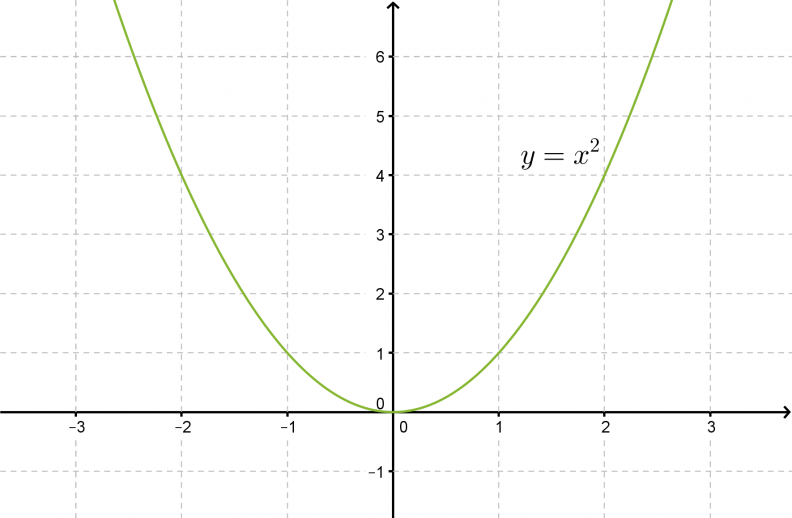
Klikkaa kuva suuremmaksi!
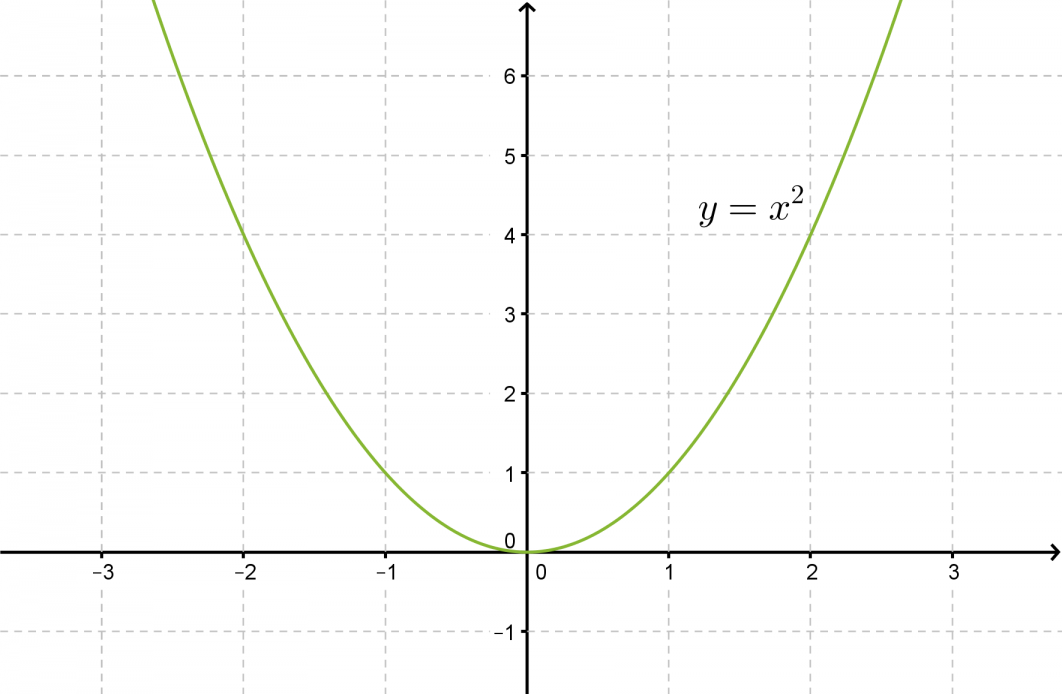
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Pisteitä ei saa yhdistää toisiinsa janoilla eli suorilla viivoilla. Tällöinhän olisi kyseessä monesta eri ensimmäisen asteen yhtälöstä muodostuva paloittain määritelty funktio. Ensimmäisen asteen funktion kuvaaja on suora, mutta korkeamman asteen funktioiden kuvaajat ovat aina käyräviivaisia.
Käyrä y = x2 on symmetrinen y-akselin suhteen. Paraabelin ja sen symmetria-akselin leikkauspistettä kutsutaan huipuksi. Kohtia, jossa kuvaaja leikkaa x-akselin, sanotaan paraabelin nollakohdiksi.
Esimerkki 2.
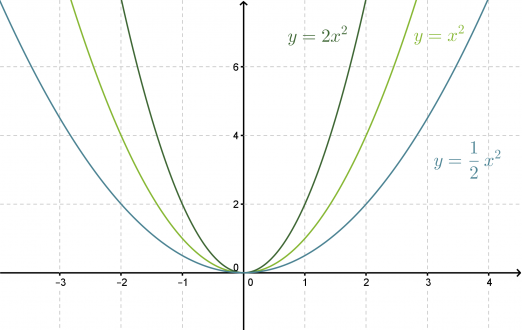
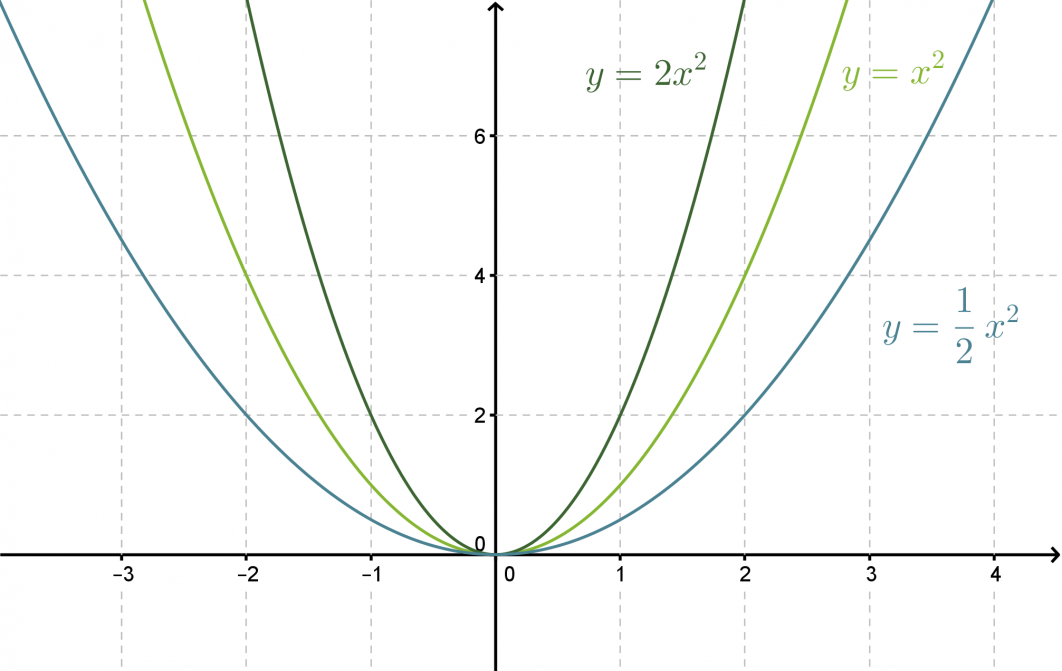
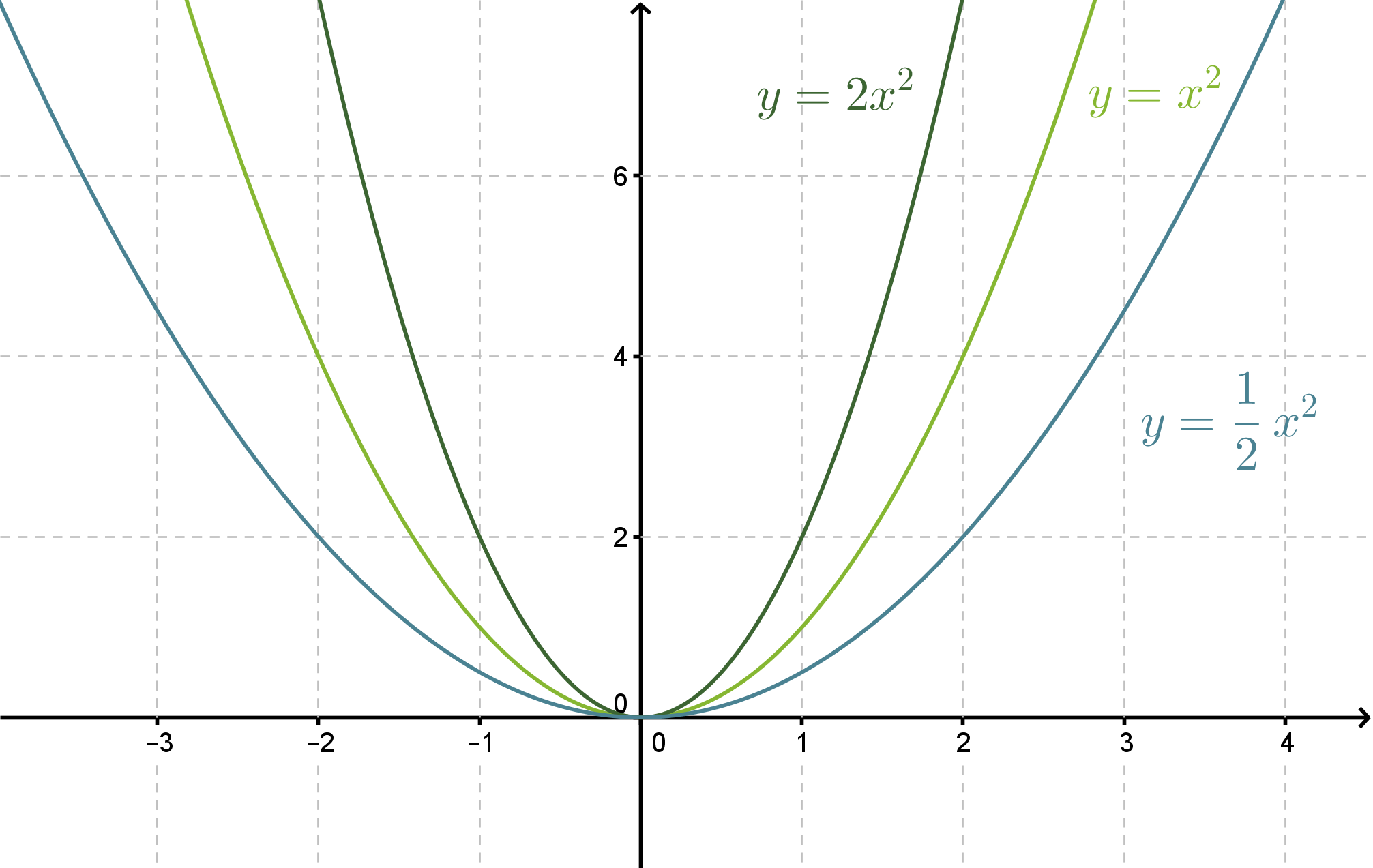
Tutkitaan muotoa f(x) = ax2 olevien funktioiden kuvaajia. Piirretään muutama käyrä koordinaatistoon vaihdellen kertoimen a arvoa.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
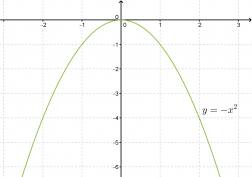
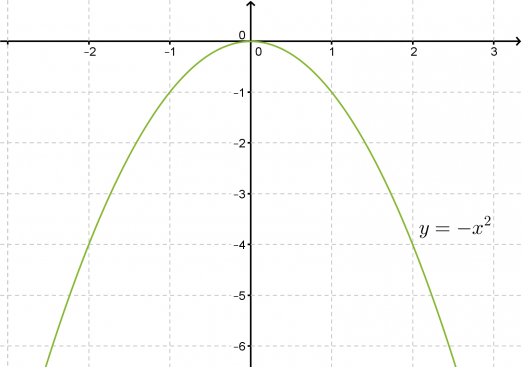
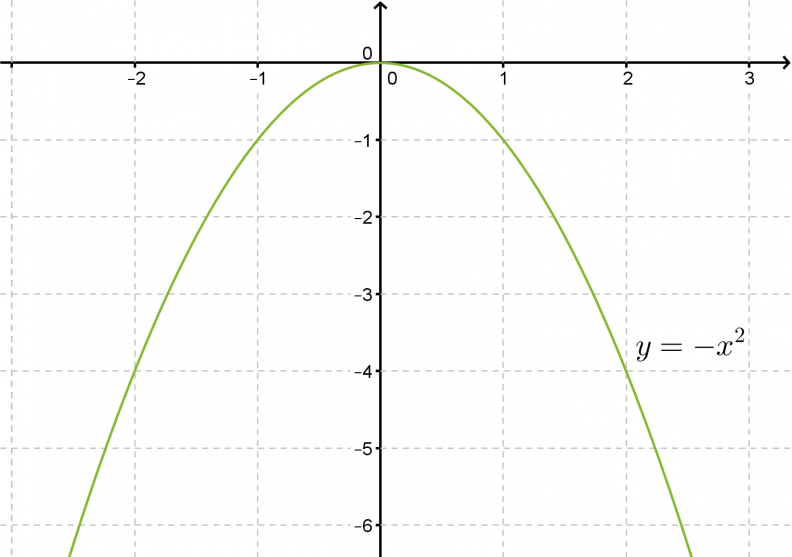
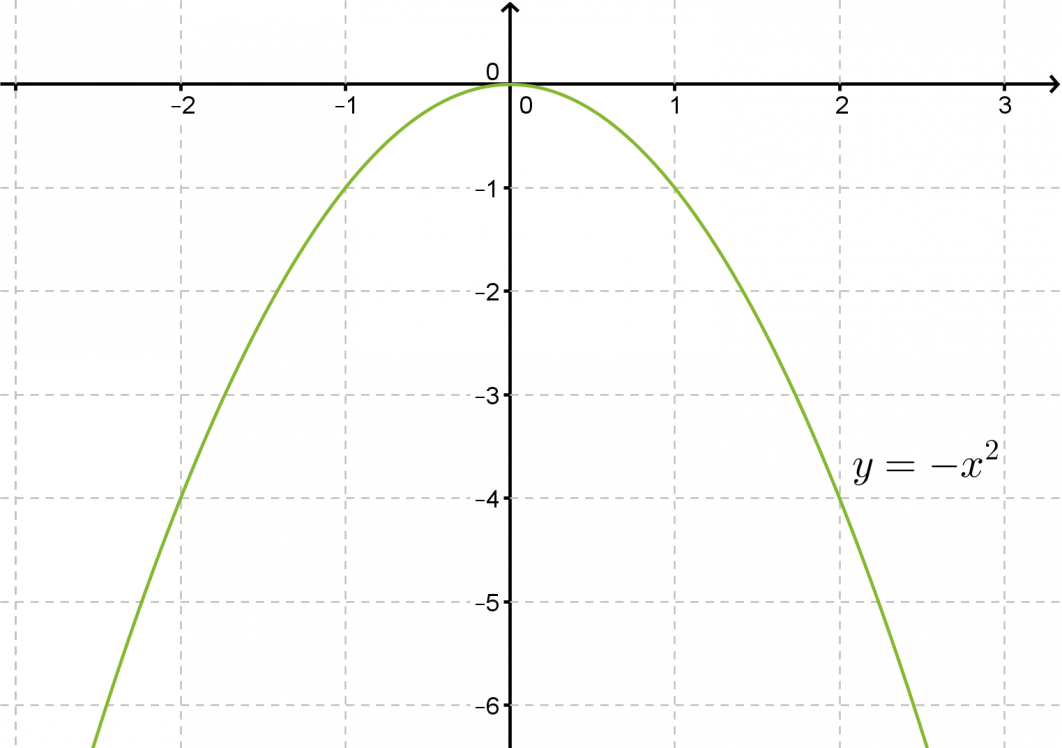
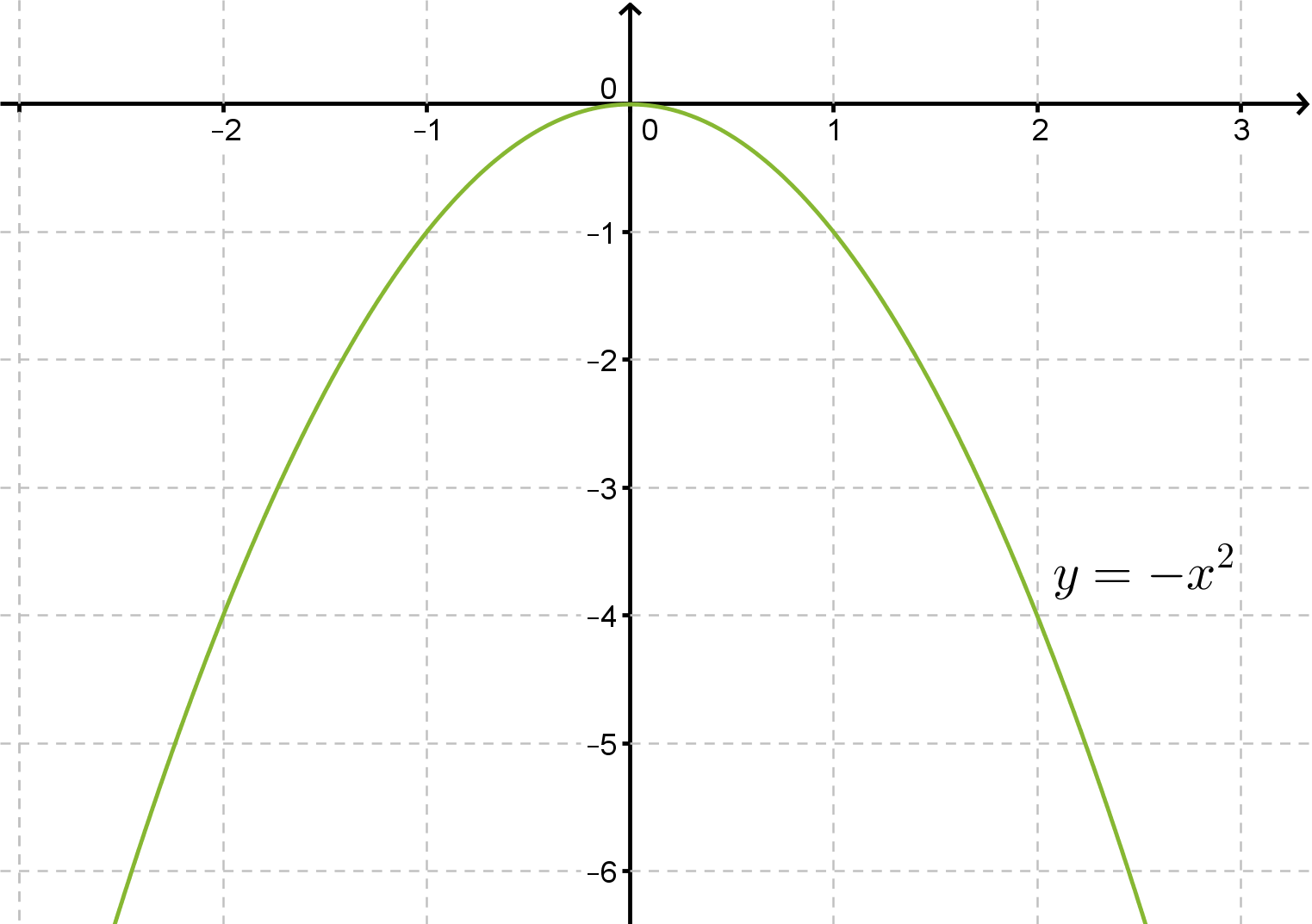
Toisen asteen muuttujan kerroin ei vaikuta symmetria-akselin tai käyrän huippupisteen sijaintiin, mutta sillä on selvä vaikutus paraabelin leveyteen. Paraabelin y = -x2 kuvaaja on puolestaan paraabelin y = x2 peilaus x-akselin suhteen.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jos polynomifunktion kuvaaja on ylöspäin aukeava paraabeli, funktio saa pienimmän arvonsa paraabelin huipussa, mutta funktion suurinta arvoa ei voida määrittää. Sen sijaan jos kuvaaja on alaspäin aukeava paraabeli, funktio saa suurimman arvonsa paraabelin huipussa, mutta funktion pienintä arvoa ei voida määrittää.
Esimerkki 3.
Esimerkin 2 funktioiden f(x) = 2x2, f(x) = x2 , f(x) = 1/2 x2pienin arvo on 0, mutta suurinta arvoa ei voida määrittää. Sen sijaan funktion f(x) = –x2 suurin arvo on 0, mutta pienintä arvoa ei voida määrittää.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014
Toisen asteen termin kertoimesta voidaan päätellä paraabelin aukeamissuunta ja muoto
paraabeli aukeaa ylöspäin.
paraabeli aukeaa alaspäin.
paraabeli on leveä.
paraabeli on kapea.