6. Vaillinaiset toisen asteen yhtälöt I

Toi­sen as­teen yh­tä­lön ylei­nen nor­maa­li­muo­to on

ax2 + bx + c = 0.

Jos yh­tä­lös­sä esiin­tyy kaik­ki ter­mit, sa­no­taan sitä täy­del­li­sek­si toi­sen as­teen yh­tä­lök­si. Jos ter­mi bx tai va­ki­o­ter­mi c puut­tuu, on ky­sees­sä vail­li­nai­nen toi­sen as­teen yh­tä­lö.

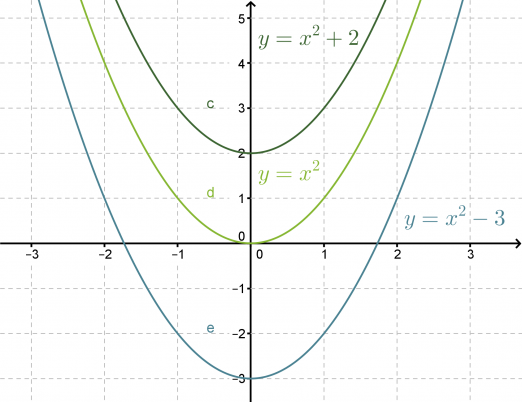
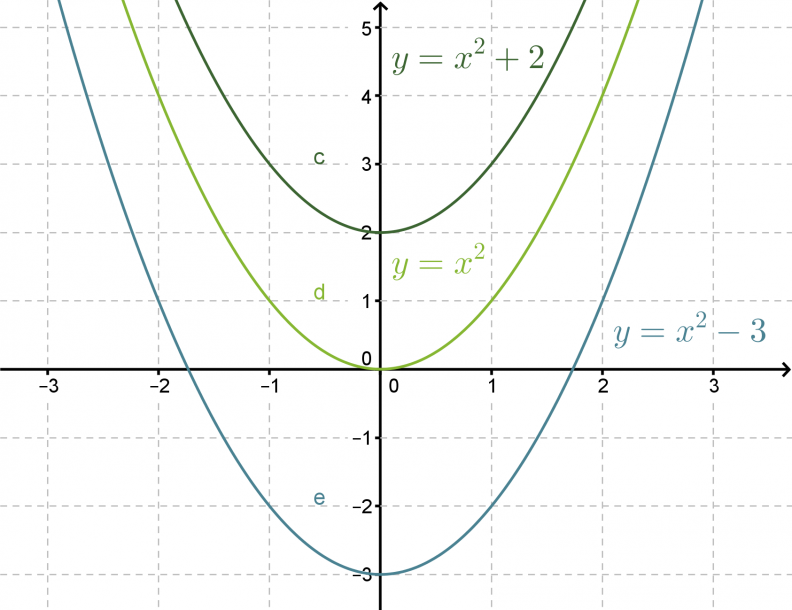
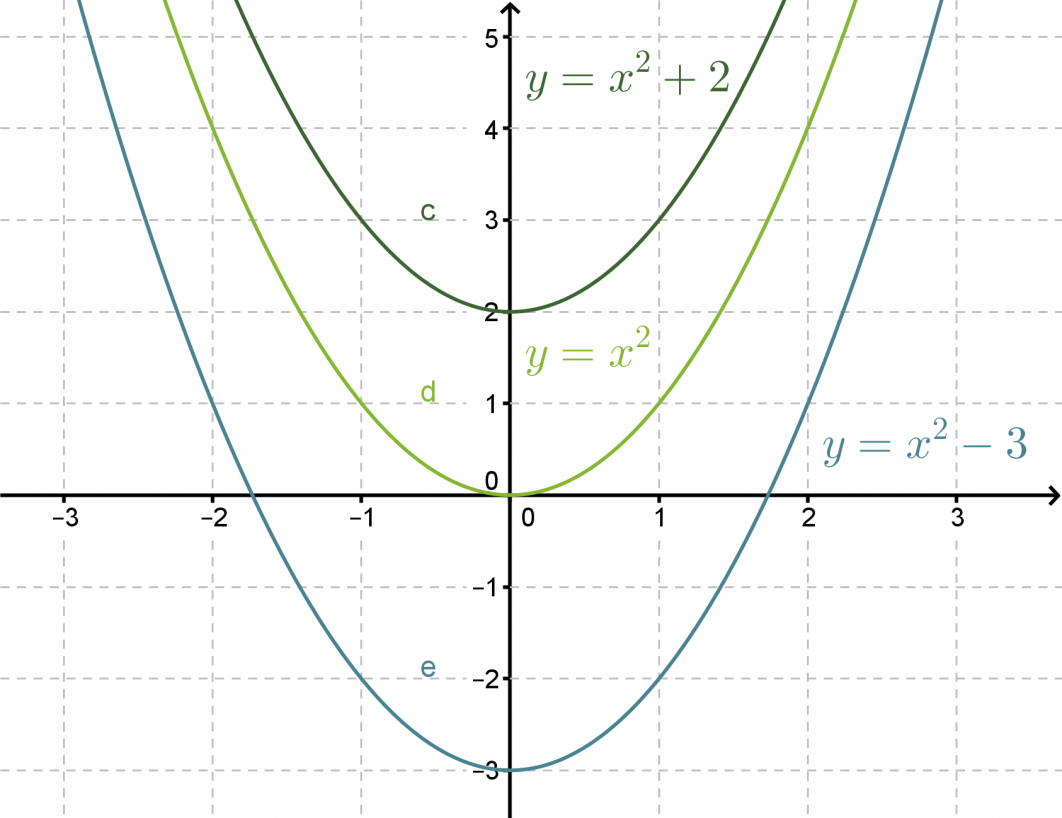
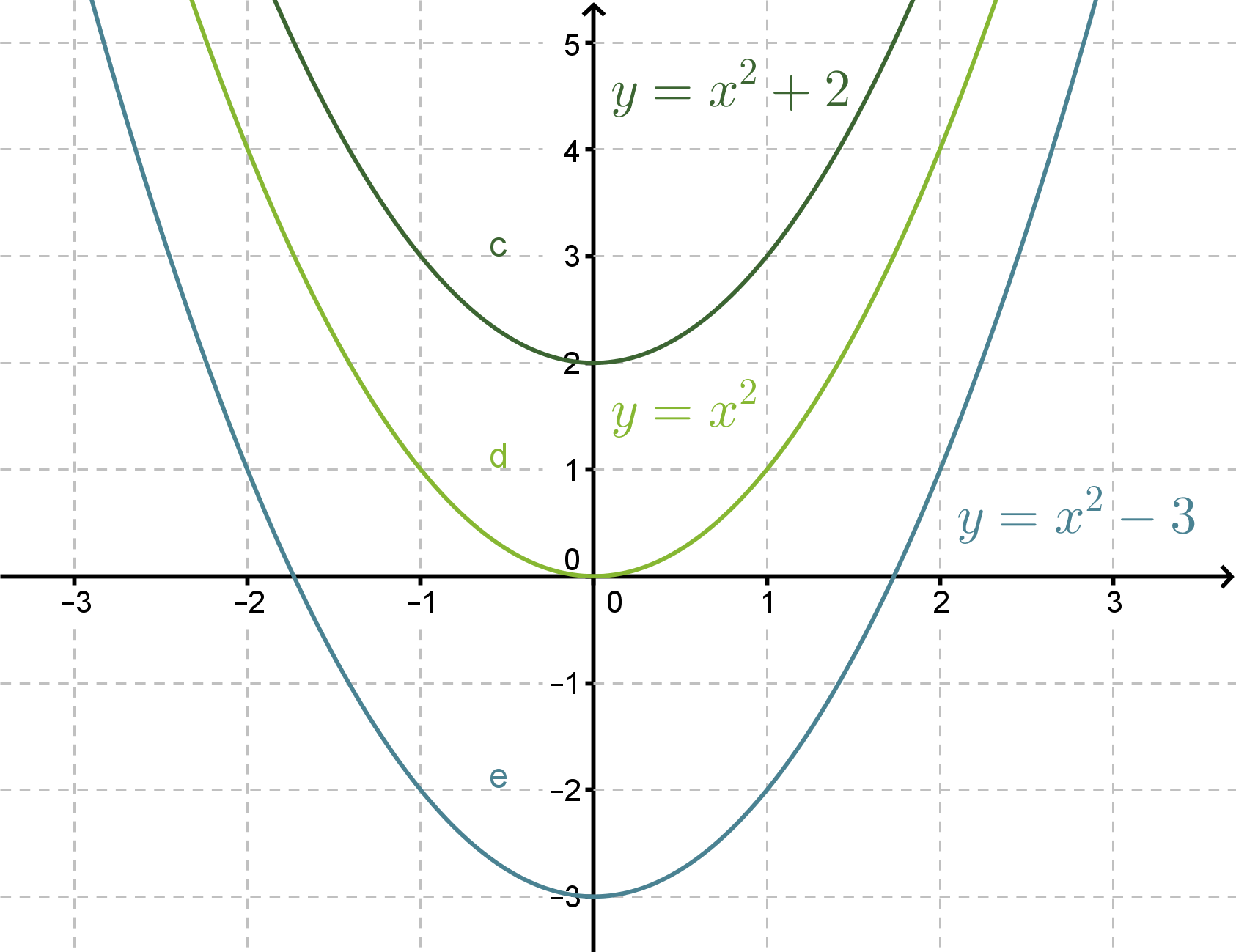
Vail­li­nai­sil­le toi­sen as­teen yh­tä­löil­le on ole­mas­sa rat­kai­su­ta­vat yh­tä­lön tyy­pis­tä riip­pu­en. Tut­ki­taan aluk­si muo­toa ax2 + c = 0 ole­via yh­tä­löi­tä. Piir­re­tään muu­ta­ma funk­ti­on f(x) = x2 + c ku­vaa­ja sa­maan koor­di­naa­tis­toon vaih­del­len va­ki­on c ar­voa.

Klik­kaa kuva suu­rem­mak­si!

Funk­ti­oi­den ku­vaa­jat ovat yh­te­ne­vät ja nii­den sym­met­ria-ak­se­li­na on y-ak­se­li. Va­kio c il­mai­see koh­dan, jos­sa pa­raa­be­lin huip­pu si­jait­see. Yh­tä­lön ax2 + c = 0 rat­kai­sut näh­dään ku­vaa­jas­ta nol­la­koh­ti­na, jois­sa ku­vaa­ja leik­kaa x-ak­se­lin. Nol­la­koh­tien mää­rä riip­puu sii­tä, onko funk­ti­os­sa esiin­ty­vä va­kio c po­si­tii­vi­nen vai ne­ga­tii­vi­nen.

Yhtälön ax2+c = 0 ratkaisujen määrä riippuu vakiosta c

Huom! Edel­li­nen pä­tee ai­no­as­taan ylös­päin au­ke­a­viin pa­raa­be­lei­hin. Mi­ten rat­kai­su­jen mää­rä riip­puu va­ki­os­ta c, jos a on ne­ga­tii­vi­nen?

Muotoa ax2+c = 0 olevan yhtälön ratkaiseminen

Huom! Ne­li­ö­juur­ta otet­ta­es­sa on huo­mi­oi­ta­va sekä po­si­tii­vi­nen että ne­ga­tii­vi­nen ta­paus, sil­lä ne­ga­tii­vi­nen kan­ta­luku toi­seen po­tens­siin ko­ro­tet­tu­na, on myös po­si­tii­vi­nen.

Esimerkki 1.

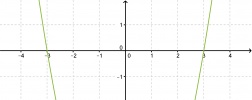
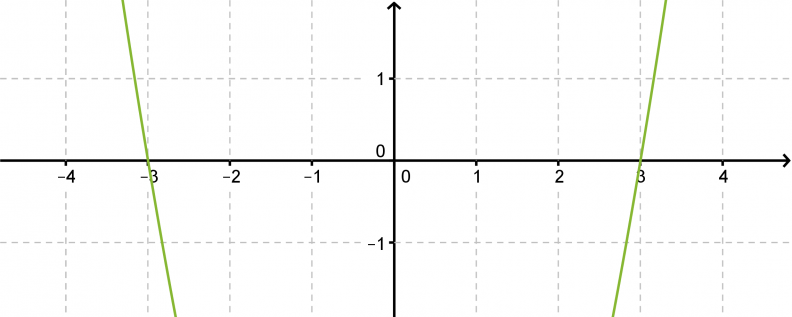
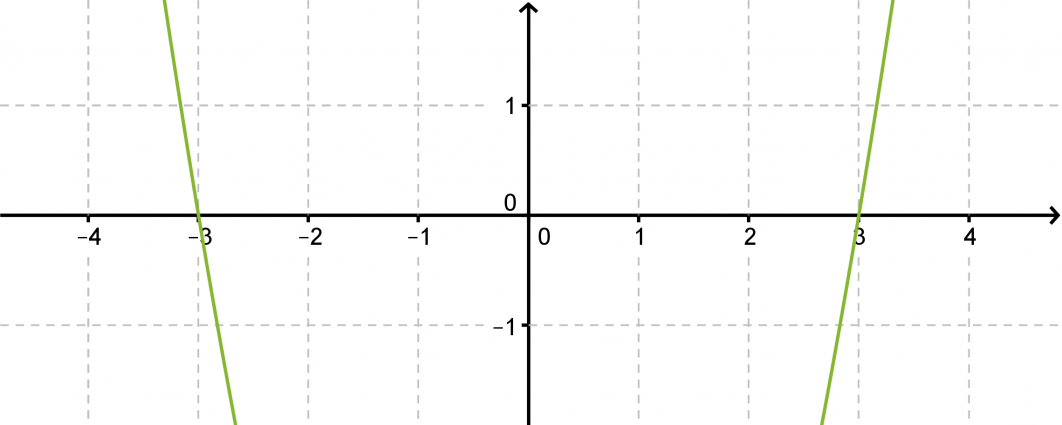
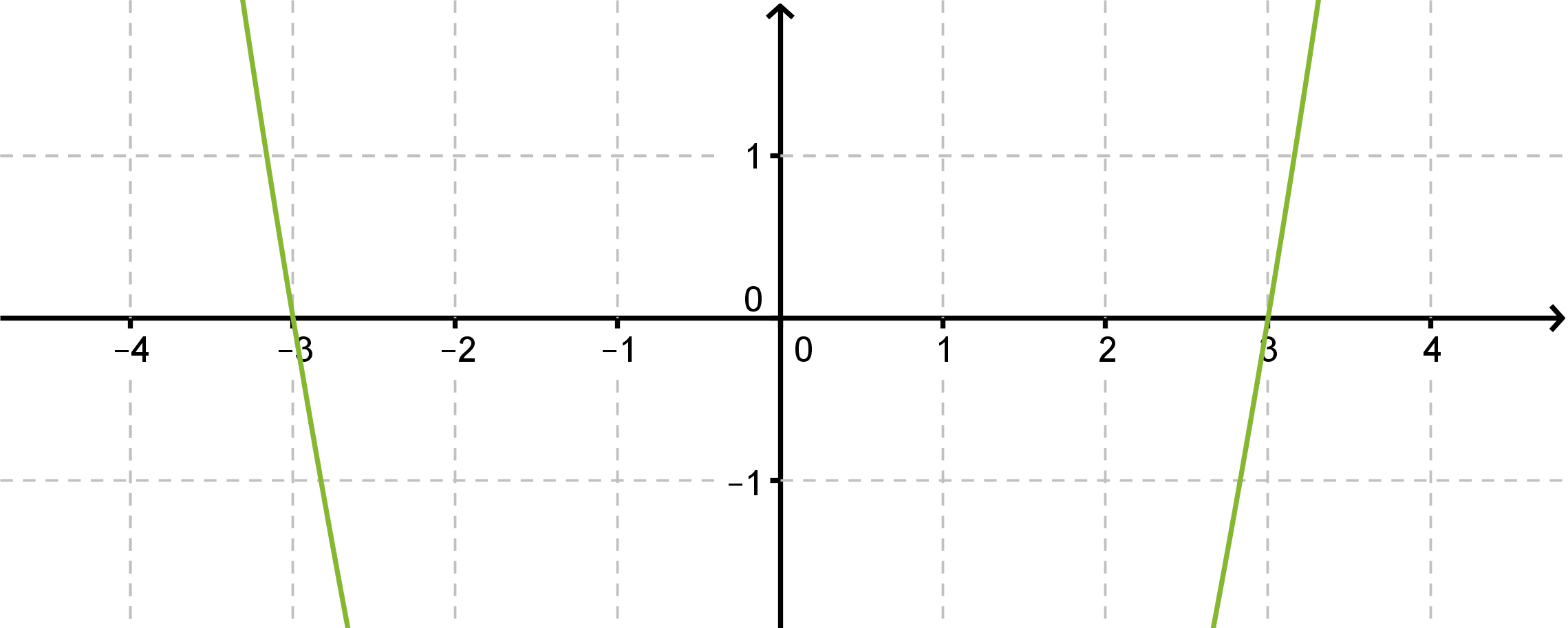
Rat­kais­taan yh­tä­lö ja hah­mo­tel­laan yh­tä­lön mää­rää­män pa­raa­be­lin ku­vaa­ja.

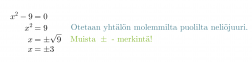
Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: x = 3 tai x = -3.

Esimerkki 2.

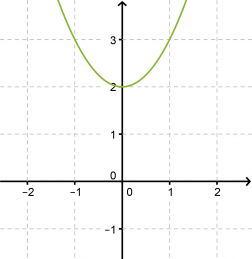
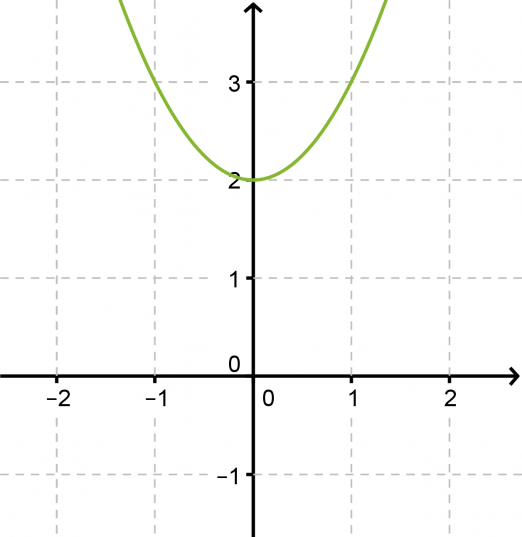
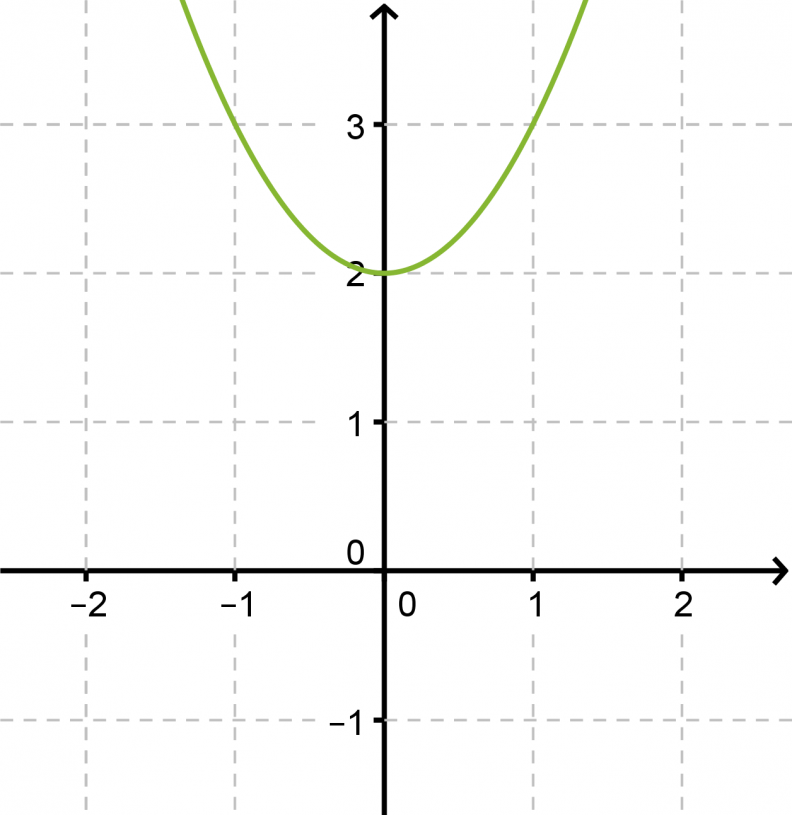
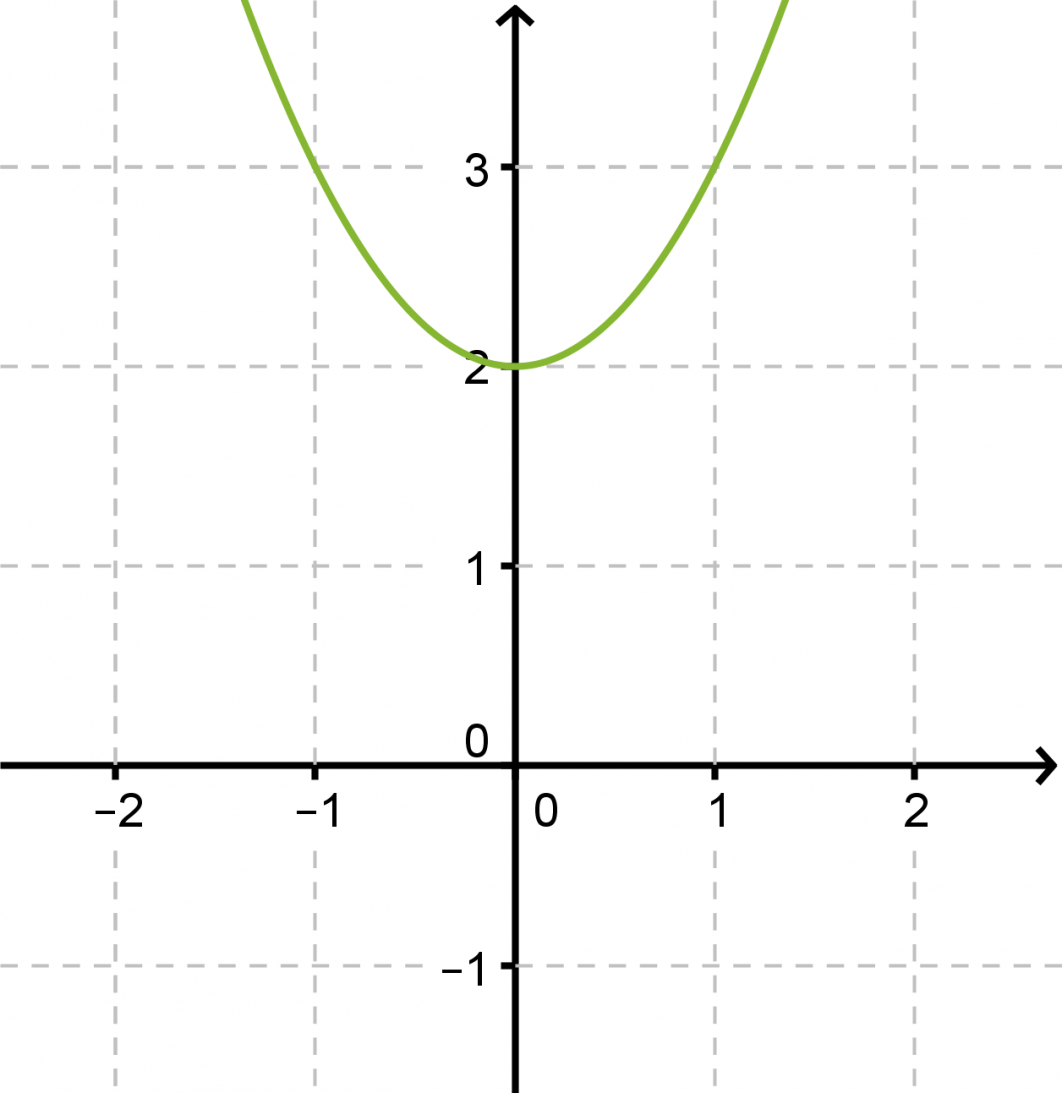
Rat­kais­taan yh­tä­lö 2x2 + 4 = 0 ja hah­mo­tel­laan yh­tä­lön mää­rää­män pa­raa­be­lin ku­vaa­ja.

Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Yh­tä­löl­lä ei ole rat­kai­sua.

Avoin ma­te­ma­tiik­ka 9Osio 3: Ker­ra­taan ja so­vel­le­taan5.6.2014