7. Vaillinaiset toisen asteen yhtälöt II

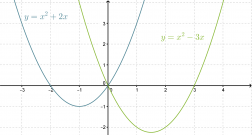
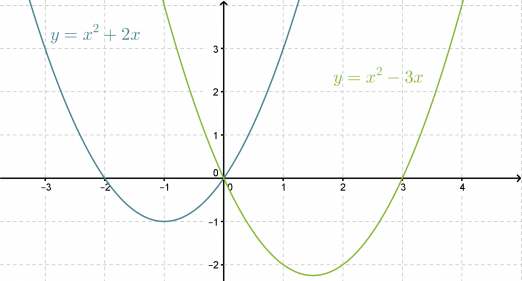
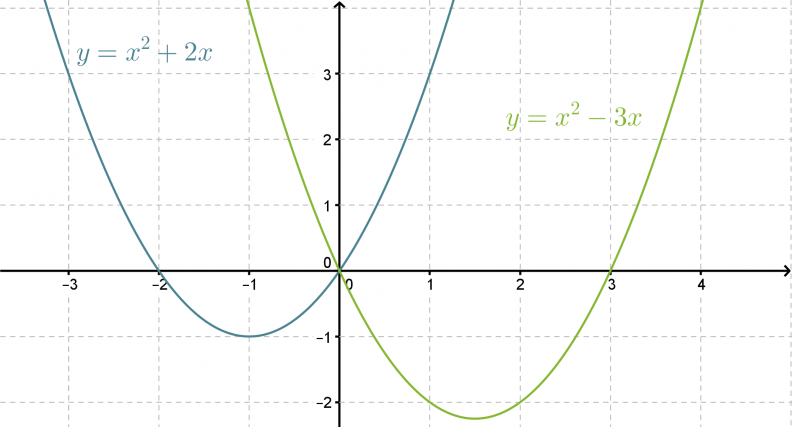
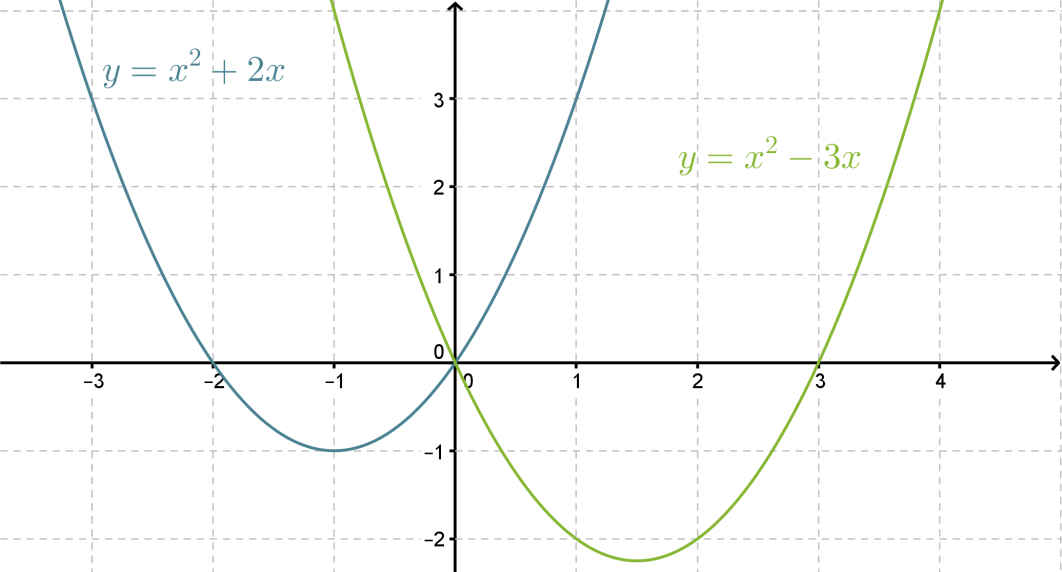
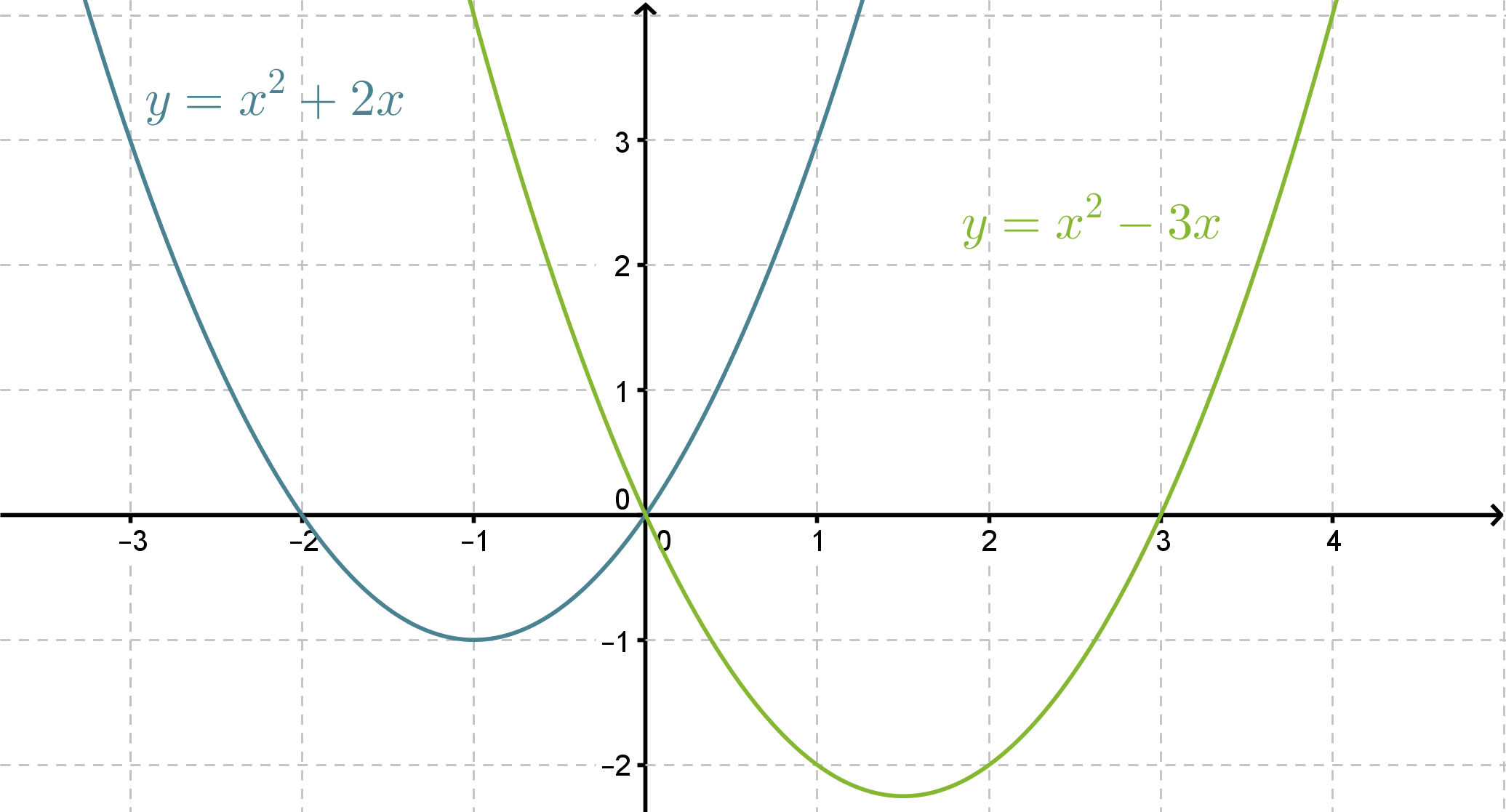
Piir­re­tään kak­si muo­toa f(x) = x² + bx ole­vaa vail­li­nais­ta toi­sen as­teen po­ly­no­mi­funk­ti­o­ta sa­maan koor­di­naa­tis­toon.

Klik­kaa kuva suu­rem­mak­si!

Funk­ti­oi­den ku­vaa­jat ovat yh­te­ne­vät. En­sim­mäi­sen as­teen ter­min ker­toi­mel­la b on sel­väs­ti yh­teys funk­ti­on toi­seen nol­la­koh­taan ja pa­raa­be­lin sym­met­ria-ak­se­lin si­jain­tiin.

Muo­toa y = ax² + bx ole­vat yh­tä­löt rat­ke­a­vat kä­te­vim­min te­ki­jöi­hin jaon kaut­ta.

Esimerkki 1.

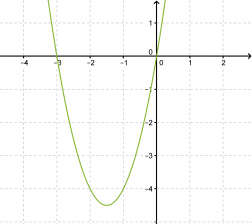
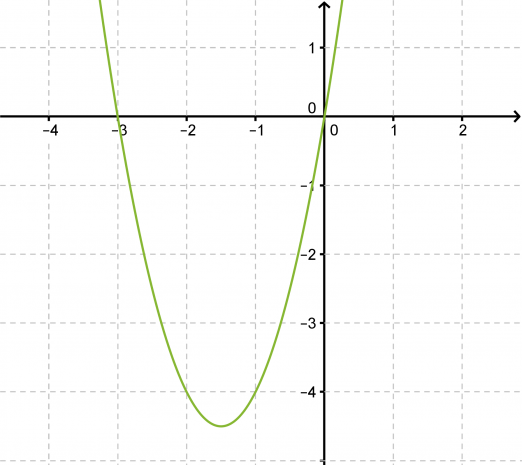
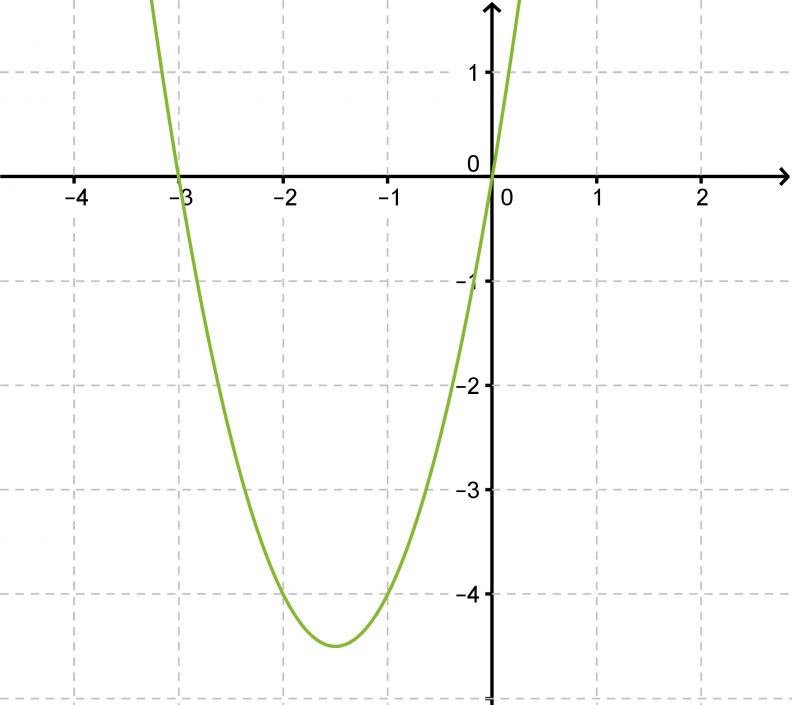
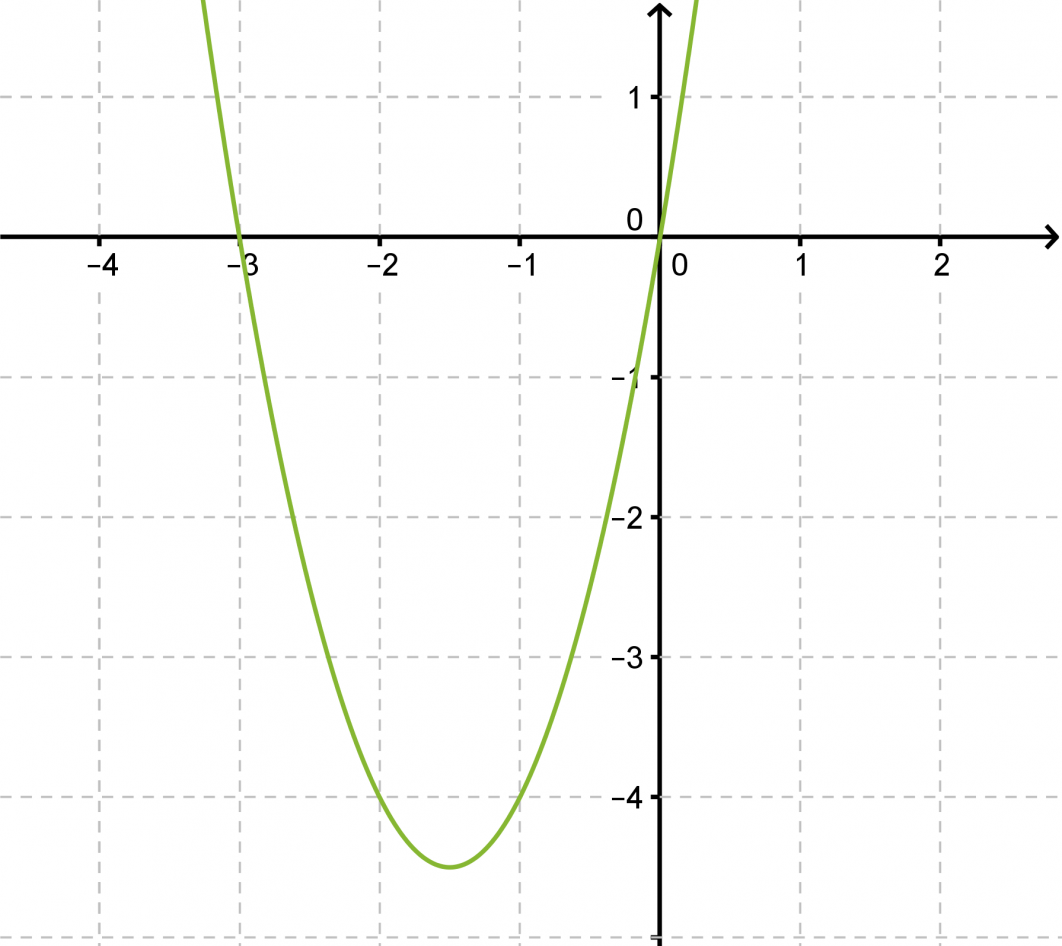
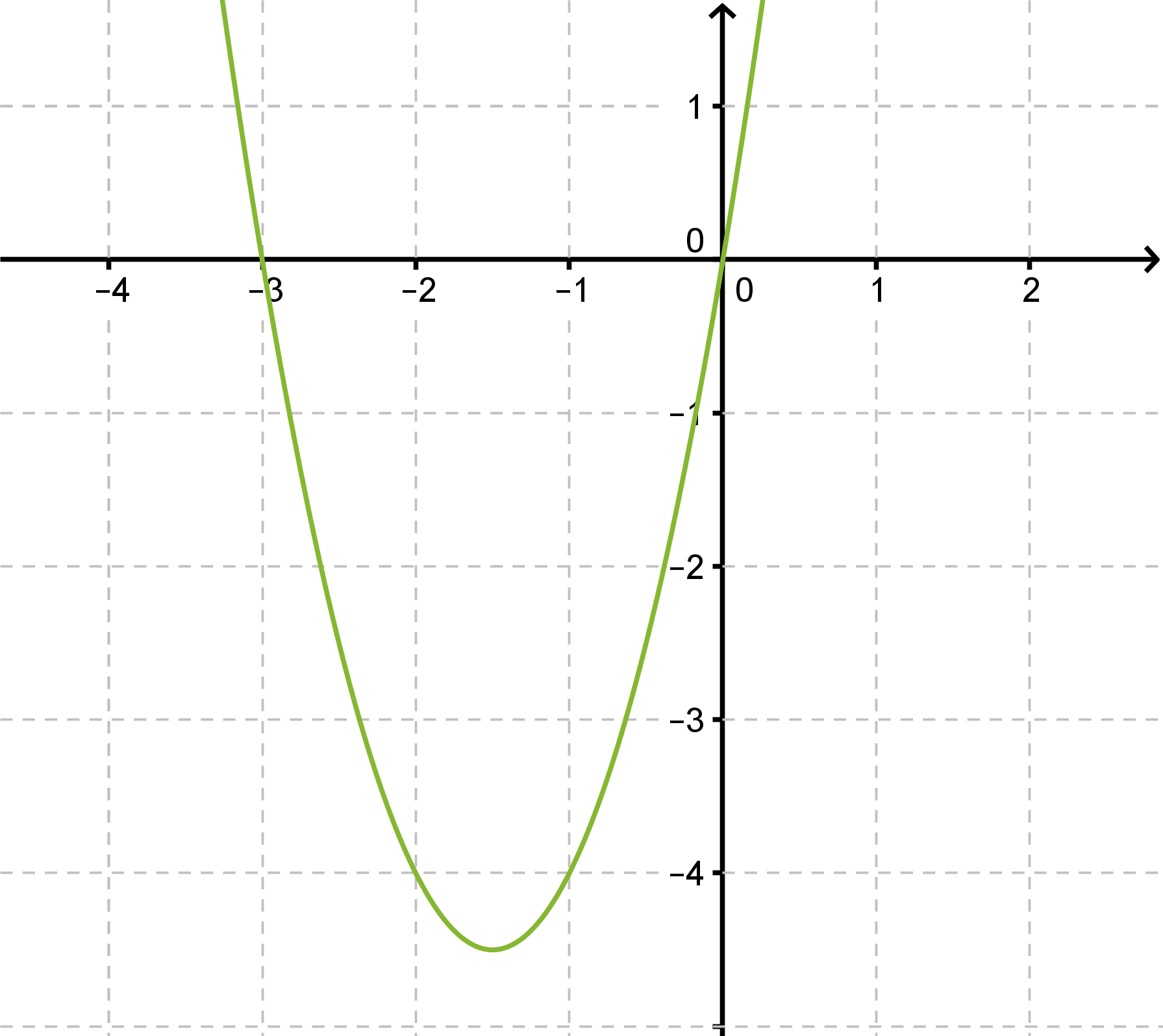
Rat­kais­taan yh­tä­lö 2x² + 6x = 0 ja hah­mo­tel­laan yh­tä­lön mää­rään pa­raa­be­lin ku­vaa­ja.

Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: x = 0 tai x = -3.

Esimerkki 2.

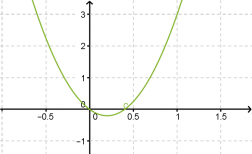
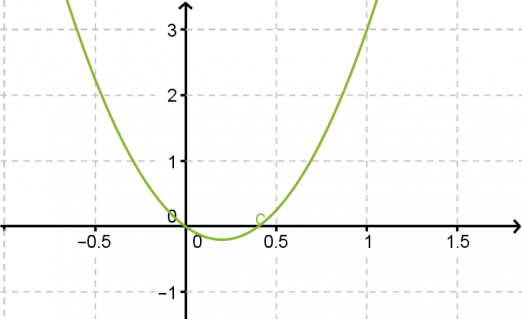
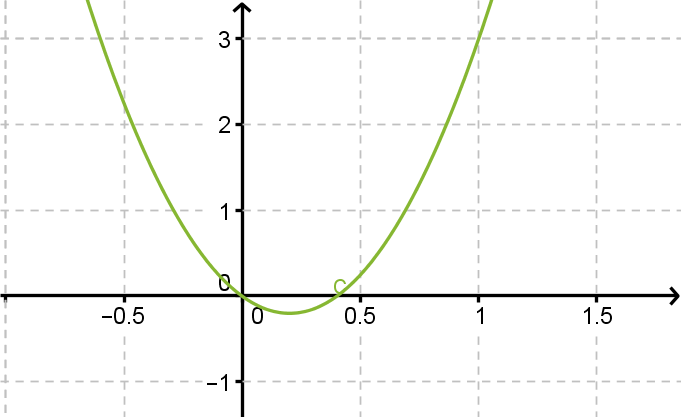
Rat­kais­taan yh­tä­lö 5x² – 2x = 0 ja hah­mo­tel­laan yh­tä­lön mää­rää­män pa­raa­be­lin ku­vaa­ja.

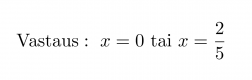
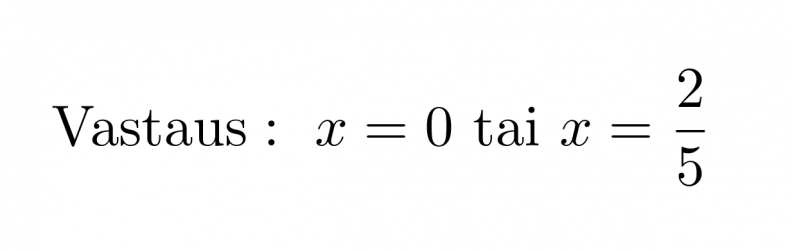
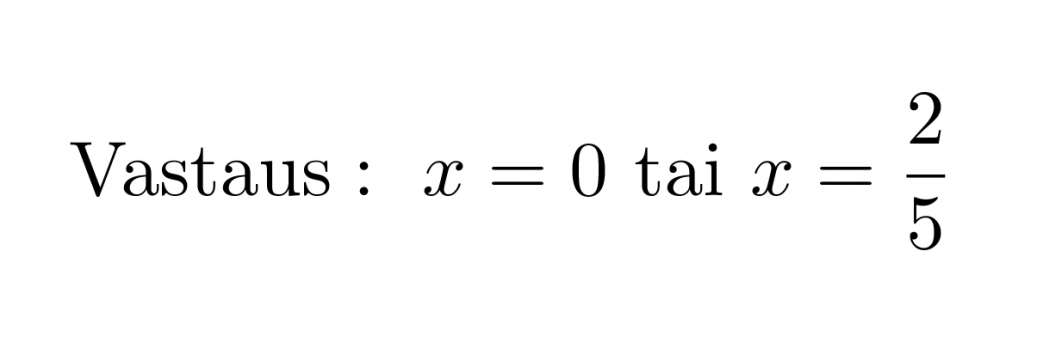
Klik­kaa kuva suu­rem­mak­si!

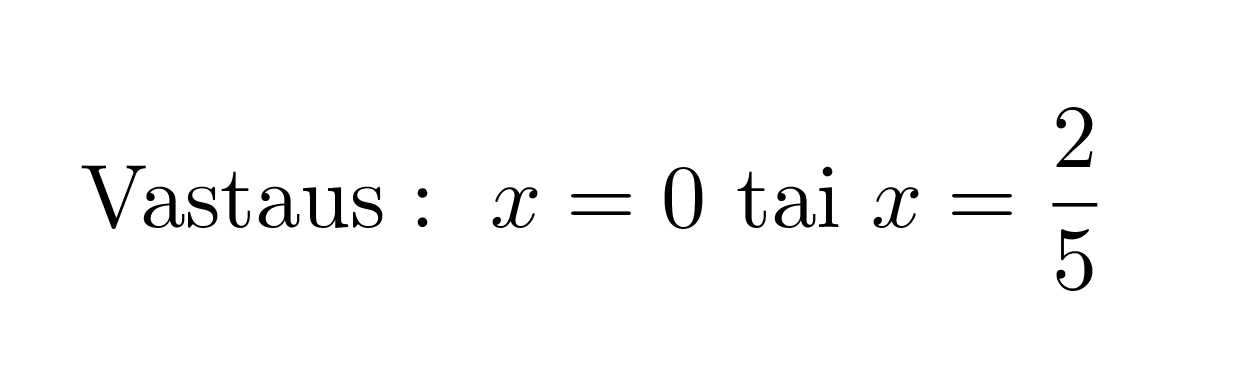
Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: x = 0 tai x = 2/5.