8. Murtolauseke*
Jos P ja Q ovat polynomeja (Q ≠ ()), niin lauseketta, joka on muotoa tai joka voidaan muuntaa muotoon

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
sanotaan murtolausekkeeksi.
Murtolauseke muodostuu siis jaettaessa polynomi toisella polynomilla. Murtolausekkeet käyttäytyvät samoin kuin murtoluvut ja niille on voimassa samat laskusäännöt. Osoittajassa ja nimittäjässä on vain yksittäisten lukuarvojen sijasta polynomit. Murtoluku on mahdoton, jos sen nimittäjässä on luku nolla, sillä nollalla ei voi jakaa. Samasta syystä murtolauseke on määritelty muualla, paitsi nimittäjän nollakohdissa.
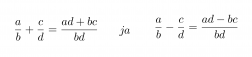
Klikkaa kuva suuremmaksi!
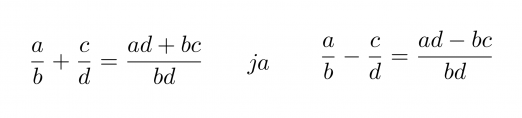
Klikkaa kuva suuremmaksi!
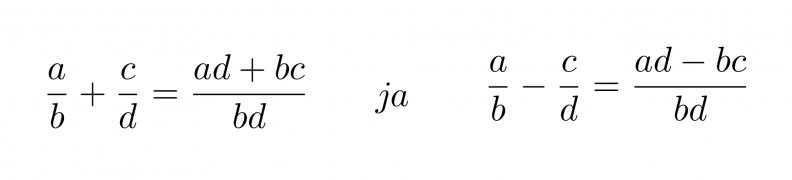
Klikkaa kuva suuremmaksi!
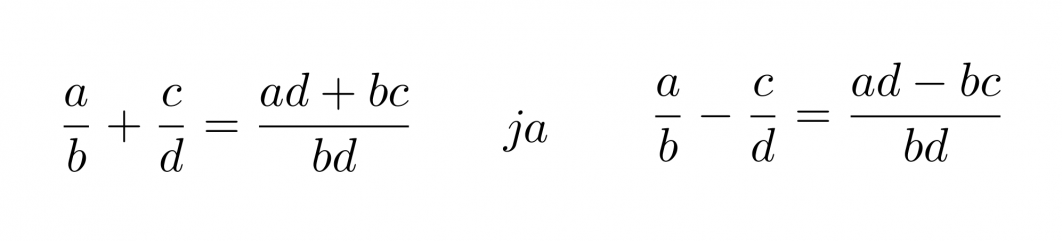
Klikkaa kuva suuremmaksi!
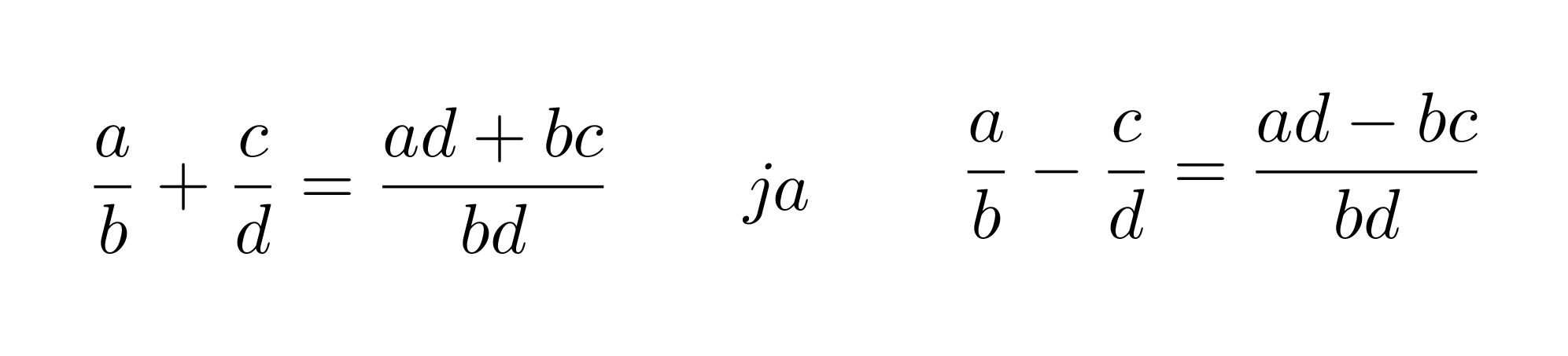
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
-
Murtolausekkeet kerrotaan keskenään siten, että osoittajat kerrotaan keskenään ja nimittäjät kerrotaan keskenään.
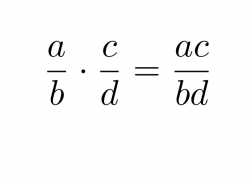
Klikkaa kuva suuremmaksi!
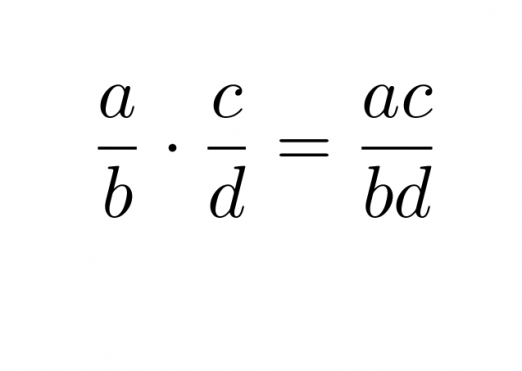
Klikkaa kuva suuremmaksi!
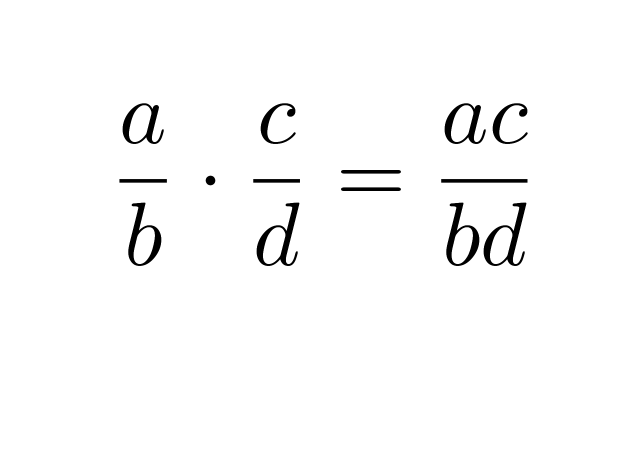
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
-
Murtolauseke jaetaan toisella murtolausekkeella siten, että se kerrotaan jakajan käänteisellä murtolausekkeella.
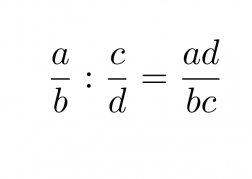
Klikkaa kuva suuremmaksi!
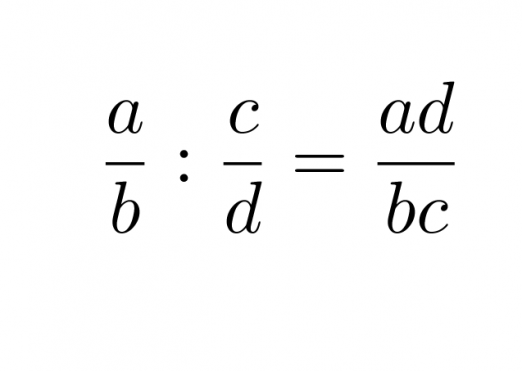
Klikkaa kuva suuremmaksi!
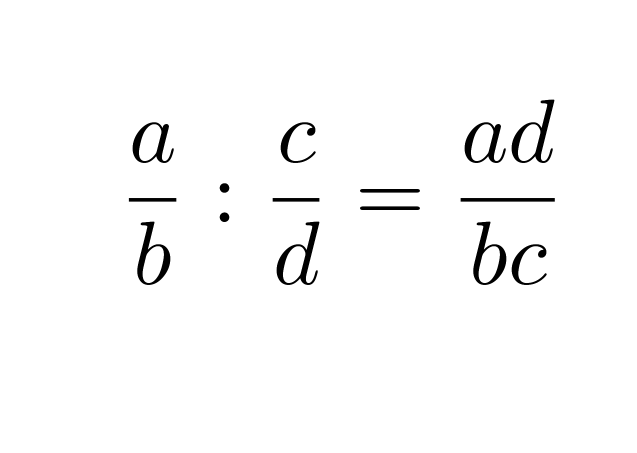
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
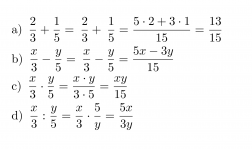
Klikkaa kuva suuremmaksi!
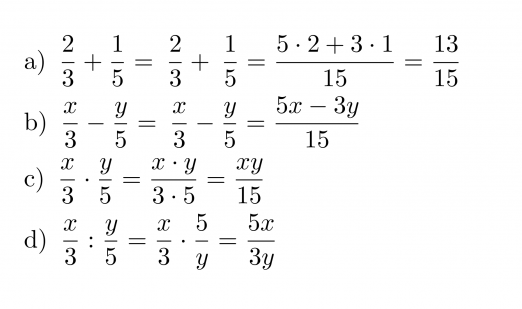
Klikkaa kuva suuremmaksi!
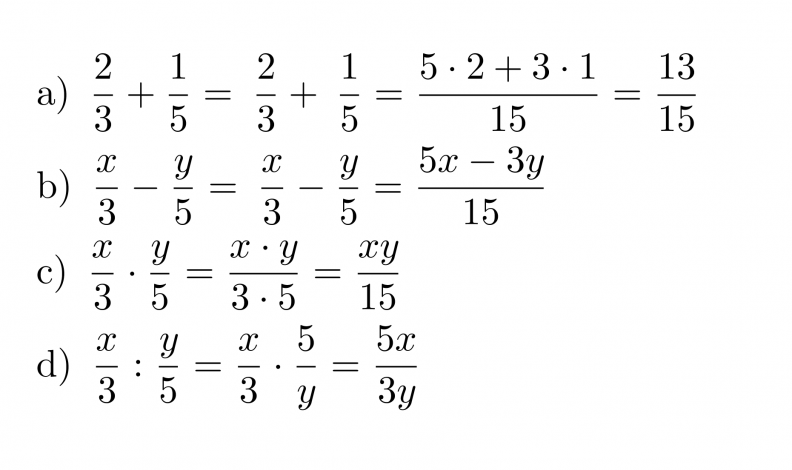
Klikkaa kuva suuremmaksi!
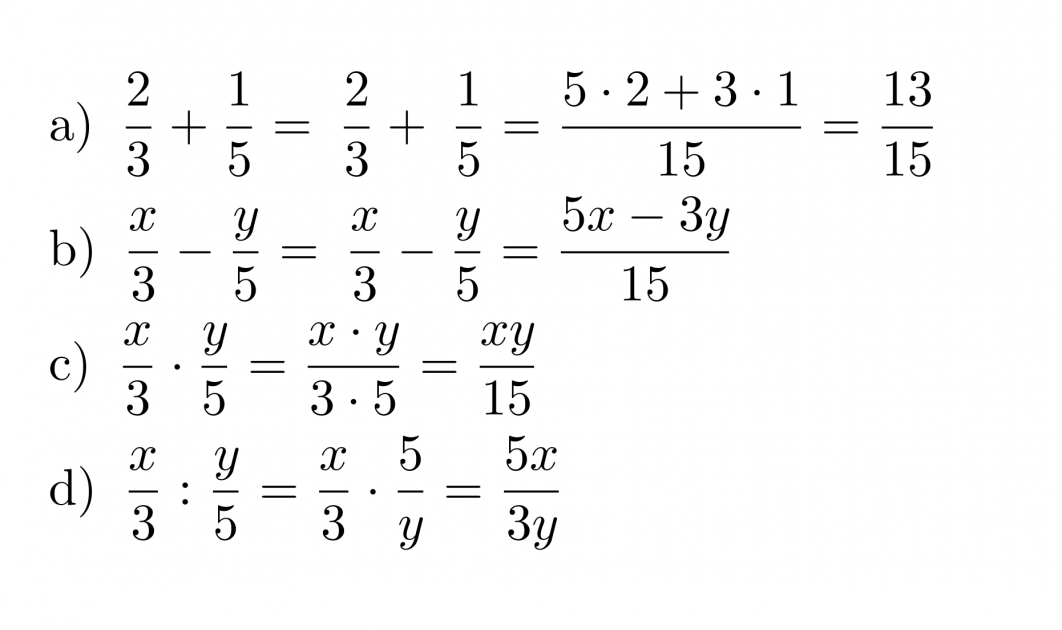
Klikkaa kuva suuremmaksi!
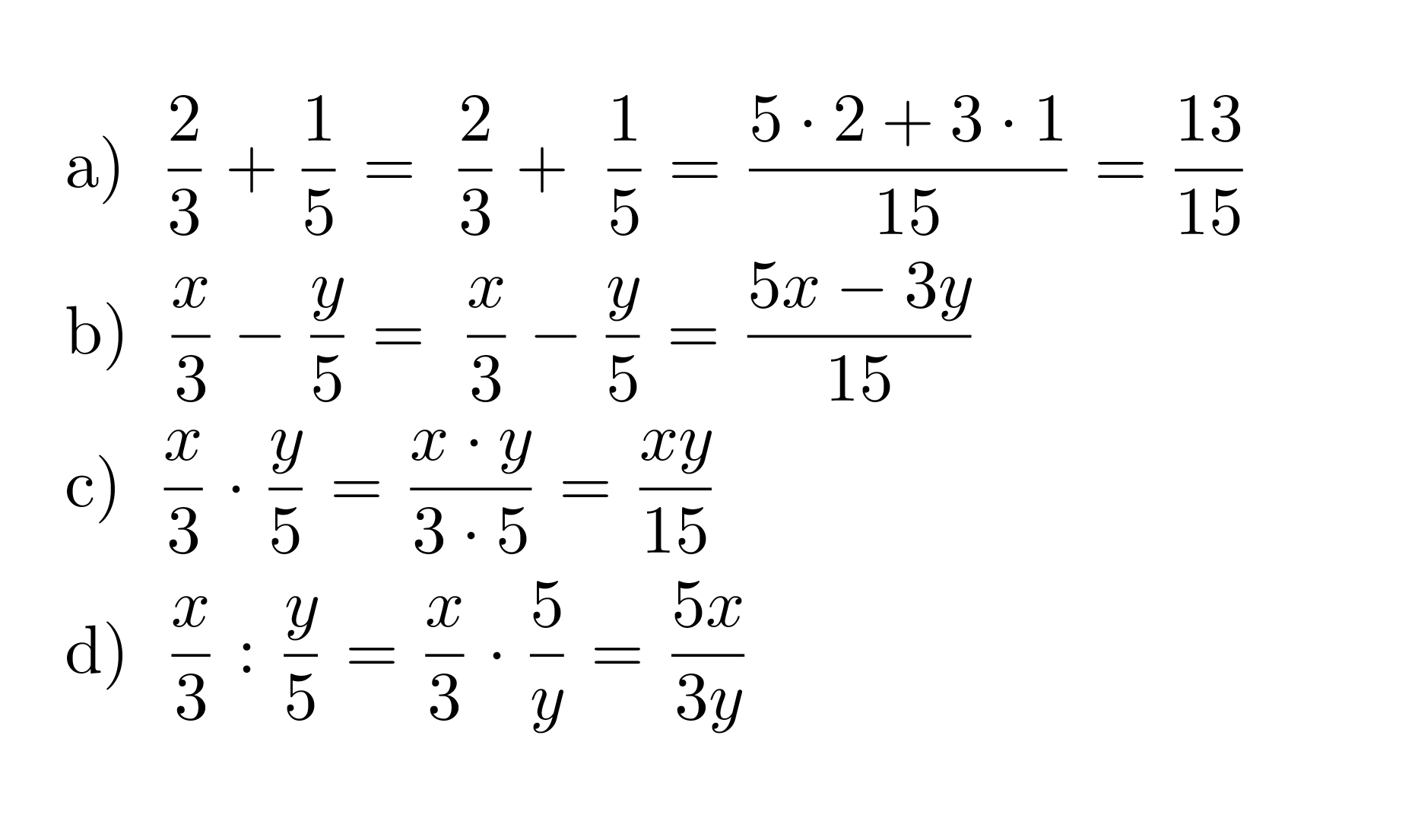
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
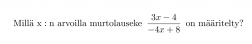
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
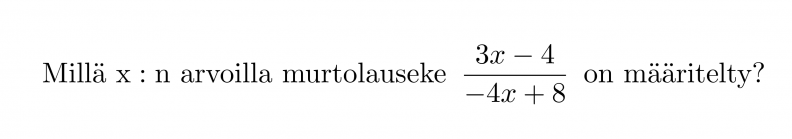
Klikkaa kuva suuremmaksi!
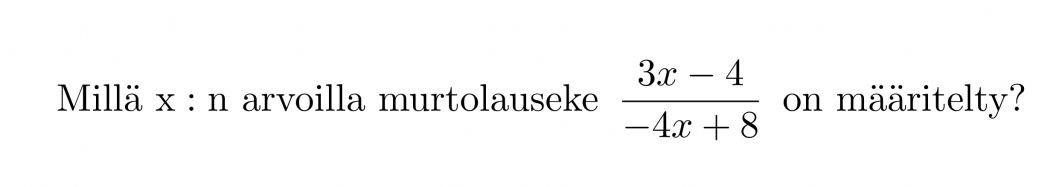
Klikkaa kuva suuremmaksi!
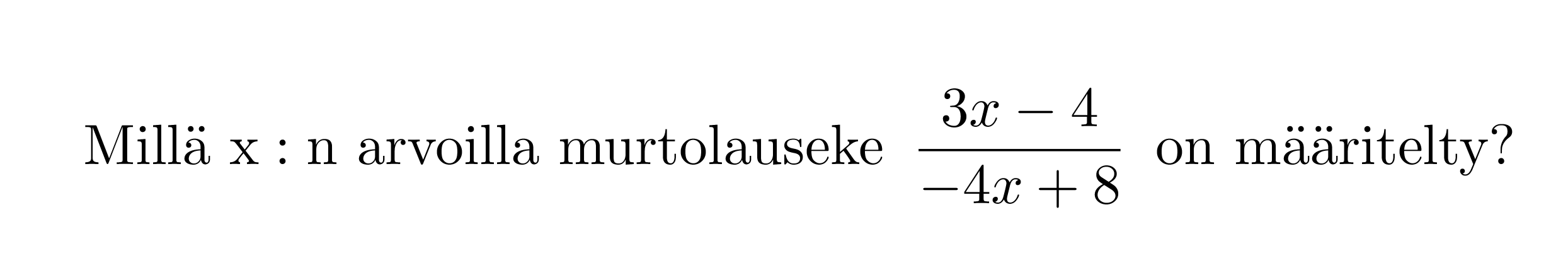
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
Murtolauseke on määritelty muualla paitsi nimittäjän nollakohdissa. Selvitetään nimittäjän nollakohta.
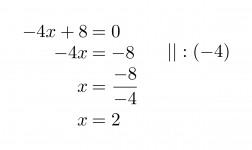
Klikkaa kuva suuremmaksi!
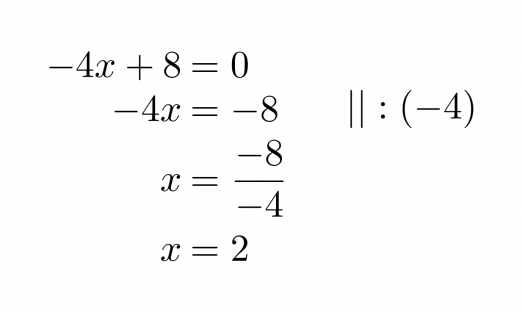
Klikkaa kuva suuremmaksi!
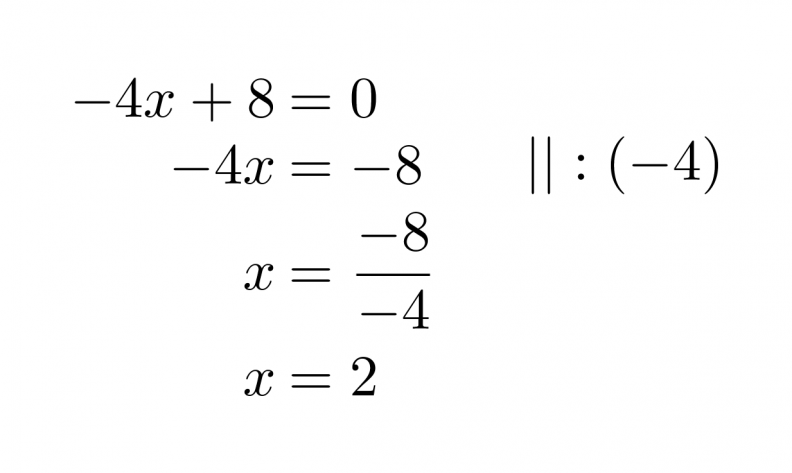
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
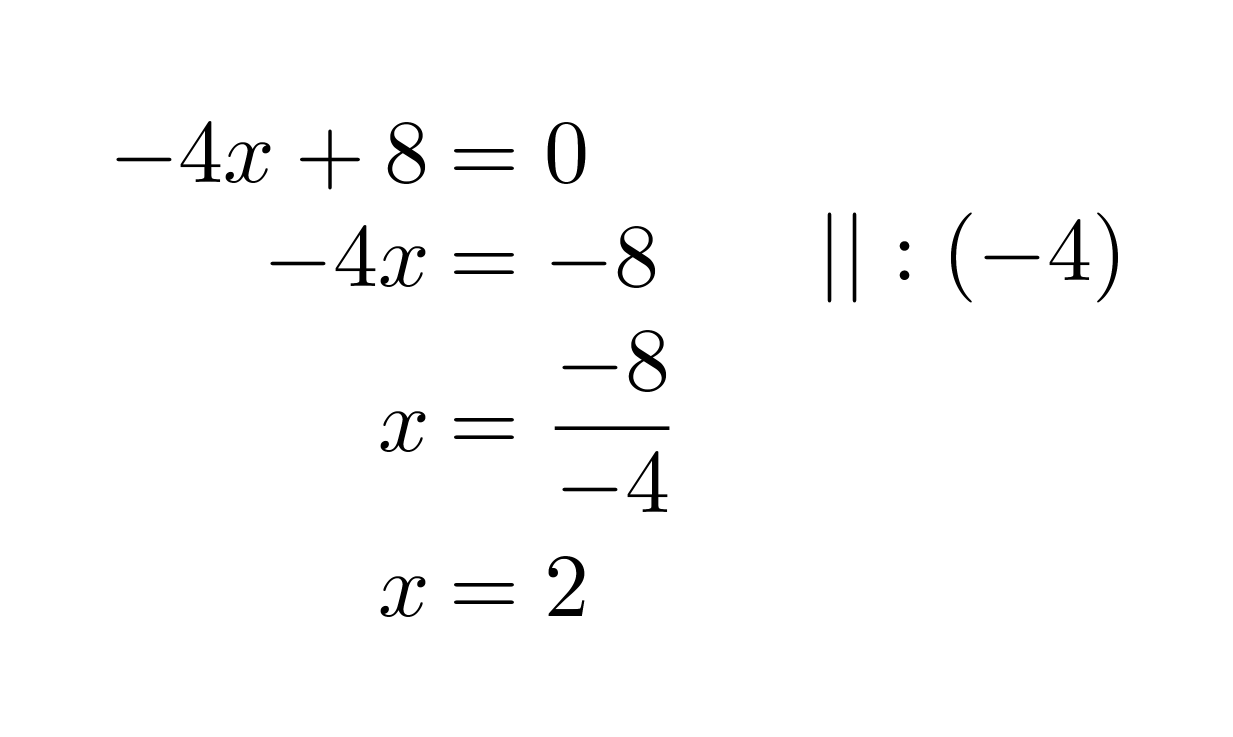
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Murtolauseke on määritelty, kun x ≠ 2.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014
Murtolausekkeiden laskusäännöt