10. Polynomin jakaminen monomilla ja polynomilla*
Kun polynomeja kerrotaan keskenään, on kaikki sulkeiden sisällä olevat termit kerrottava erikseen. Vastaavasti polynomin jakolaskussa on jokainen termi tultava jaetuksi erikseen.
Esimerkki 1.
Suoritetaan jakolasku.
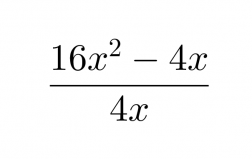
Klikkaa kuva suuremmaksi!
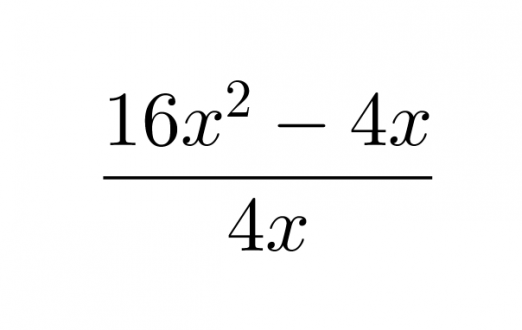
Klikkaa kuva suuremmaksi!
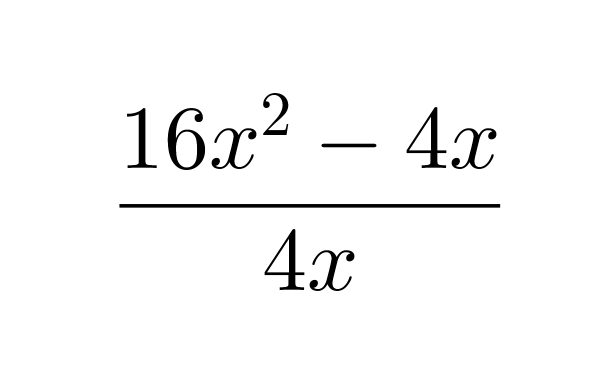
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tapa I
Jaetaan polynomin 16x2 – 4 jokainen termi erikseen monomilla 4x.
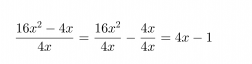
Klikkaa kuva suuremmaksi!
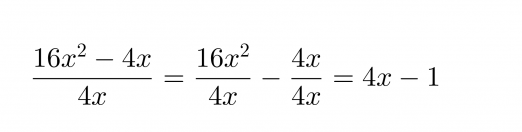
Klikkaa kuva suuremmaksi!
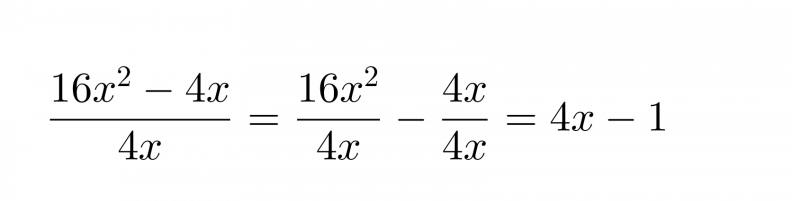
Klikkaa kuva suuremmaksi!
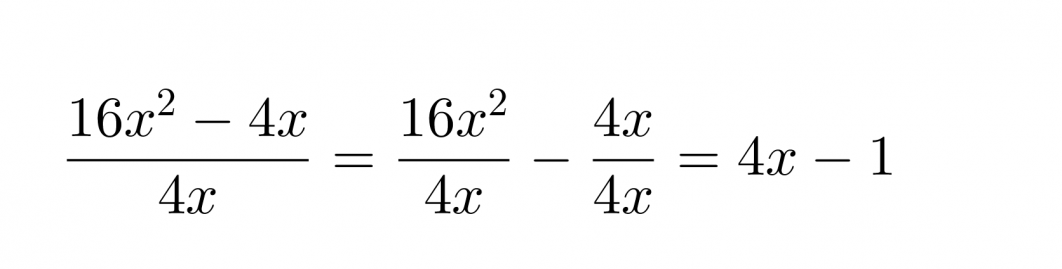
Klikkaa kuva suuremmaksi!
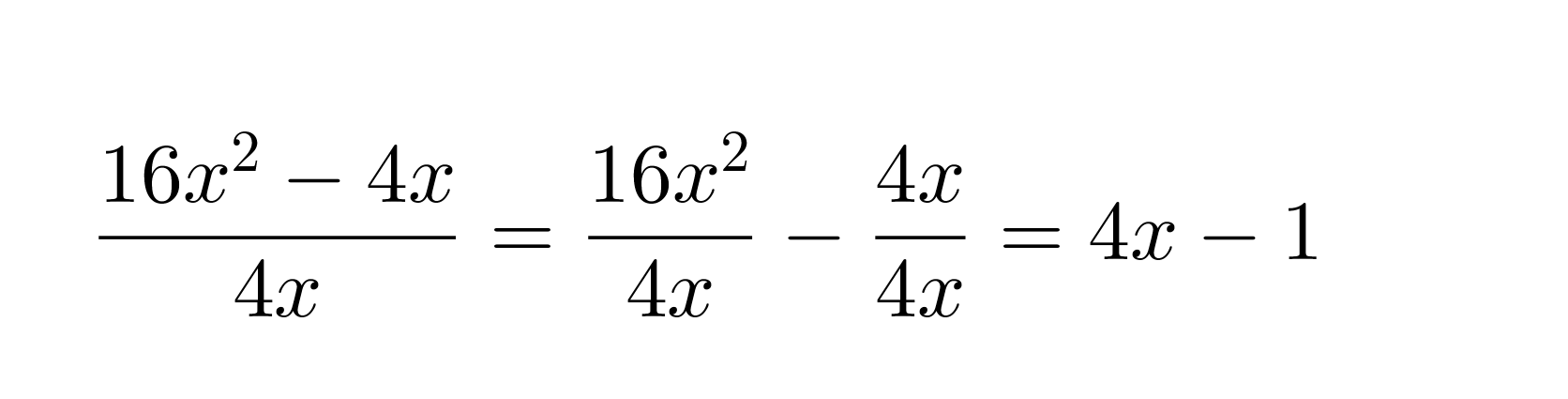
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tapa II
Jakolasku voidaan suorittaa myös siten, että jaettava muunnetaan ensin tulomuotoon ja sen jälkeen supistetaan osoittajan ja nimittäjän yhteisillä termeillä.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Jos jaettavana on tulomuotoinen polynomi, saa ainoastaan kertojan tai kerrottavan jakaa. Jos jakolasku tehtäisiin molempiin tekijöihin, tulisi jakolasku suoritettua kahdesti.
Jos polynomi jaetaan polynomilla, jossa on vähintään kaksi termiä, ei esimerkin 1 ensimmäistä ratkaisutapaa voida käyttää. Tällaisen murtolausekkeen sieventäminen vaatii aina osoittajan ja nimittäjän jakamista sellaisiin tulomuotoisiin osiin, jotka voidaan supistaa pois.
Yleisin virhe polynomeja sisältävien murtolausekkeiden sieventämisessä on summamuotoisesta polynomista yksittäisten termien poistaminen. Tällöin jakolaskua ei ole suoritettu jokaiseen jaettavan termiin.
SUMMASTA EI SAA SUPISTAA!
Esimerkki 2.
Kun polynomi jaetaan polynomilla, on lausekkeet muutettava ensin tulomuotoon.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Jos nimittäjän yhteiseksi tekijäksi olisi valittu –2, olisi välittömästi saatu nimittäjälle ja osoittajalle yhteinen tekijä.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014
Polynomin jakaminen monomilla