11. Murto- ja verrantomuotoisen yhtälön ratkaiseminen
Verrantomuotoisessa yhtälössä kaksi murtolauseketta on merkitty yhtä suuriksi. Murtoyhtälö on yhtälö, jossa tuntematon esiintyy nimittäjässä.
Yhtälöt, joissa esiintyy murtolauseke saadaan yleensä helpoiten ratkaistua ristiin kertomalla. Ristiin kertominen on sallittua ainoastaan yhtäsuuruusmerkin yli ja silloinkin ainoastaan, kun yhtälön molemmat puolet ovat joko tulo- tai osamäärämuodossa. Yhteen- ja vähennyslaskuja saa siis ainoastaan esiintyä osoittajassa, nimittäjässä tai sulkeiden sisällä.
Murtoyhtälön nimittäjän nollakohdat eivät kelpaa murtoyhtälön ratkaisuiksi, sillä nollalla ei voi jakaa. Tämän vuoksi ennen vastauksen antamista on tarkistettava, kelpaako saatu arvo ratkaisuksi.
Esimerkki 1.
Ratkaistaan verrantomuotoinen yhtälö
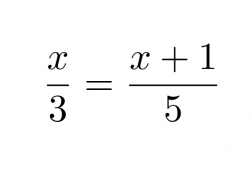
Klikkaa kuva suuremmaksi!
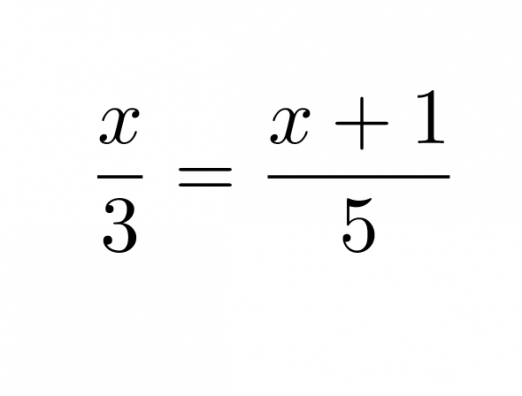
Klikkaa kuva suuremmaksi!
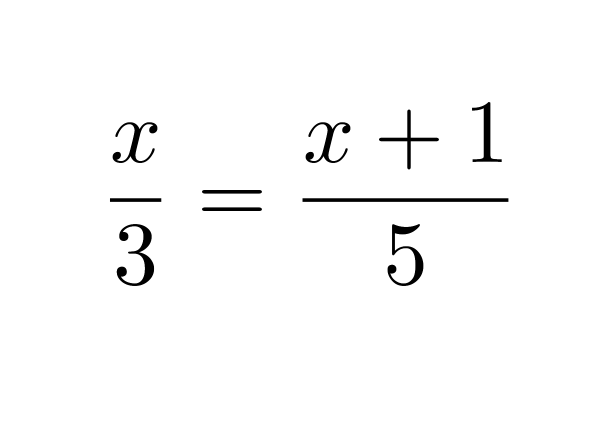
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Murtolausekkeista päästään eroon ristiin kertomalla.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: x = 3/2.
Esimerkki 2.
Ratkaistaan murtoyhtälö.
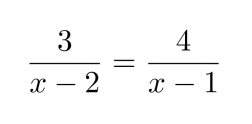
Klikkaa kuva suuremmaksi!
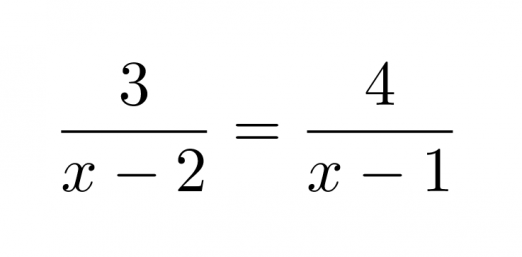
Klikkaa kuva suuremmaksi!
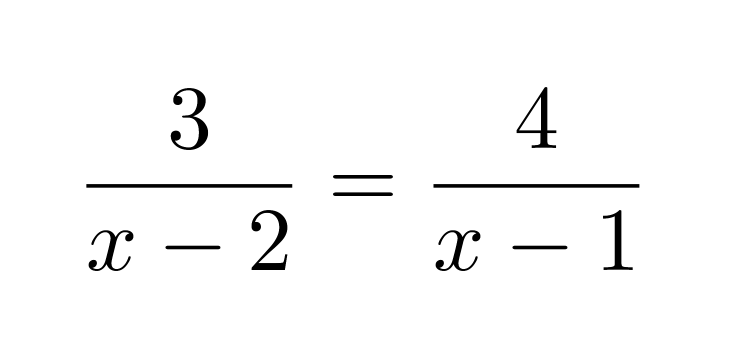
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Nimittäjien nollakohdat ovat x = 2 ja x = 1, joten yhtälö on määritelty, kun x ≠ 2 ja x ≠ 1.
Kerrotaan lausekkeet ristiin.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tämä kelpaa ratkaisuksi, sillä kumpikaan nimittäjistä ei saa tällöin arvoa nolla.
Vastaus: x = 5.
Esimerkki 3.
Ratkaistaan yhtälö.
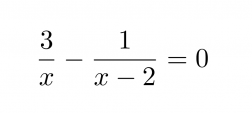
Klikkaa kuva suuremmaksi!
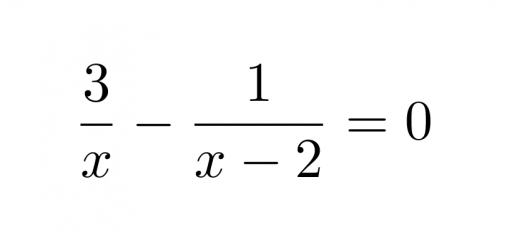
Klikkaa kuva suuremmaksi!
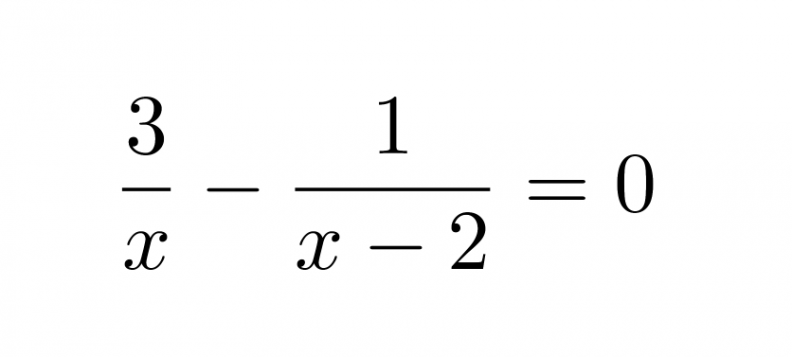
Klikkaa kuva suuremmaksi!
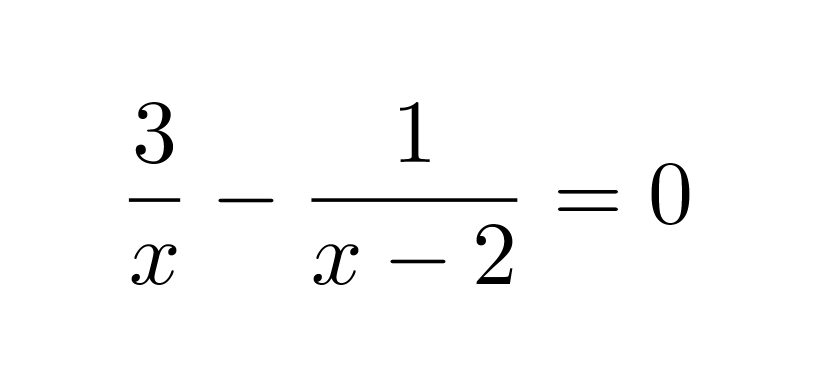
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Nimittäjien nollakohdat ovat x = 0 ja x = 2, joten yhtälö on määritelty, kun x ≠ 0 ja x ≠ 2.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: x = 6.
Esimerkki 4.
Ratkaistaan yhtälö

Klikkaa kuva suuremmaksi!
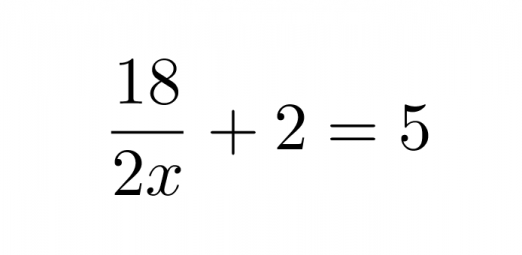
Klikkaa kuva suuremmaksi!
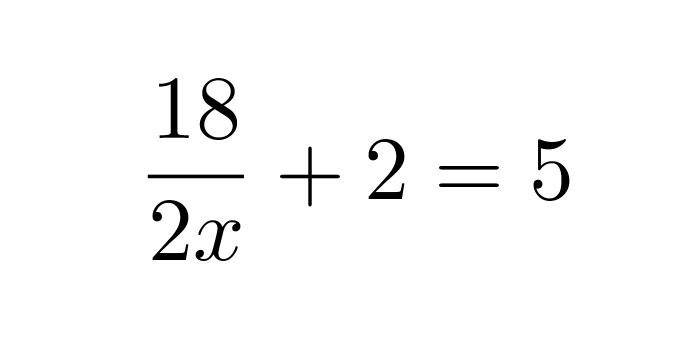
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Nimittäjän nollakohta on x = 0, joten yhtälö on määritelty, kun x ≠ 0.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tämä kelpaa ratkaisuksi.
Vastaus: x = 3.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014