12. Suoraan ja kääntäen verrannollisuus
Verrantoa voidaan hyödyntää useiden ongelmien ratkaisemisessa. Ennen kahden suureen verrannon muodostamista on pääteltävä, onko kysymyksessä suoraan- vai kääntäen verrannollisuus. Suoraan verrannolliset suureet muuttuvat samassa suhteessa ja niitä voidaan havainnollistaa origon kautta kulkevalla suoralla.
Jos suureet x ja y ovat suoran verrannolliset, toteuttavat niiden lukuparit (x1, y1) ja (x2, y2) verrannon
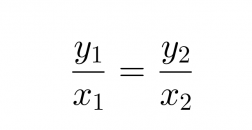
Klikkaa kuva suuremmaksi!
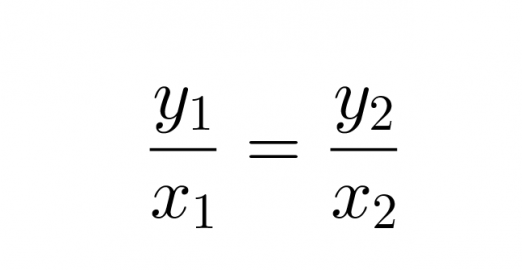
Klikkaa kuva suuremmaksi!
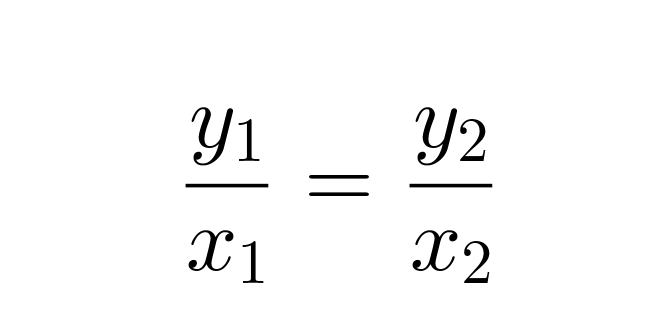
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tämä voidaan kirjoittaa myös muodossa:
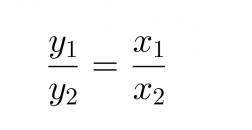
Klikkaa kuva suuremmaksi!
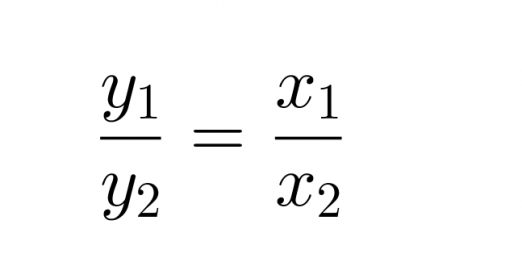
Klikkaa kuva suuremmaksi!
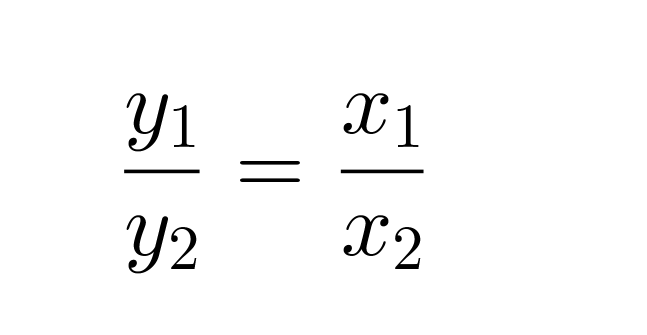
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kääntäen verrannolliset suureet muuttuvat niin, että toisen kasvaessa toinen pienenee. Suureiden tulo pysyy kuitenkin suureiden muuttuessa aina samana.
Jos suureet x ja y ovat kääntäen verrannolliset, toteuttavat niiden lukuparit (x1, y1) ja (x2, y2) yhtälön x1, y1 = x2, y2.
Tämä voidaan kirjoittaa myös muodossa:
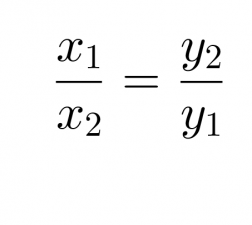
Klikkaa kuva suuremmaksi!
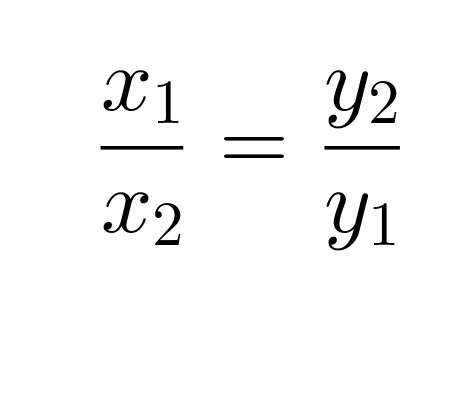
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Sijoitettaessa suureen arvoja verrantoon on tärkeää, että ne sijoitetaan laatuineen. Tällaisella suurelaskennalla on se etu, että tuloksen laadusta voidaan jo päätellä, onko tulos oikein.
Esimerkki 1.
Susannelta kului viiden kilometrin matkan rullaluistelemiseen 12 min. Kauanko häneltä kesti 23 km matkan luisteleminen? Oletetaan hänen luistelevan samalla nopeudella.
Ratkaisu:
Verrannon muodostamisessa voidaan käyttää hyväksi asetelmaa. Merkitään kysyttyä aikaa x:llä ja päätellään kasvaako vai pieneneekö käytetty aika matkan kasvaessa.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koska nuolet ovat samansuuntaisia, on kyseessä suoraan verrannolliset suureet. Kun verranto muodostetaan asetelman pohjalta, on yhtälön molemmilla puolilla olevien nuolien oltava samansuuntaiset.
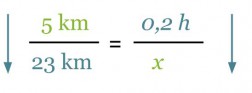
Klikkaa kuva suuremmaksi!
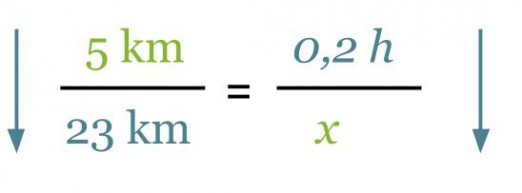
Klikkaa kuva suuremmaksi!
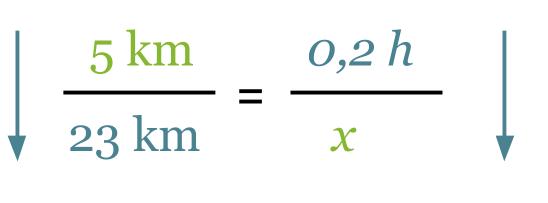
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaistaan yhtälö suorittamalla aluksi ristiin kertominen.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Susanne luistelee 23 km 55 minuutissa.
Esimerkki 2.
Jos Susanne luistelee nopeudella 20 km/h, matka kotoa mummolaan kestää 45 min. Paljonko aikaa sääsyy, jos hänen nopeutensa olisi 25 km/h?
Ratkaisu:
Ratkaistaan aluksi kauanko aikaa kuluu matkaan nopeudella 25 km/h. Merkitään matkaan kuluvaa aikaa x:llä ja laaditaan asetelma nopeuksista ja ajoista. Mitä suuremmalla nopeudella mennään, sitä vähemmän aikaa kuluu samanmittaiseen matkaan. Laskuissa on käytettävä samoja yksiköitä, joten muutetaan aika tunneiksi.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koska nuolet ovat erisuuntaisia on kyseessä kääntäen verrannolliset suureet. Jotta asetelmasta voitaisiin muodostaa verranto, on toinen nuolista ”käännettävä” samansuuntaiseksi
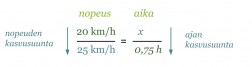
Klikkaa kuva suuremmaksi!
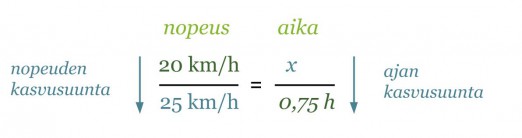
Klikkaa kuva suuremmaksi!
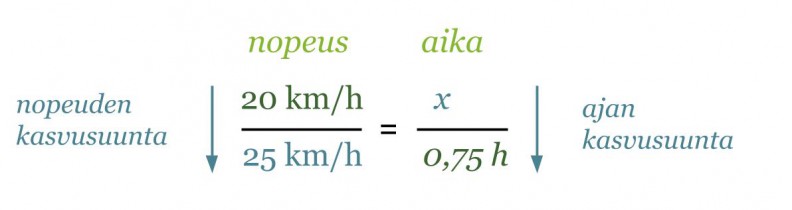
Klikkaa kuva suuremmaksi!
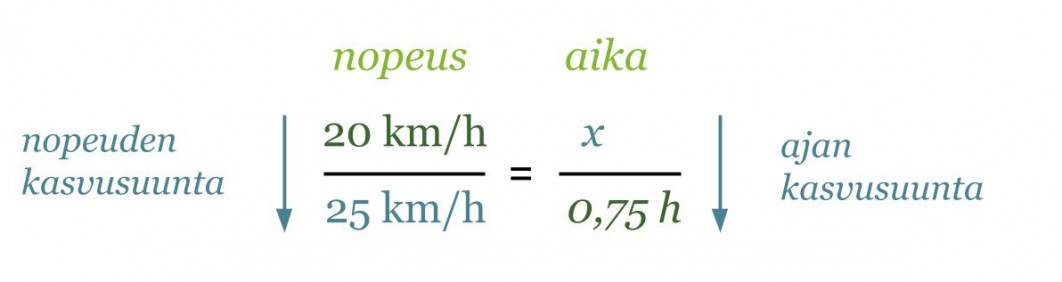
Klikkaa kuva suuremmaksi!
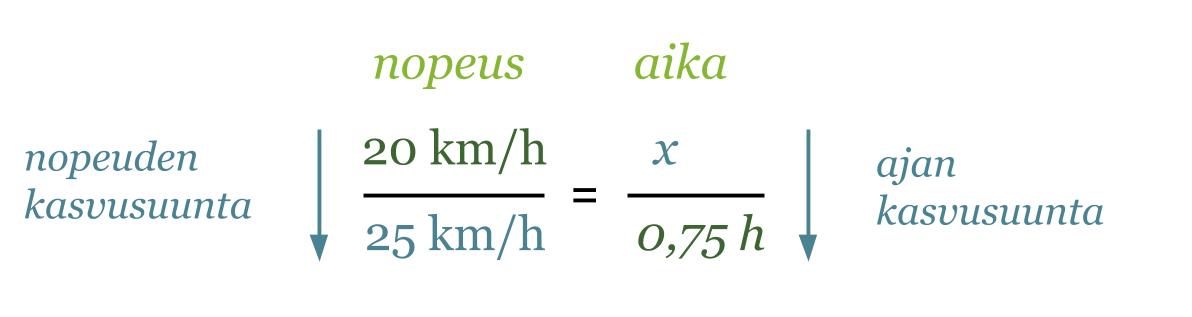
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaistaan yhtälö suorittamalla aluksi ristiin kertominen.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Aikojen erotukseksi saadaan 45 min – 36 min = 9 min.
Vastaus: Nopeudella 25 km/h matka kestää 9 minuuttia vähemmän.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014