13. Potenssit ja juuret
Potenssi on kertolaskun lyhennetty merkintätapa silloin, kun samaa lukua kerrotaan itsellään useamman kerran.
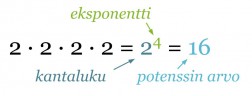
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
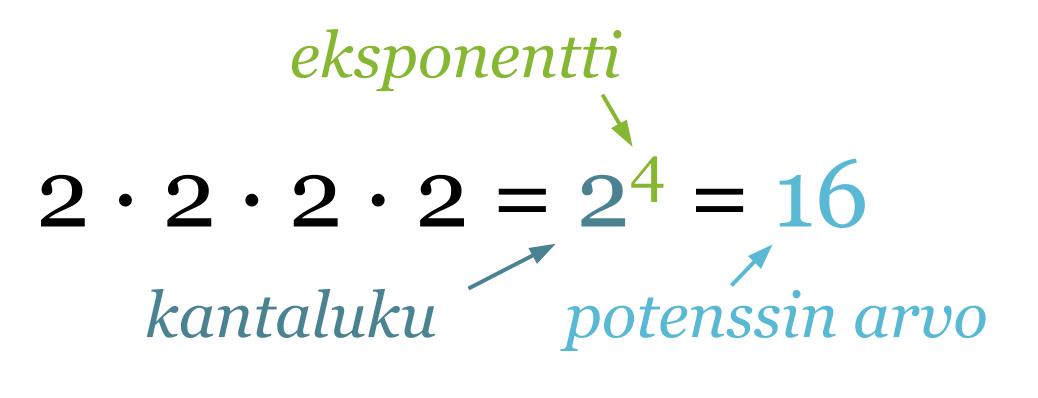
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Potenssin kantaluvun kanssa on oltava tarkkana. Jos sulkeita ei käytetä, eksponentti vaikuttaa vain siihen lukuun, joka on suoraan eksponentin alla.
Jos eksponenttina on nolla, on potenssin arvo aina 1. Kantalukuna ei kuitenkaan saa olla nolla.
a0 = 1, kun a≠ 0.
Suuret ja pienet luvut merkitään yleensä havainnollisuuden vuoksi kymmenpotenssimuodossa a · 10n, missä kerroin a on yhden ja kymmenen välillä.
Potenssin negatiivinen eksponentti tarkoittaa kantaluvun käänteisluvun vastaavaa positiivista potenssia.
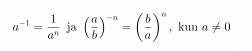
Klikkaa kuva suuremmaksi!
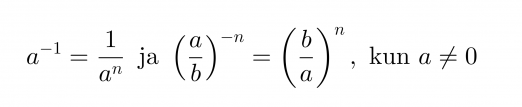
Klikkaa kuva suuremmaksi!
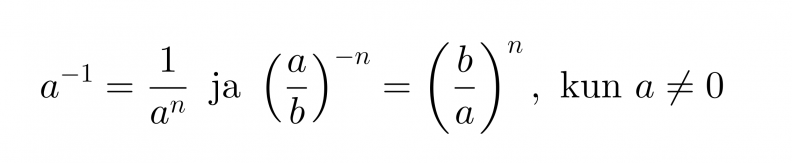
Klikkaa kuva suuremmaksi!
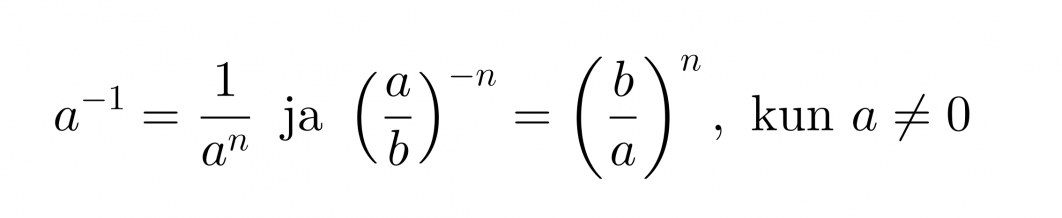
Klikkaa kuva suuremmaksi!
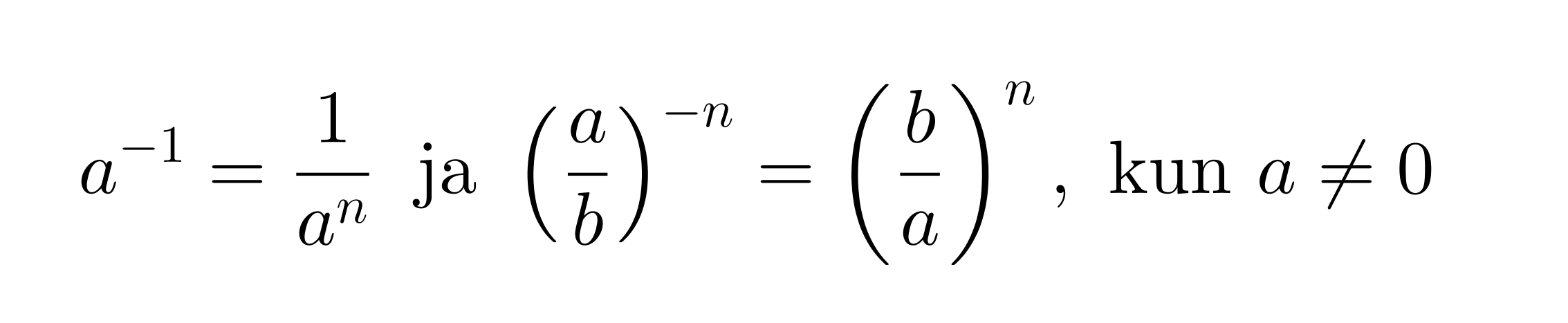
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jos positiivisen kantaluvun eksponenttina on murtoluku, voidaan sama merkitä myös juurimerkinnän avulla.
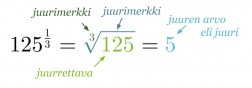
Klikkaa kuva suuremmaksi!
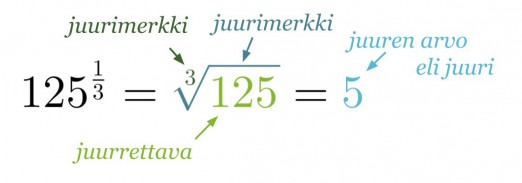
Klikkaa kuva suuremmaksi!
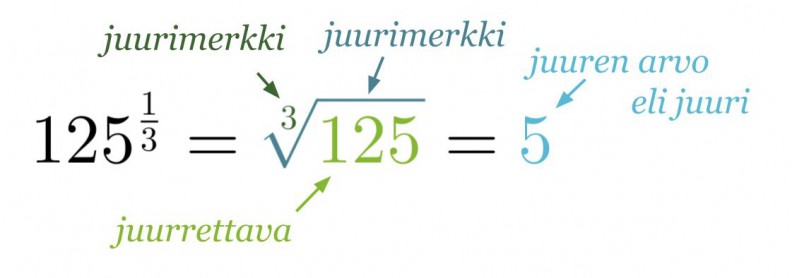
Klikkaa kuva suuremmaksi!
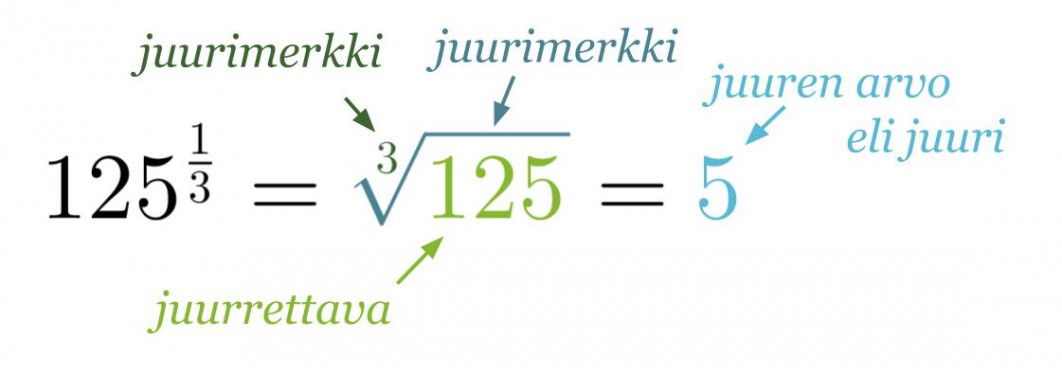
Klikkaa kuva suuremmaksi!
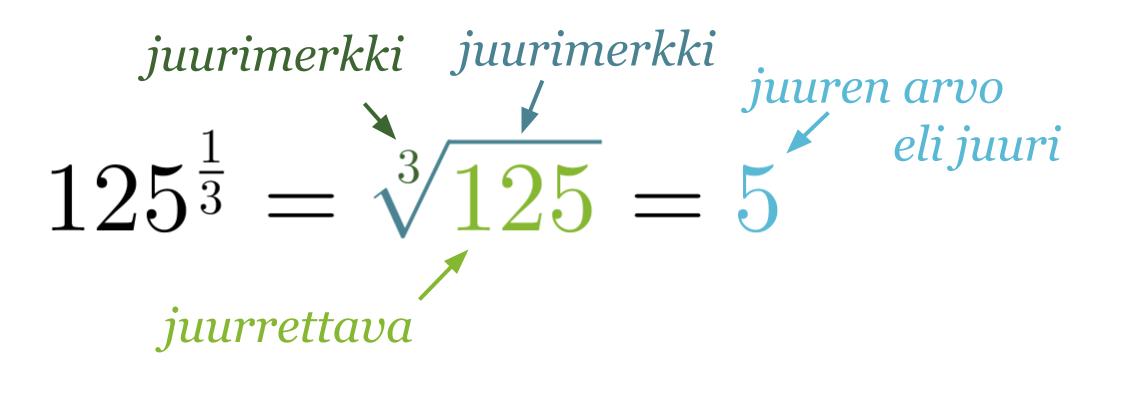
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Jos indeksi on luku 2, sitä ei merkitä näkyviin.
Olkoon n positiivinen kokonaisluku ja a > 0. Tällöin
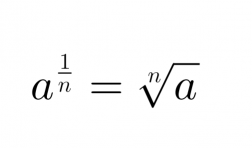
Klikkaa kuva suuremmaksi!
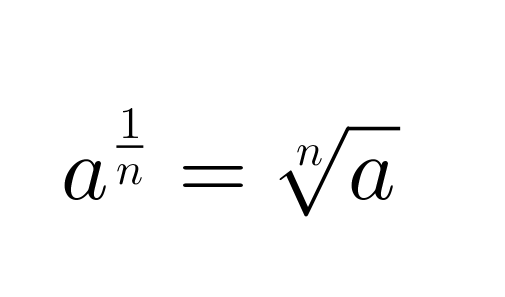
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Potenssien laskusäännöt löytyvät kirjan taulukko-osiosta. Näitä tarvitaan etenkin sellaisten potenssilausekkeiden sieventämisessä, jotka sisältävät muuttujia. Laskusäännöt ovat voimassa sekä positiivisille että negatiivisille eksponenteille. Jos laskusääntöjä sovelletaan silloin, kun eksponenttina on murtoluku, on kantaluvun oltava positiivinen.
Esimerkki 1.
Esitetään luvut ilman kymmenenpotenssia.
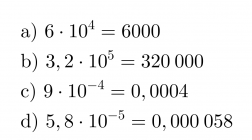
Klikkaa kuva suuremmaksi!
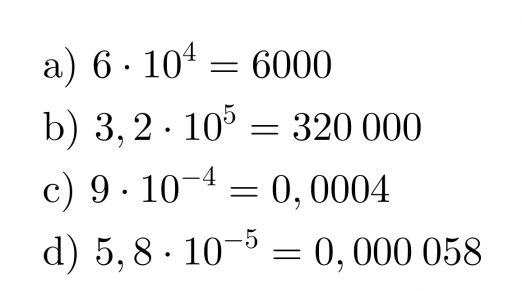
Klikkaa kuva suuremmaksi!
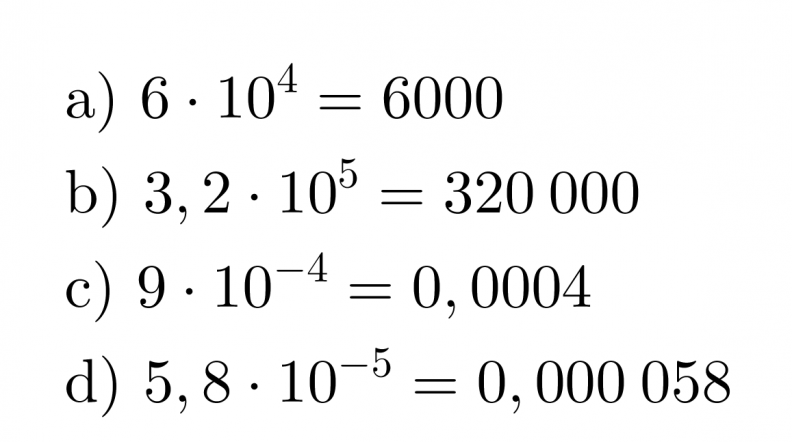
Klikkaa kuva suuremmaksi!
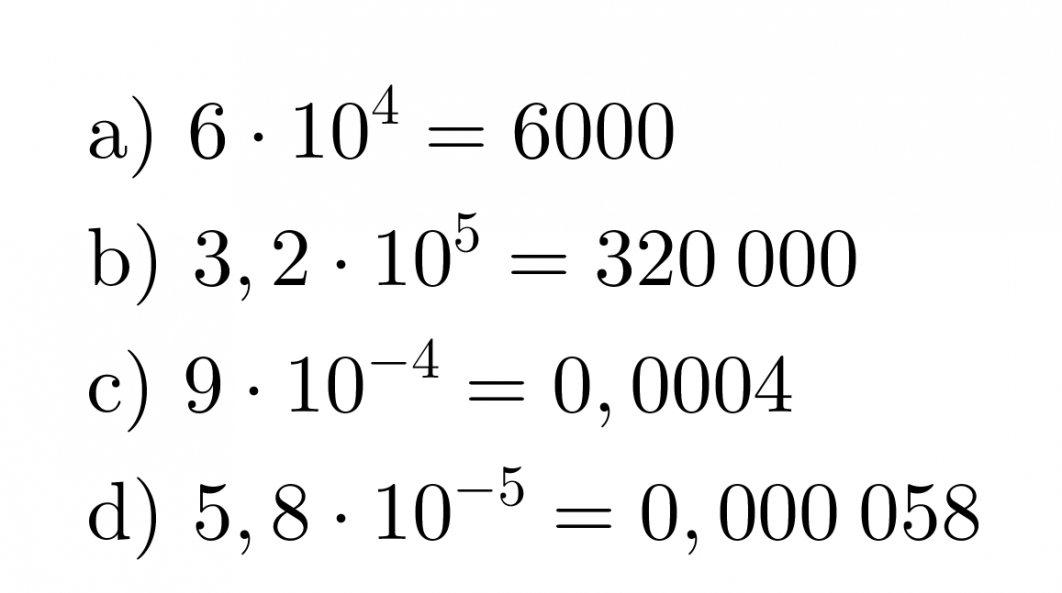
Klikkaa kuva suuremmaksi!
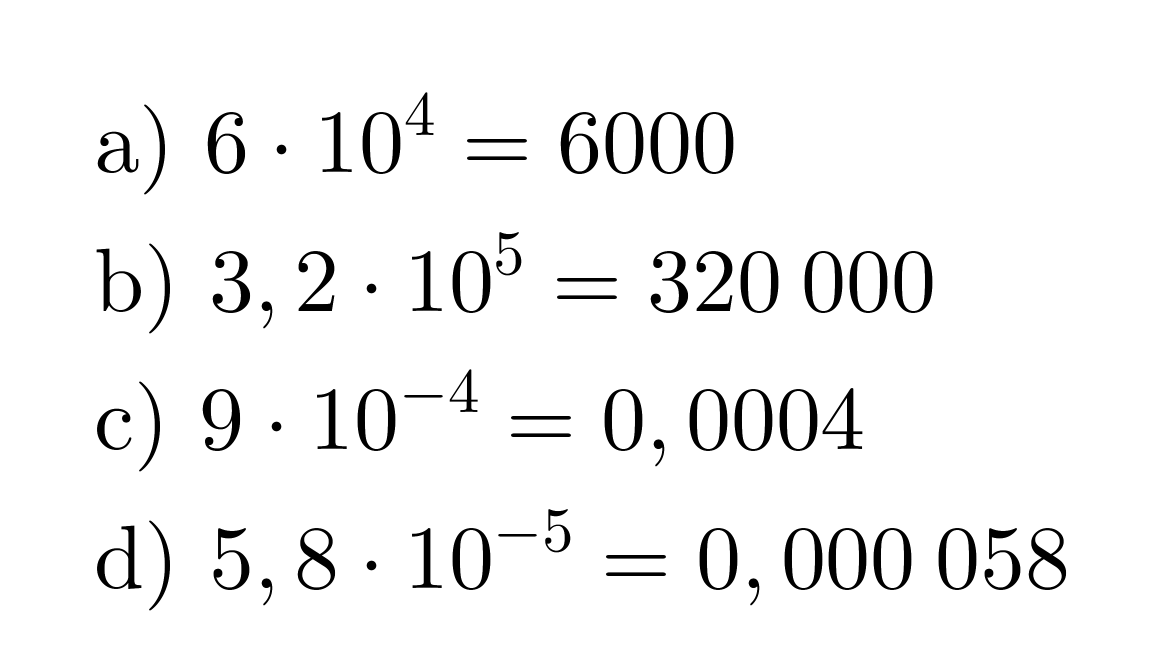
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Sievennetään potenssin laskusääntöjä käyttäen.
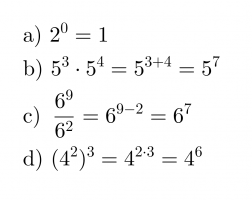
Klikkaa kuva suuremmaksi!
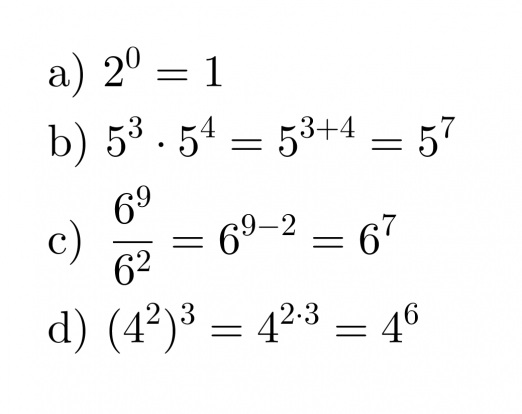
Klikkaa kuva suuremmaksi!
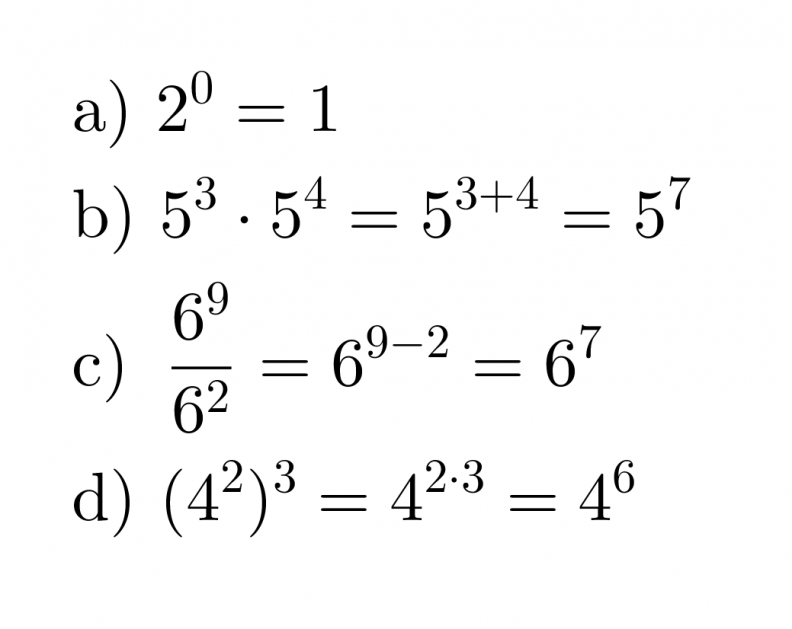
Klikkaa kuva suuremmaksi!
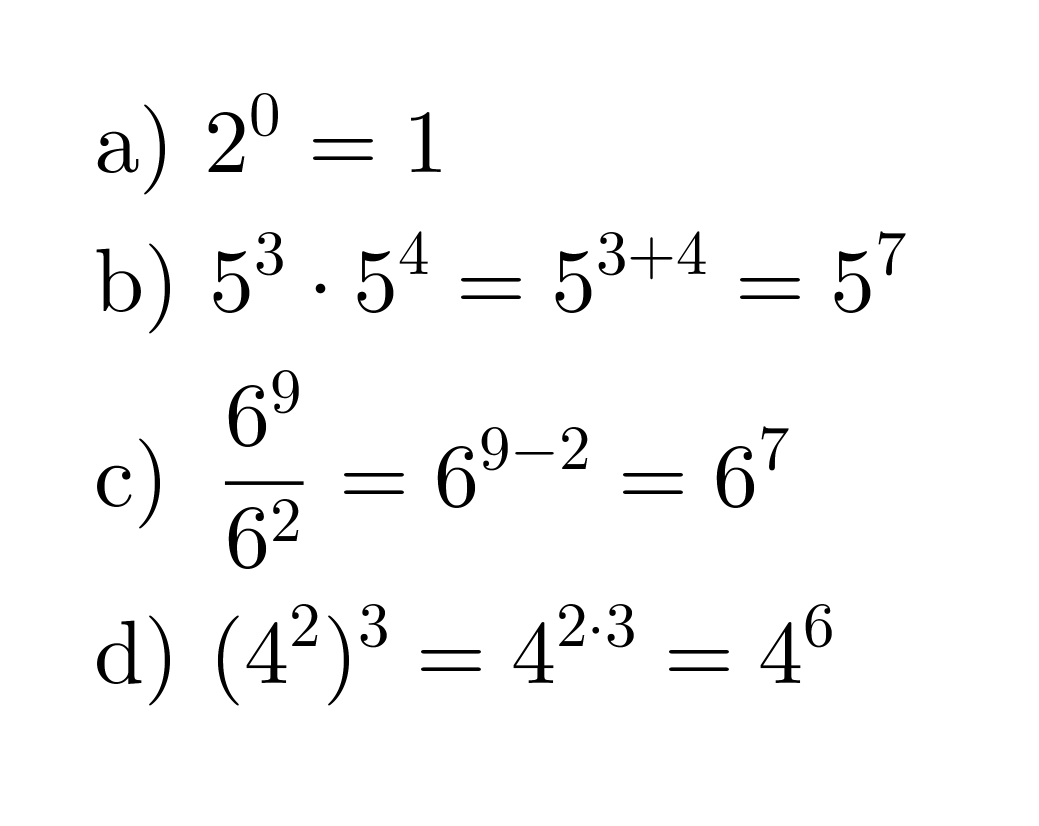
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
Sievennetään negatiiviset potenssit.

Klikkaa kuva suuremmaksi!
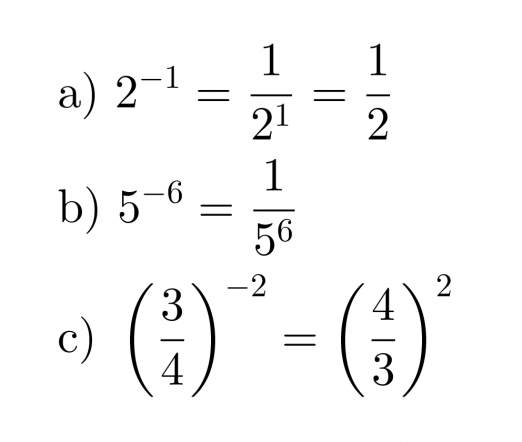
Klikkaa kuva suuremmaksi!
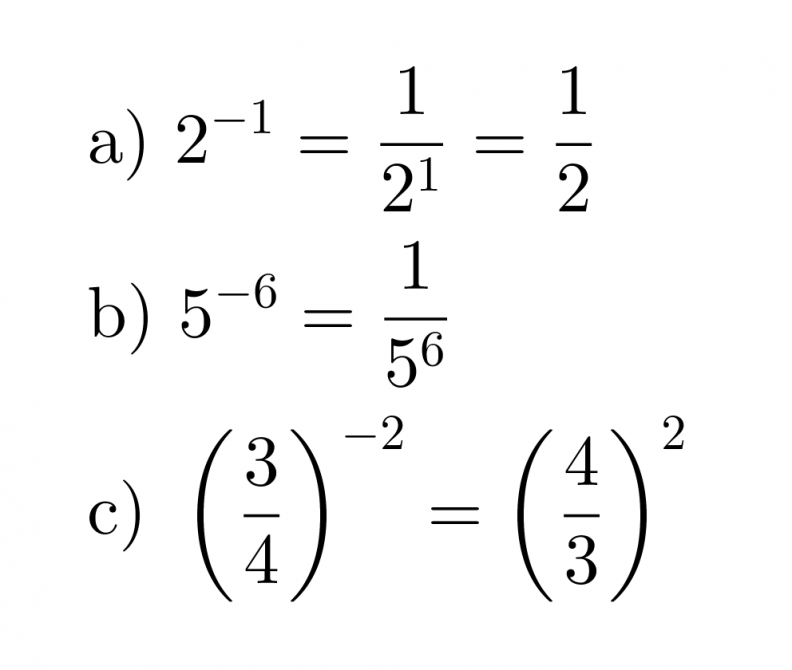
Klikkaa kuva suuremmaksi!
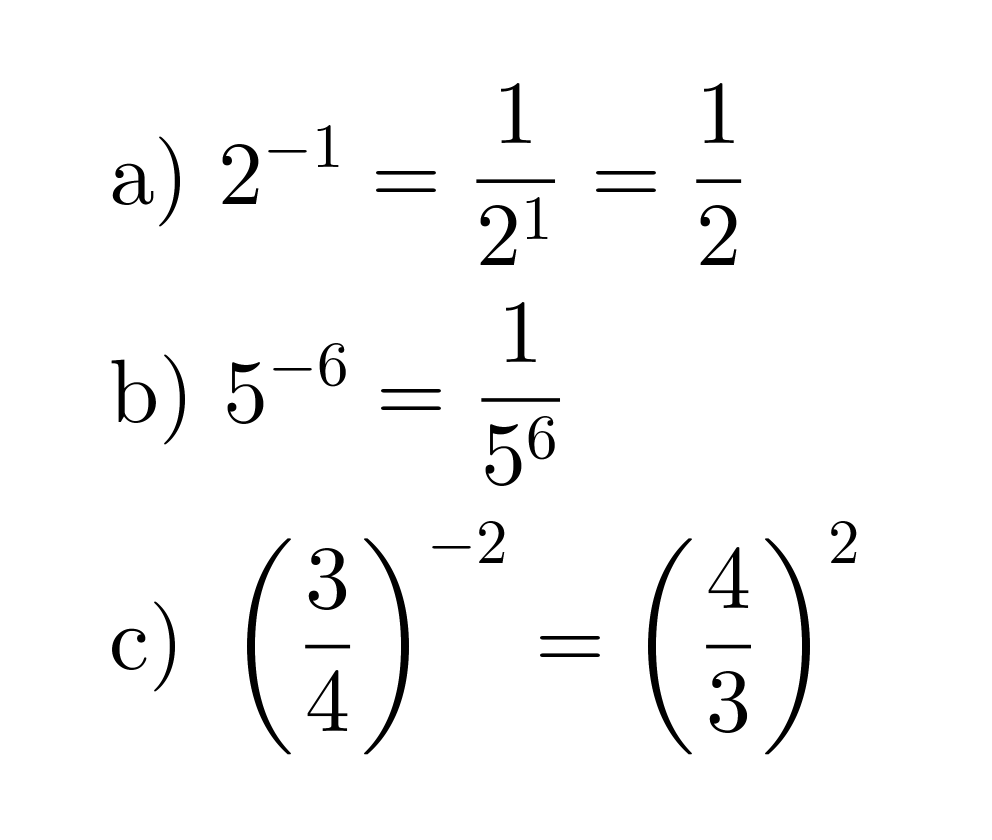
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 4.
Sievennetään murtopotenssit.
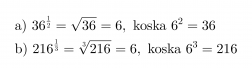
Klikkaa kuva suuremmaksi!
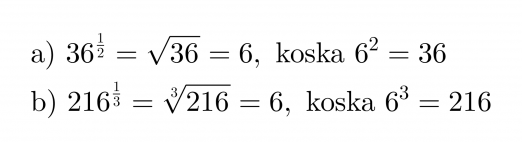
Klikkaa kuva suuremmaksi!
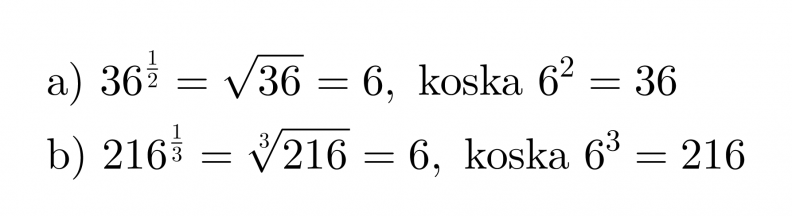
Klikkaa kuva suuremmaksi!
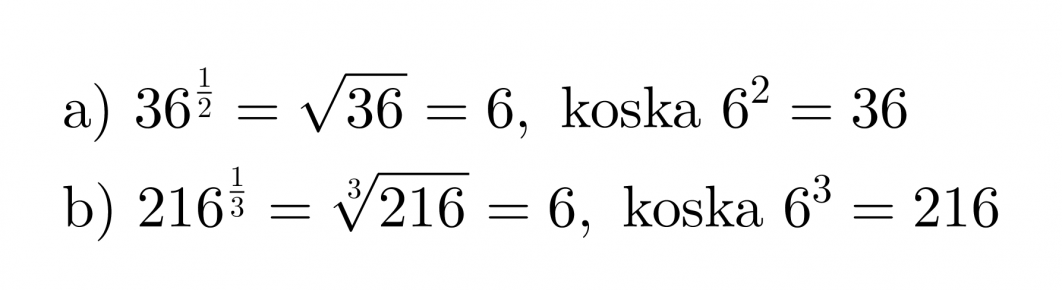
Klikkaa kuva suuremmaksi!
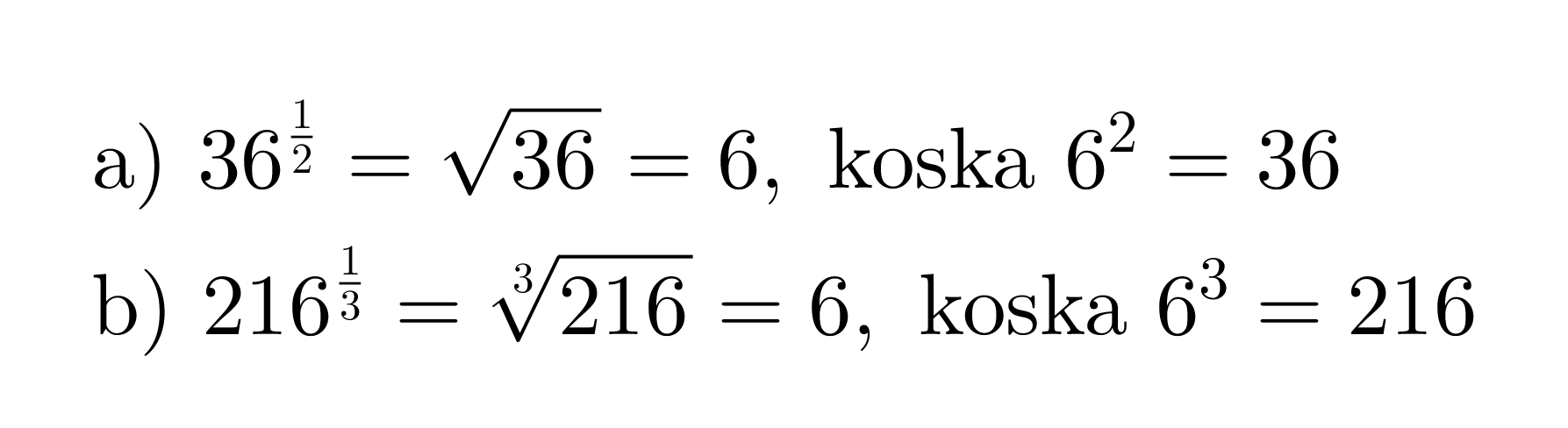
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 5.
Sievennetään juurilausekkeet.
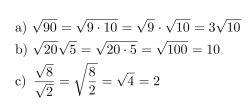
Klikkaa kuva suuremmaksi!
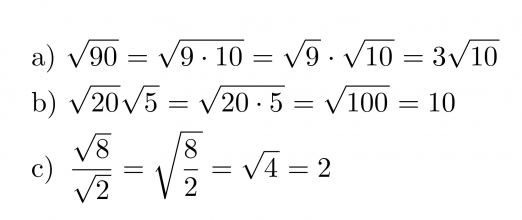
Klikkaa kuva suuremmaksi!
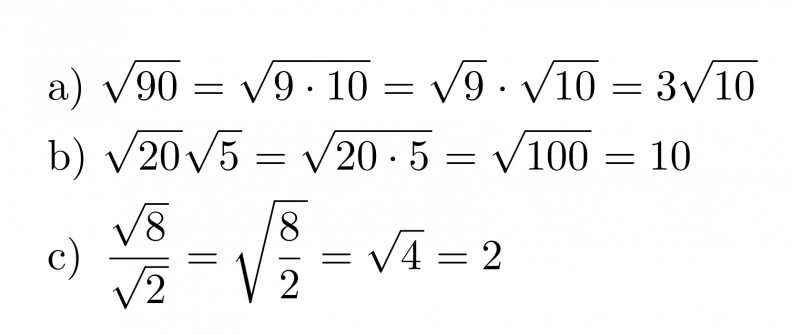
Klikkaa kuva suuremmaksi!
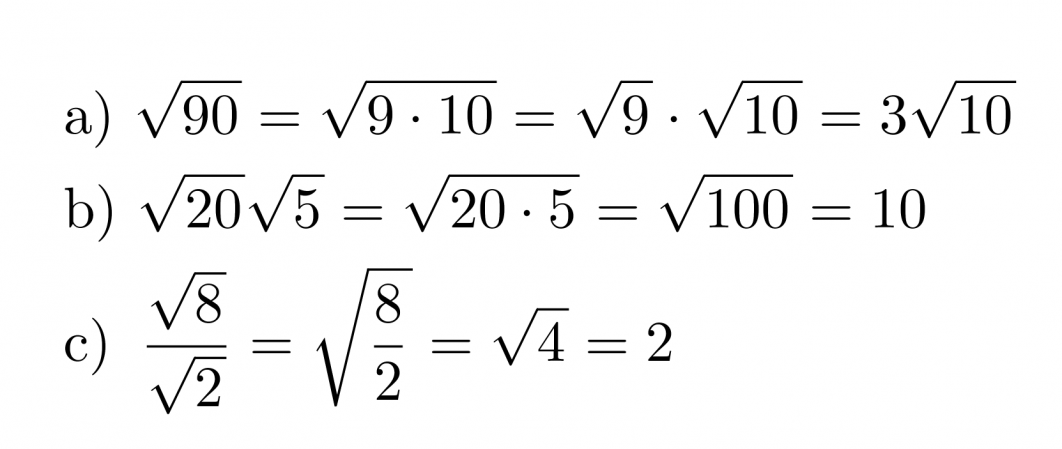
Klikkaa kuva suuremmaksi!
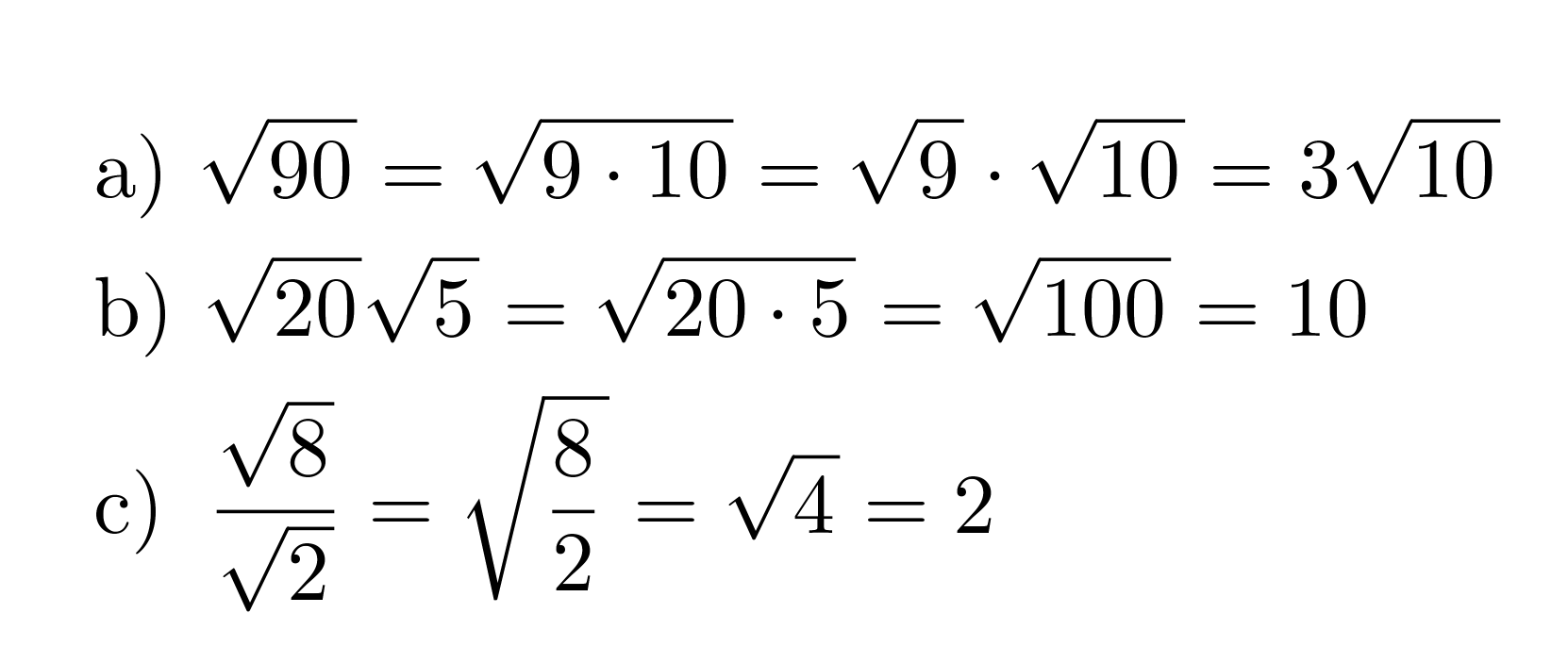
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!