14. Prosentti- ja promillelaskentaa
Suhteelliset osuudet ilmaistaan yleensä sadasosina eli prosentteina. Osuudet saadaan tällöin havainnollisiksi ja vertailukelpoisiksi.
Prosentti on sadasosa.
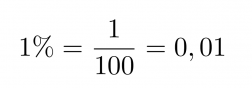
Klikkaa kuva suuremmaksi!
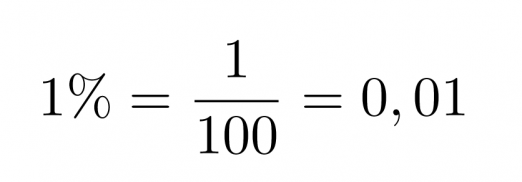
Klikkaa kuva suuremmaksi!
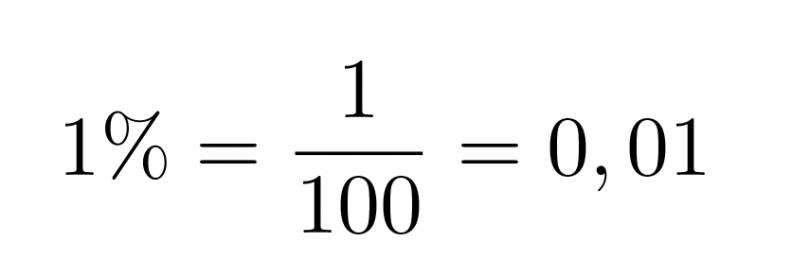
Klikkaa kuva suuremmaksi!
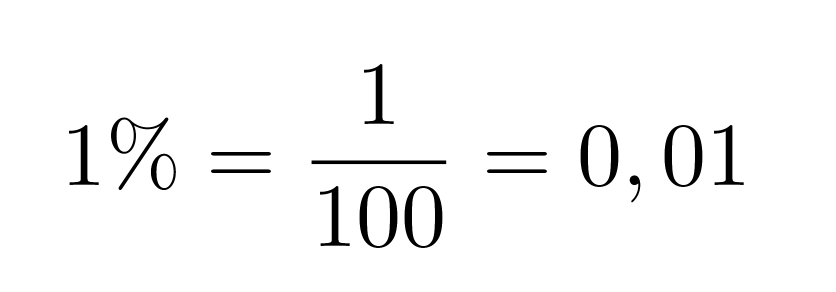
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jos prosenttiluvut tulevat kovin pieniksi, voidaan suhteet ilmaista myös promilleina, 10 promillea = 1 prosentti. Promilleina ilmaistaan veren alkoholipitoisuutta, jalometalliseosten pitoisuuksia jne.
Promille on tuhannesosa.
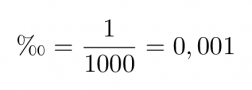
Klikkaa kuva suuremmaksi!
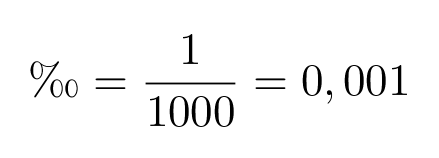
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Perusarvoksi kutsutaan sitä lukua, josta prosentti otetaan. Perusarvon valinnassa pitää olla tarkkana. Perusarvona on yleensä alkuperäinen arvo, esim. vanha hinta, johon vertailu kohdistuu. Kemian seoslaskuissa perusarvona on koko seoksen määrä.
Prosenttiosuus a/b sadasosiksi muutettuna kertoo, kuinka monta prosenttia luku a on luvusta b.
Edellisessä määritelmässä luku b kuvaa perusarvoa. Mitä voit sanoa perusarvosta seuraavassa määritelmässä?
Kun lasketaan, kuinka paljon on p % luvusta a, niin p % ilmaistaan desimaalilukuna, jolla kerrotaan luku a.
Esimerkki 1.
Henkilön veren alkoholipitoisuus on 3 ‰. Tämä tarkoittaa puhtaan alkoholin osuutta ihmisen verimäärää kohden. Lasketaan, paljonko henkilön veressä on puhdasta alkoholia, kun hänessä on verta 4700 grammaa.
0,003 · 4700 g = 14,2 g
Vastaus: Veressä on 14,2 g alkoholia.
Esimerkki 2.
200 grammaa 15-prosenttista ja 100 grammaa 40-prosenttista rikkihappoa sekoitetaan keskenään. Lasketaan kuinka moniprosenttista rikkihappoa saadaan.
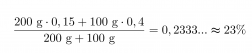
Klikkaa kuva suuremmaksi!
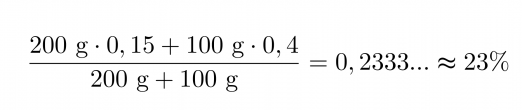
Klikkaa kuva suuremmaksi!
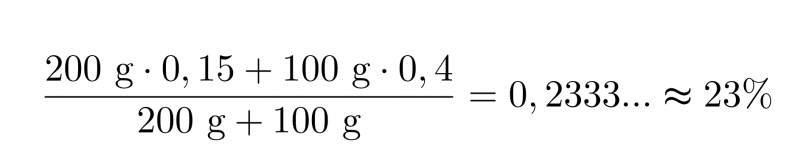
Klikkaa kuva suuremmaksi!
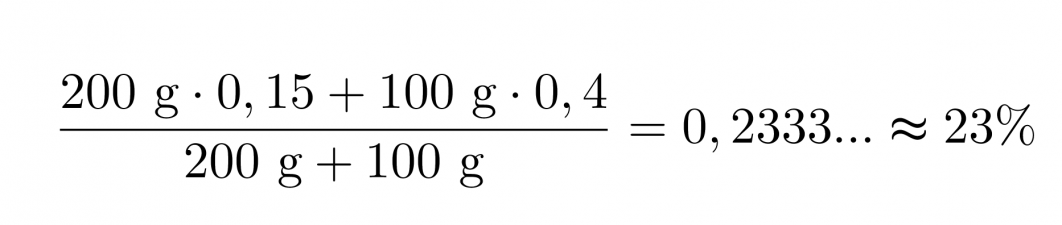
Klikkaa kuva suuremmaksi!
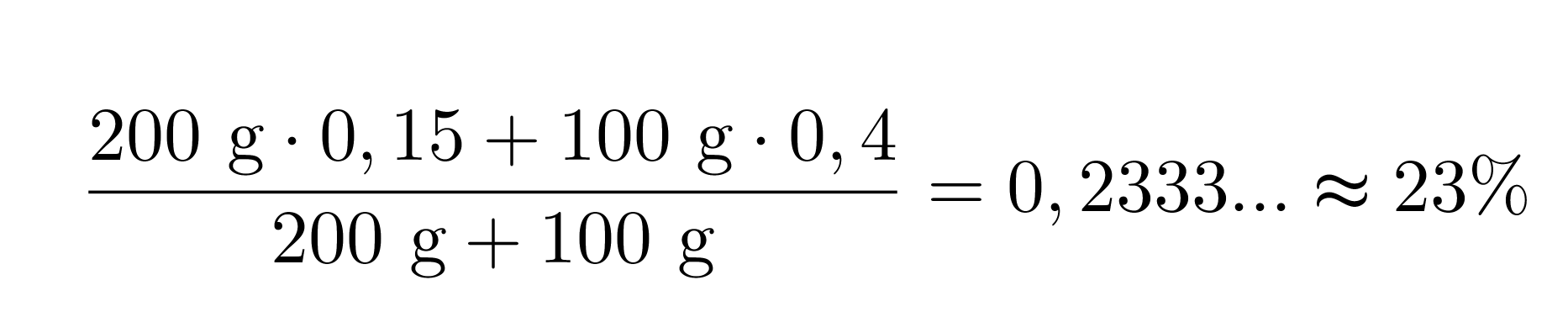
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Saadaan 23 prosenttista rikkihappoa.
Esimerkki 3.
Asiassa on 500 grammaa 25-prosenttista suolahappoa. Lasketaan, paljonko astiaan on lisättävä vettä, jotta saataisiin 15-prosenttista suolahappoa.
Merkitään lisättävän veden määrää x:llä, tällöin saadaan yhtälö
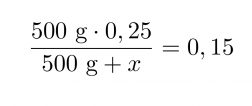
Klikkaa kuva suuremmaksi!
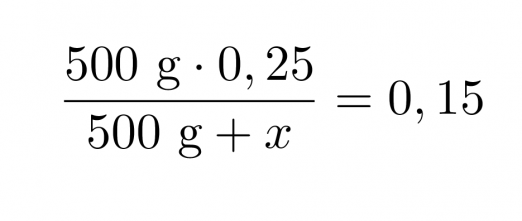
Klikkaa kuva suuremmaksi!
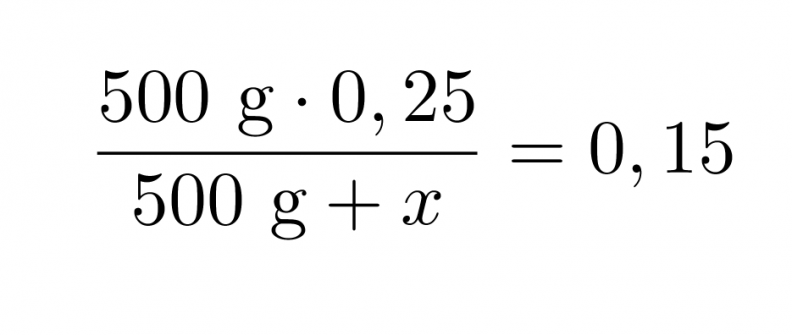
Klikkaa kuva suuremmaksi!
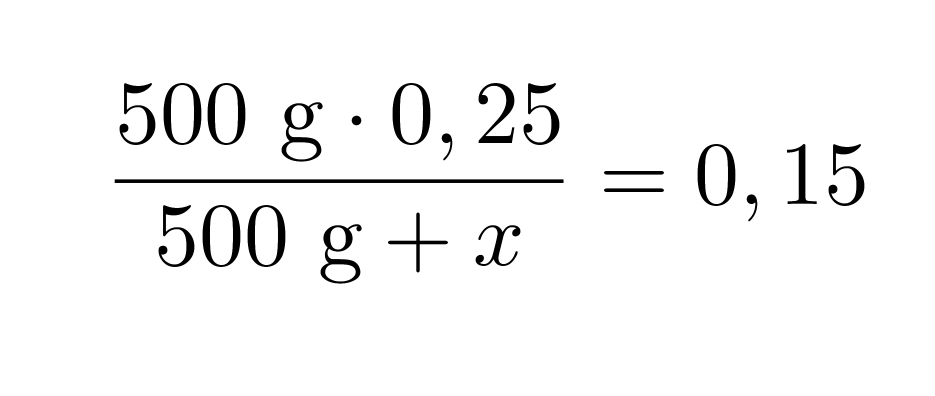
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaistaan yhtälö normaaleja yhtälön ratkaisutapoja soveltaen.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Astiaan on lisättävä 330 g vettä.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014