16. Prosenttilausekkeet
Tutkittaessa miten jokin prosentuaalinen muutos vaikuttaa yleisesti, ei voida valita muutosten kohteeksi yksittäistä lukuarvoa. Tällöin muutokset on kohdistettava muuttujaan, jonka paikalle voidaan halutessa sijoittaa mikä tahansa lukuarvo. Prosenttilaskuissa vakiintunut käytäntö on merkitä muuttujia aakkosten alkupään kirjaimilla a, b, ….
Jos laskut sisältävät esimerkiksi kaksi eri muuttujaa, on pyrittävä löytämään jokin yhteys eri muuttujien välille. Näin päästään eroon toisesta muuttujasta.
Esimerkki 1.
Kirjoita tuotteen uusi hinta lausekkeena, kun vanhaa hintaa a
- korotetaan 32 %
- alennetaan 12 %.
Ratkaisu:
a) Hinta kasvaa 132 %:iin eli tulee 1,32-kertaiseksi. Uusi hinta on 1,32a.
b) Hinta alenee 88 %:iin eli tulee 0,88-kertaiseksi. Uusi hinta on 0,88a.
Esimerkki 2.
Lukuun lisätään ensin 15 % ja sitten siitä vähennetään 35 %. Montako prosenttia saatu luku on alkuperäisestä luvusta?
Ratkaisu:
Ensimmäinen muutos:
100 % + 15 % = 115 % eli saadaan prosenttikerroin 1,15.
Toinen muutos:
100 % – 35 % = 65 % eli saadaan prosenttikerroin 0,65.
Koska lukua ei ole annettu, merkitään sitä muuttujalla a.
Muutetaan lukua vaadittujen prosenttien verran:

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Lasketaan lopuksi, montako prosenttia tämä on alkuperäisestä luvusta.
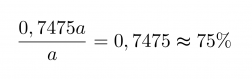
Klikkaa kuva suuremmaksi!
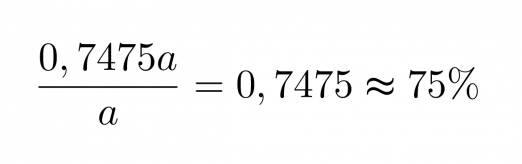
Klikkaa kuva suuremmaksi!
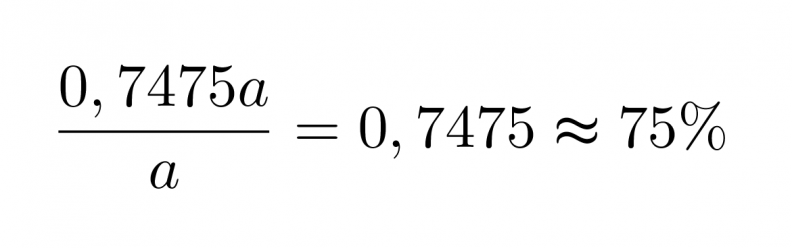
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
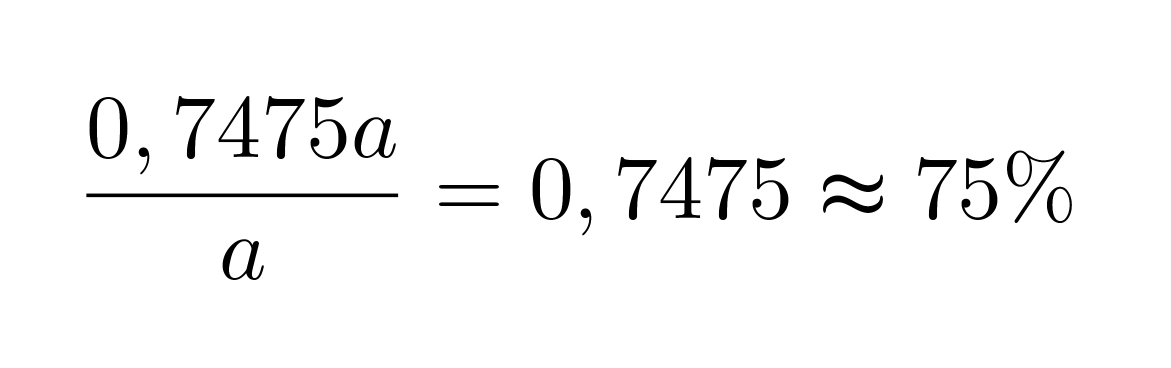
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Luku on 75 % alkuperäisestä luvusta.
Esimerkki 3.
Aurinkokuivatuksella haihdutetaan tomaatista vettä. Tuoreen tomaatin vesipitoisuus on 80 % ja aurinkokuivatetun tomaatin 25 %. Montako prosenttia vedestä on haihdutettava?
Ratkaisu:
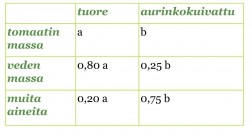
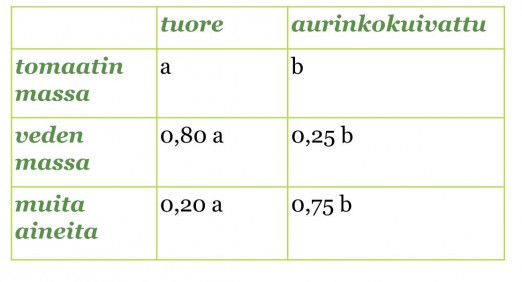
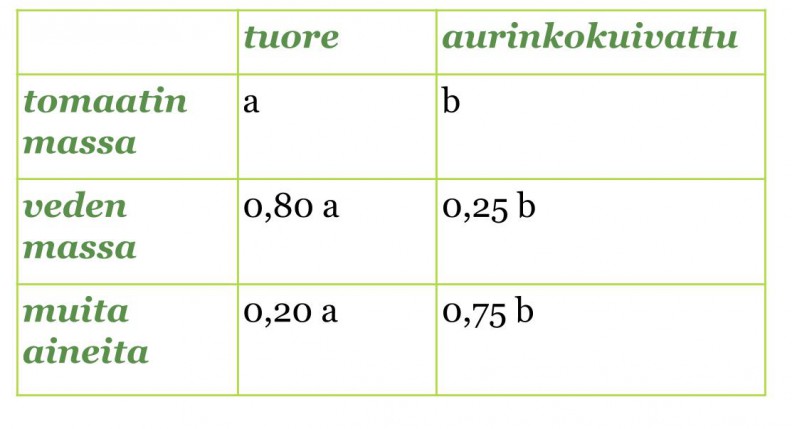
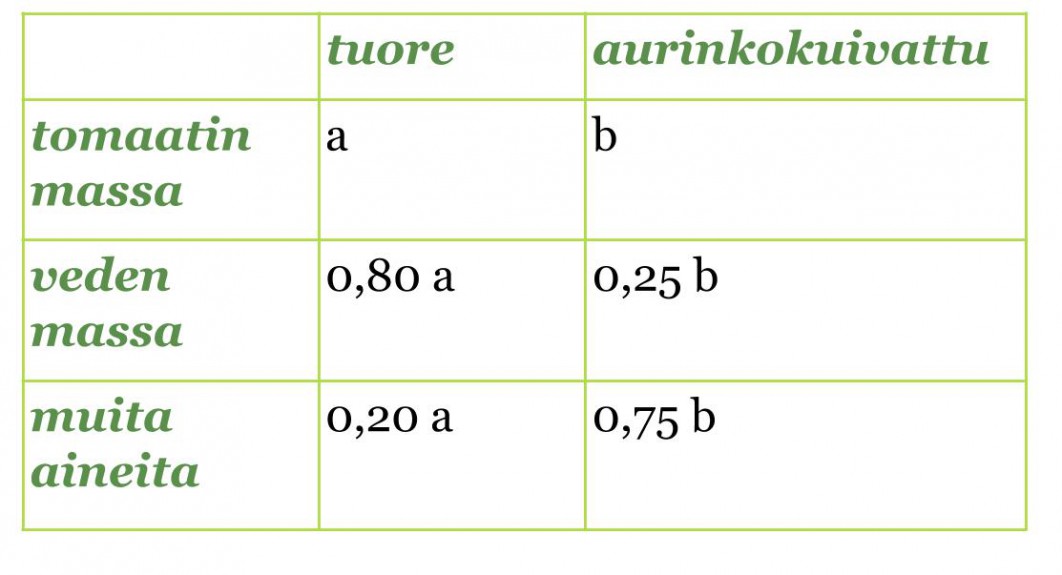
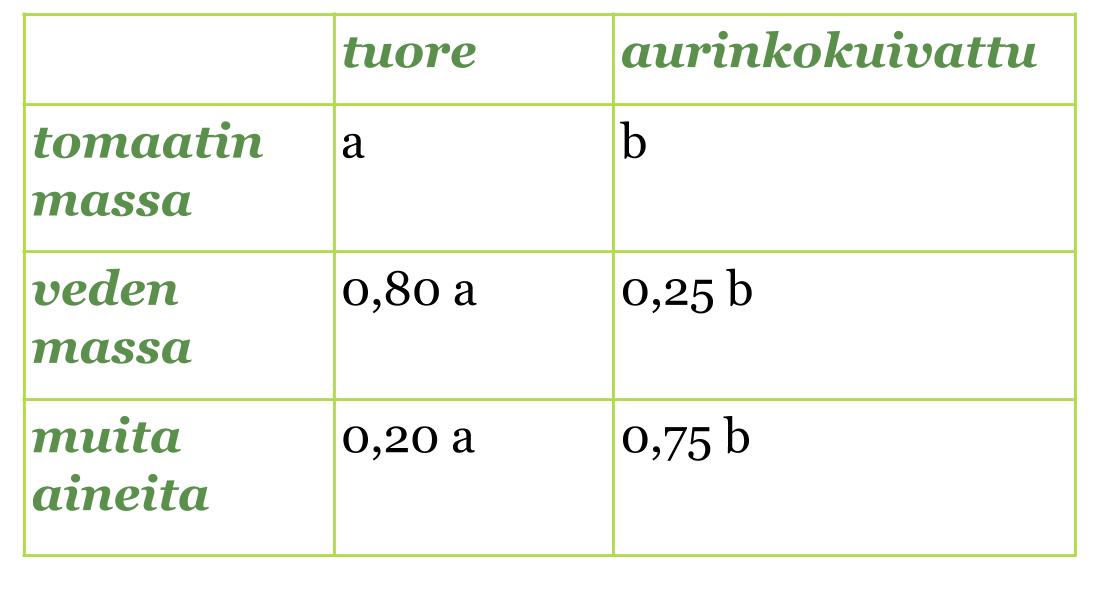
Merkitään tuoreen tomaatin massaa a:lla ja kuivatetun tomaatin massaa b:llä. Lasketaan muiden aineiden määrät vähentämällä 100 %:sta veden osuus ja taulukoidaan molempien tomaattien veden ja muiden aineiden osuudet.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Haihdutuksessa ainoastaan veden määrä vähenee. Muiden aineiden määrä pysyy samana. Tämän tiedon perusteella voimme muodostaa muita aineita koskevan yhtälön ja ratkaista sen a:n suhteen.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jäljellä olevan veden osuus alkuperäisestä vedestä on

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vettä on siis haihtunut 1 − 0,08333… = 0,9166… ≈ 92%
Vastaus: Tomaatin vedestä on haihdutettava 92 %.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014
Monta peräkkäistä prosentuaalista muutosta