17. Binomin neliö ja neliöiden erotus*
Jos jokin binomi eli polynomi, jossa on kaksi termiä, korotetaan toiseen potenssiin, muodostuu binomin neliö. Binomin neliö voidaan ratkaista polynomien kertolaskun avulla eli kertomalla kantaluku itsellään.
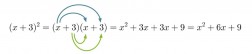
Klikkaa kuva suuremmaksi!
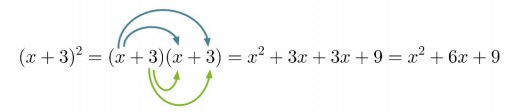
Klikkaa kuva suuremmaksi!
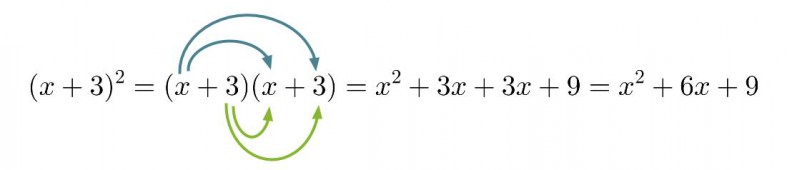
Klikkaa kuva suuremmaksi!
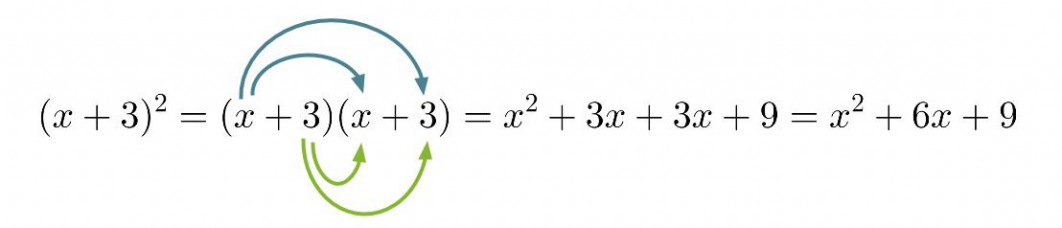
Klikkaa kuva suuremmaksi!
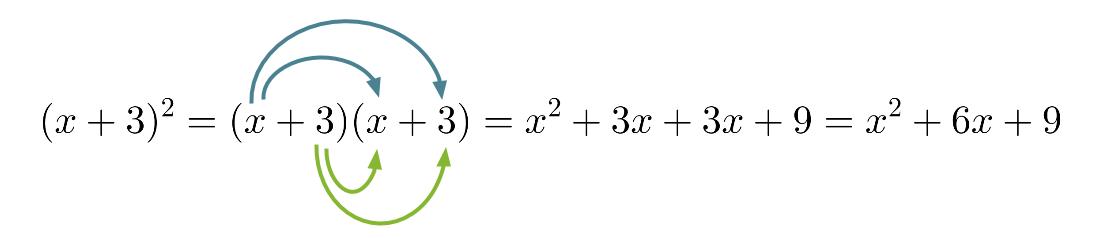
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Helpommalla kuitenkin päästään käyttämällä binomin neliöiden laskukaavaa.

Klikkaa kuva suuremmaksi!
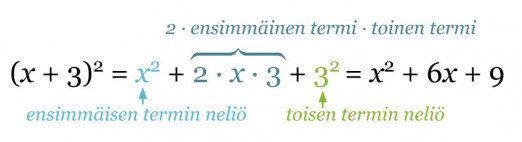
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
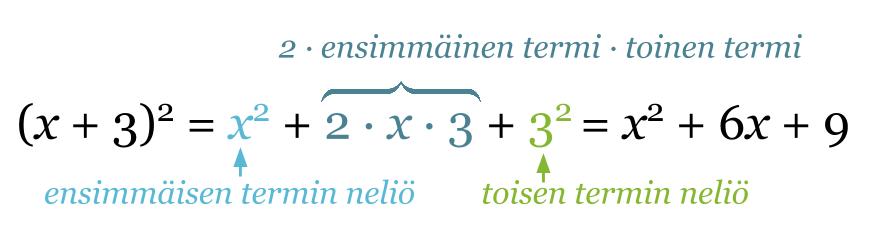
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Binomien neliöiden laskukaavat ovat
(a + b)² = a² + 2ab + b² ja
(a – b)² = a² – 2ab + b²
Sovelletaan polynomien kertolaskua tilanteeseen, jossa kahden termin summa kerrotaan vastaavien termien erotuksella. Tulos voidaan päätellä myös käyttämällä neliöiden erotuksen laskukaavaa.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kahden neliön erotus on yhtä suuri kuin termien neliöjuurien summa kerrottuna niiden erotuksella.
a2 – b2 = (a + b)(a – b)
Huom! Vastaavaa kaavaa neliöiden summalle ei ole.
Esimerkki 1.
Kirjoitetaan binomien neliöt auki käyttäen laskukaavoja.
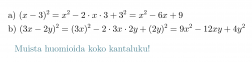
Klikkaa kuva suuremmaksi!
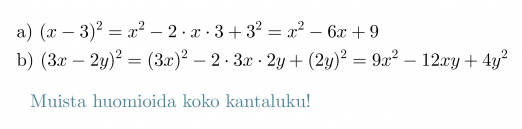
Klikkaa kuva suuremmaksi!
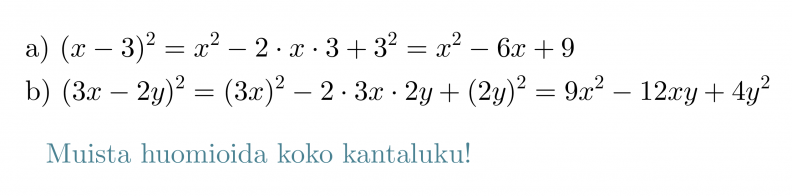
Klikkaa kuva suuremmaksi!
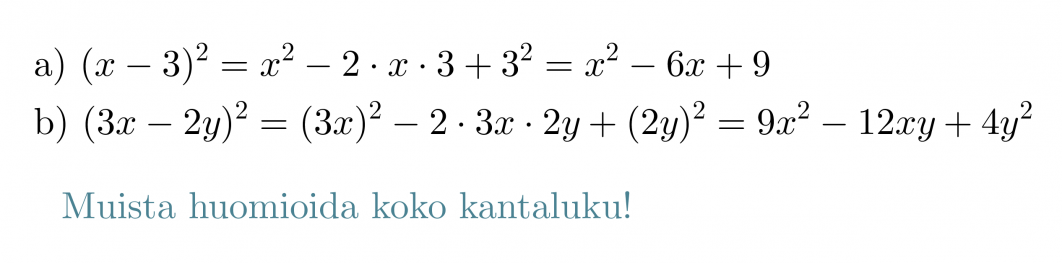
Klikkaa kuva suuremmaksi!
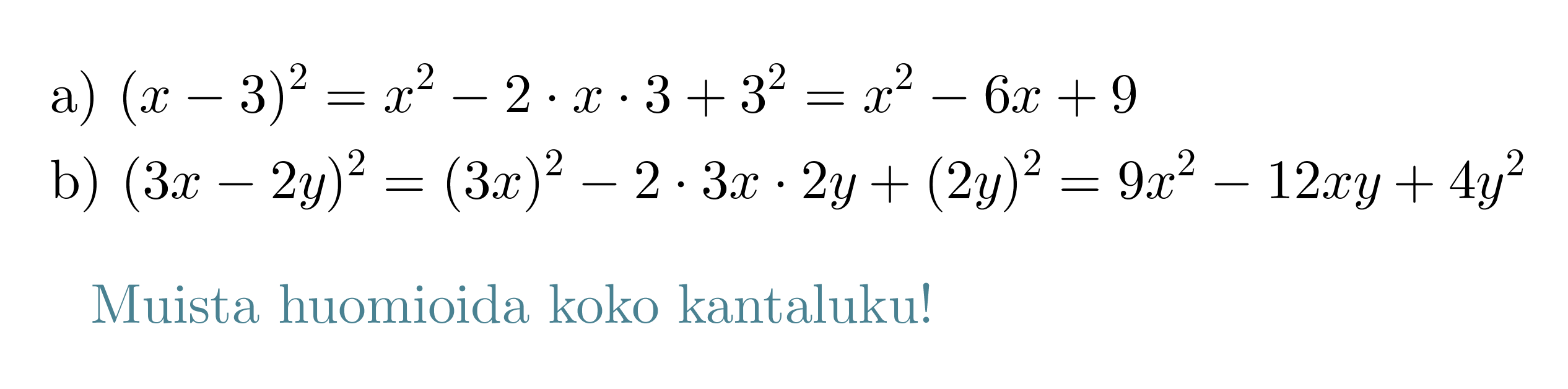
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Jaetaan binomit tekijöihin tarkastelemalla ensiksi minkä termien neliöt ovat kyseessä.
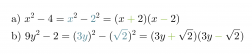
Klikkaa kuva suuremmaksi!
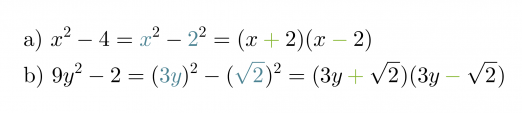
Klikkaa kuva suuremmaksi!
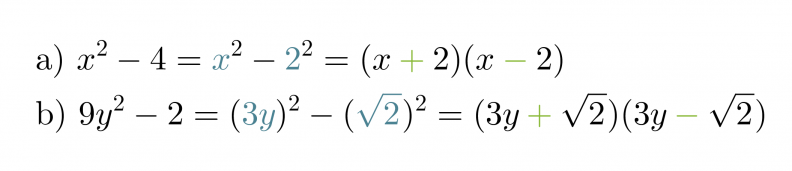
Klikkaa kuva suuremmaksi!
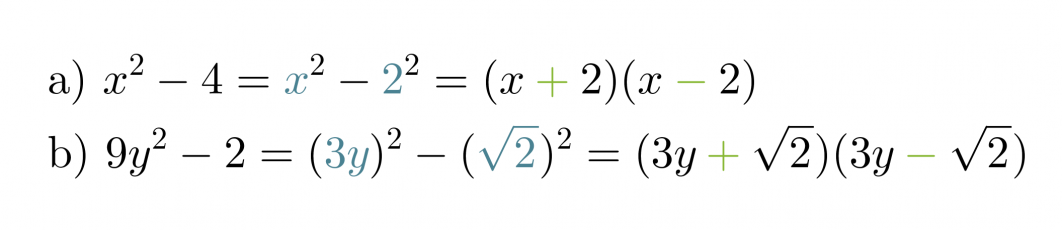
Klikkaa kuva suuremmaksi!
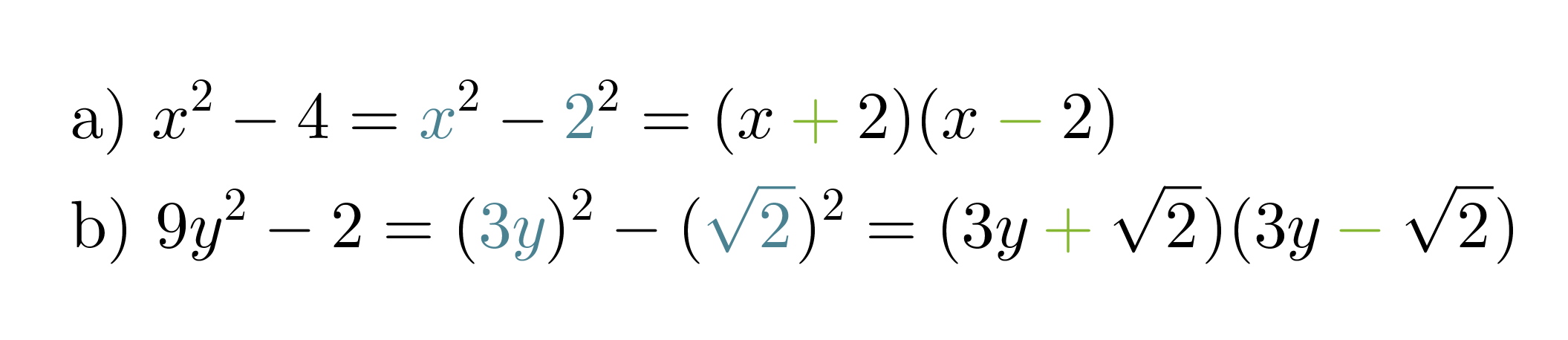
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Binomin neliön laskukaavaa voidaan soveltaa myös toisinpäin eli toisen asteen polynomien termien perusteella voidaan päätellä, saadaanko se jonkin binomin neliöstä.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
Onko polynomi 9x2 + 6x + 1 jonkin binomin neliö?
Ratkaisu:
Polynomin ensimmäinen ja viimeinen termi ovat positiivisia. Ensimmäinen termi on 3x:n neliö ja viimeinen luvun 1 neliö.
Tutkitaan mikä olisi keskimmäisen termin oltava, jotta kyseessä olisi binomin neliö.
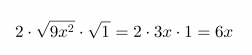
Klikkaa kuva suuremmaksi!
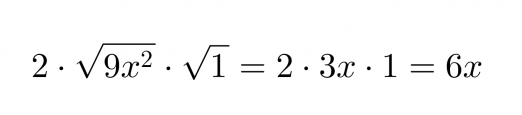
Klikkaa kuva suuremmaksi!
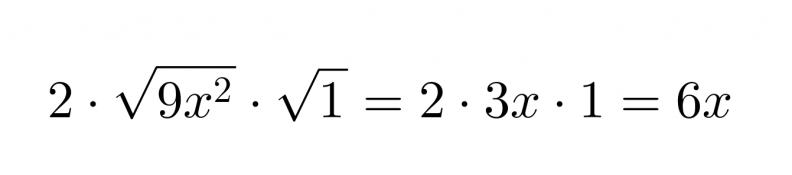
Klikkaa kuva suuremmaksi!
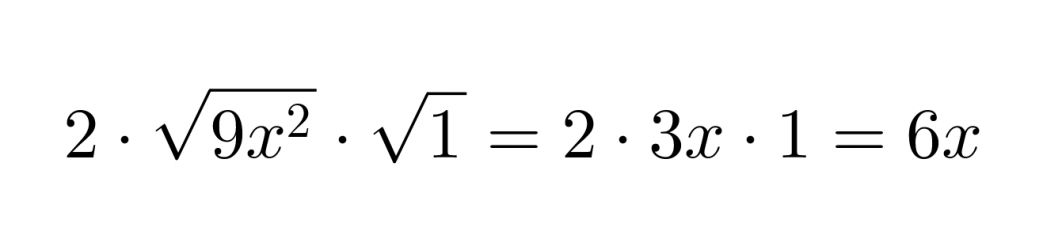
Klikkaa kuva suuremmaksi!
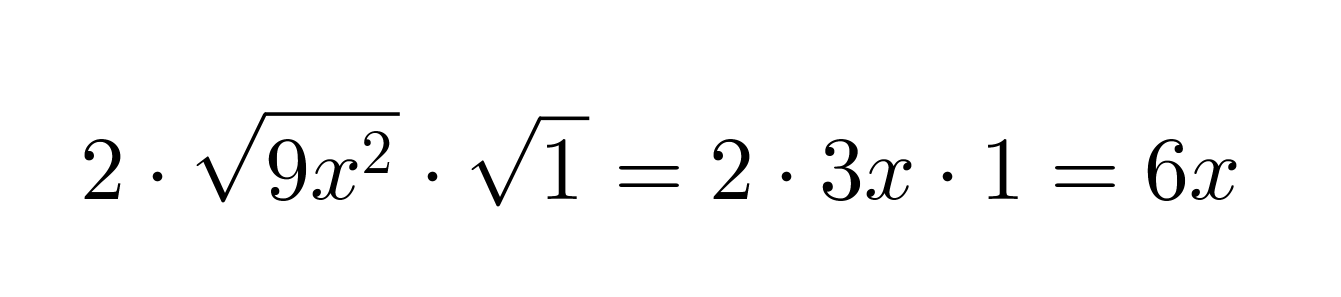
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Se, onko binomissa kyseessä vähennys- vai yhteenlasku, selviää keskimmäisen termin etumerkistä.
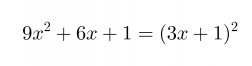
Klikkaa kuva suuremmaksi!
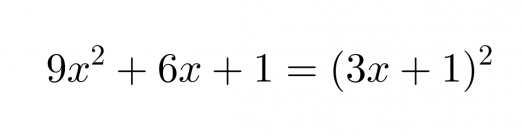
Klikkaa kuva suuremmaksi!
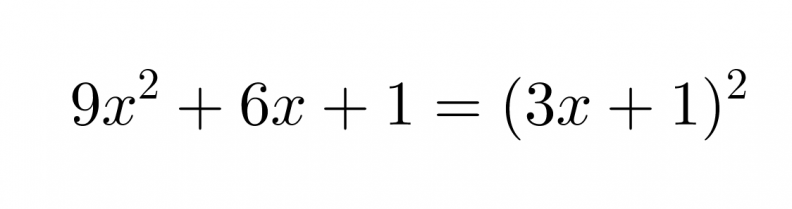
Klikkaa kuva suuremmaksi!
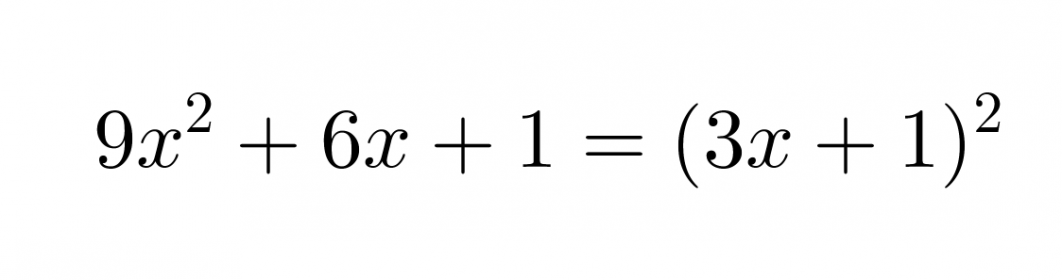
Klikkaa kuva suuremmaksi!
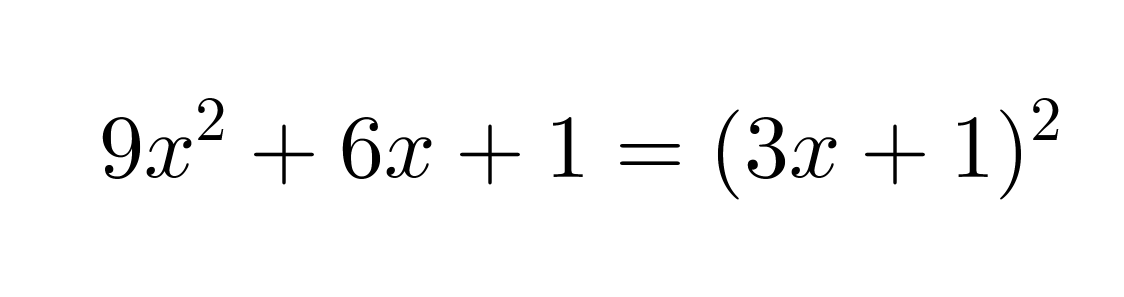
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Polynomi 9x2 + 6x + 1 on binomin 3x + 1 neliö.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014
Polynomi on jonkin binomin neliö, jos