18. Vektorin käsite*
Vektoreilla eli nuolilla kuvataan suureita, joihin liittyy suuruuden lisäksi myös suunta.Nuolen pituus kuvaa suureen suuruutta ja nuolen kärki osoittaa suunnan. Vektorisuureita ovat esimerkiksi nopeus ja voima. Jos auto ajaa tietyllä nopeudella, voidaan aina ilmoittaa mihin suuntaan se on ajamassa. Nopeutta ei voi olla olemassa ilman suuntaa. Skalaarisuureilla puolestaan on ainoastaan suuruus ja ne ilmoitetaan mittaluvun sekä yksikön avulla. Skalaarisuureita ovat esimerkiksi massa, aika ja pinta-ala. Vektoreita käytetään erityisen paljon fysiikassa.
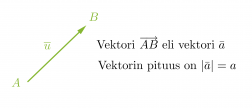
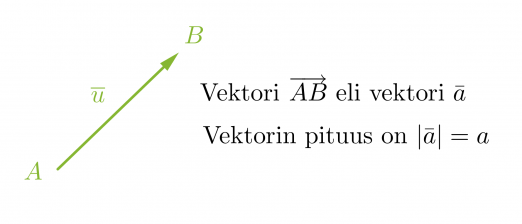
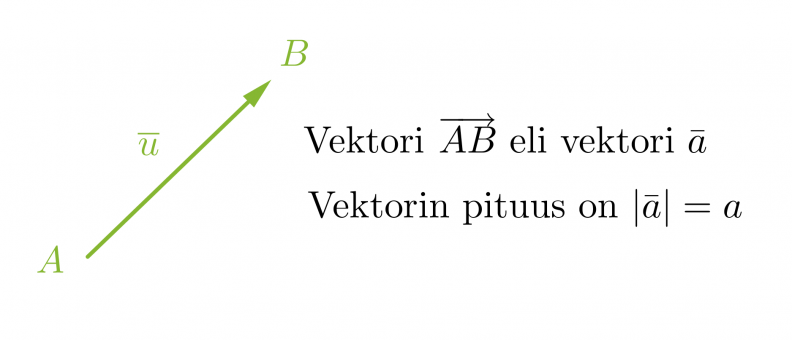
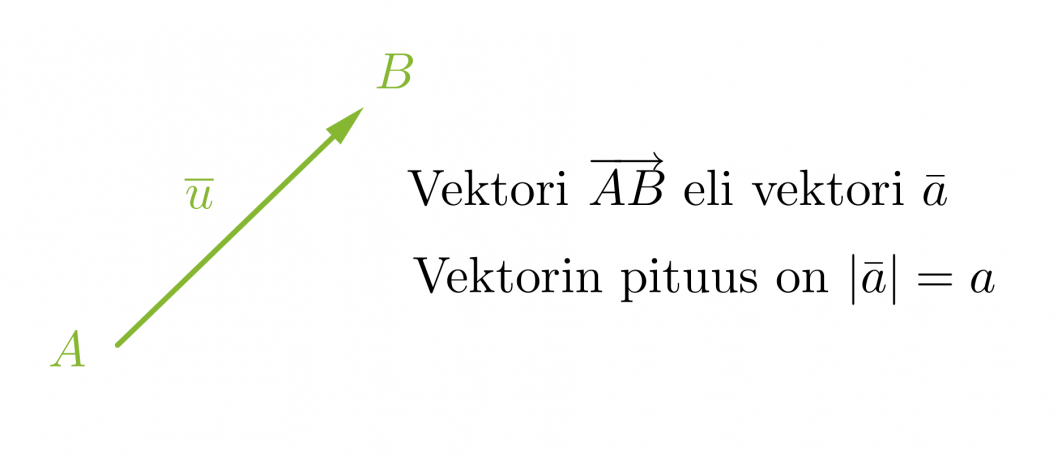
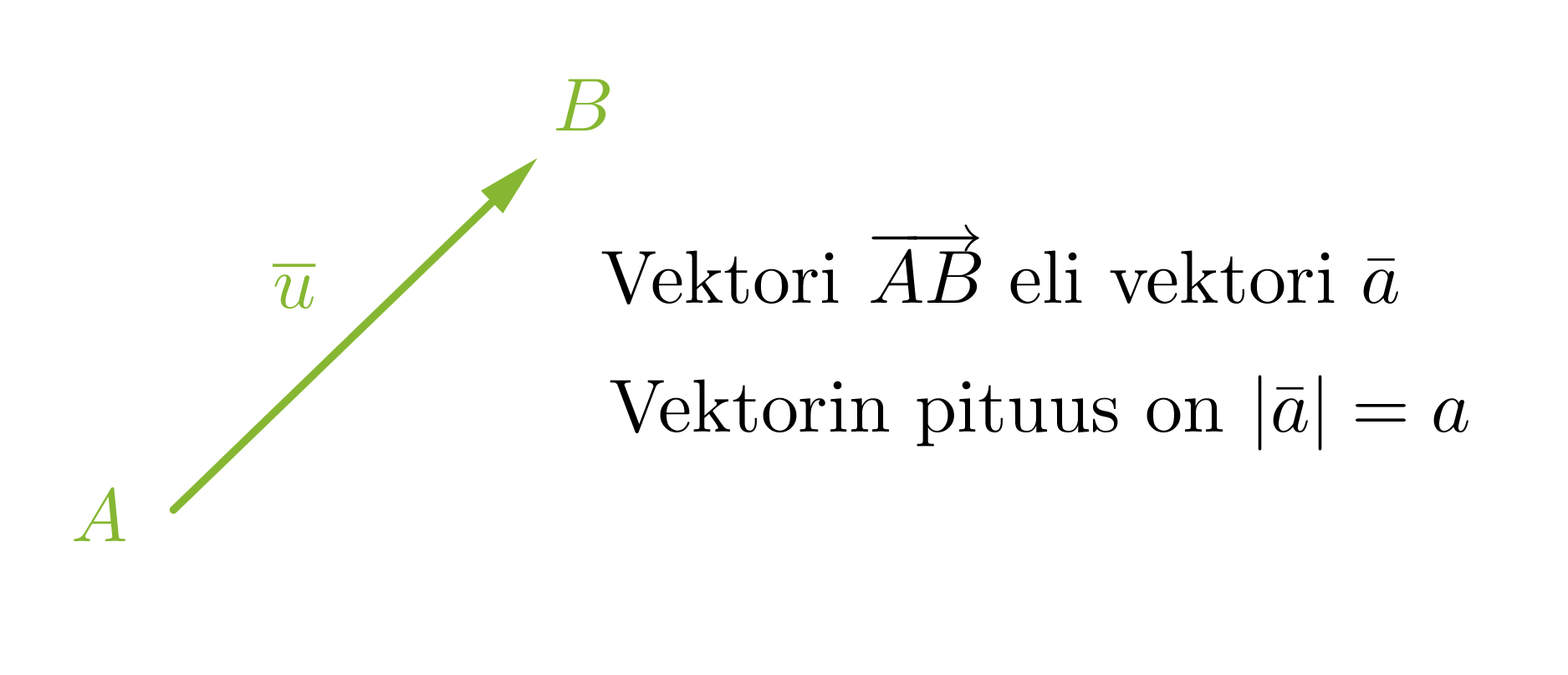
Jos kahta pistettä A ja B yhdistävälle janalle AB annetaan suunta eli sovitaan, että toinen pisteistä on janan alkupiste ja toinen sen loppupiste eli kärki, saadaan suuntajana. Vektoriksi kutsutaan mitä tahansa edellisen suuntajanan pituista ja suuntaista nuolta.
Vektorit voidaan nimetä kahdella eri tavalla: Jos vektorin nimeämiseen käytetään alku- ja loppupistettä, merkittään nämä isoilla kirjaimilla, joiden päällä on nuoli. Nuoli piirretään vasemmalta oikealle, jolloin loogisesti ensiksi mainitaan alkupiste ja seuraavaksi loppupiste. Vakiintunut käytäntö on myös nimetä vektorit pienellä kirjaimella, jonka päällä on joko nuoli tai pelkkä viiva. Vektorin pituus ilmaistaan joko laittamalla vektorisymboli itseisarvomerkkeihin tai jättämällä symbolista nuoli tai viiva pois.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
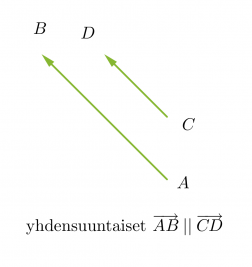
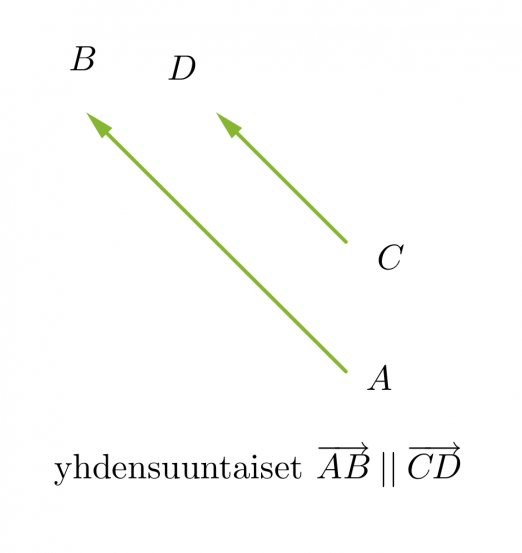
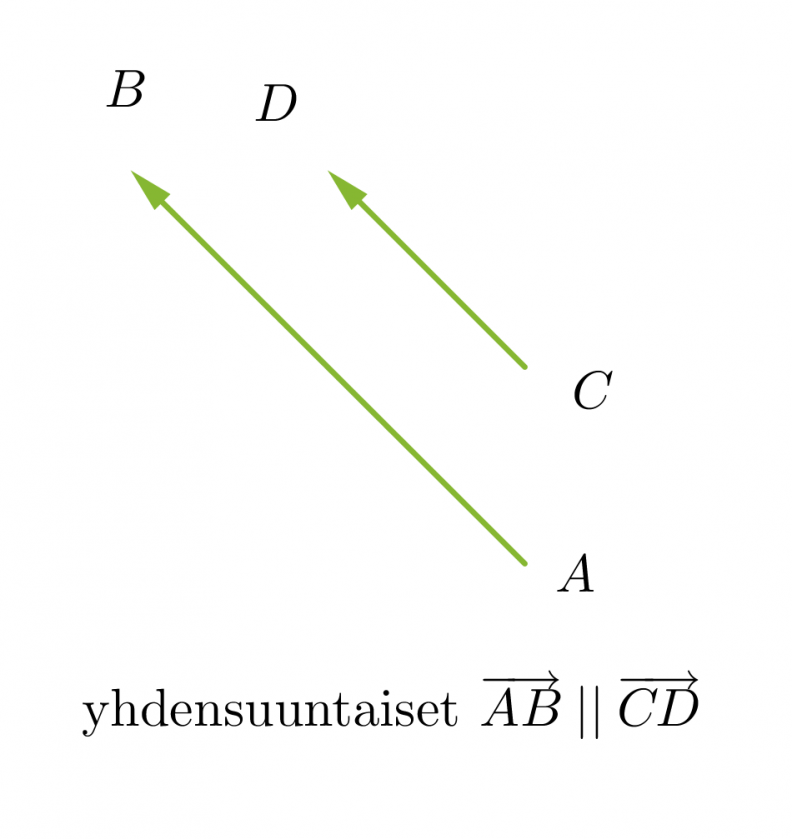
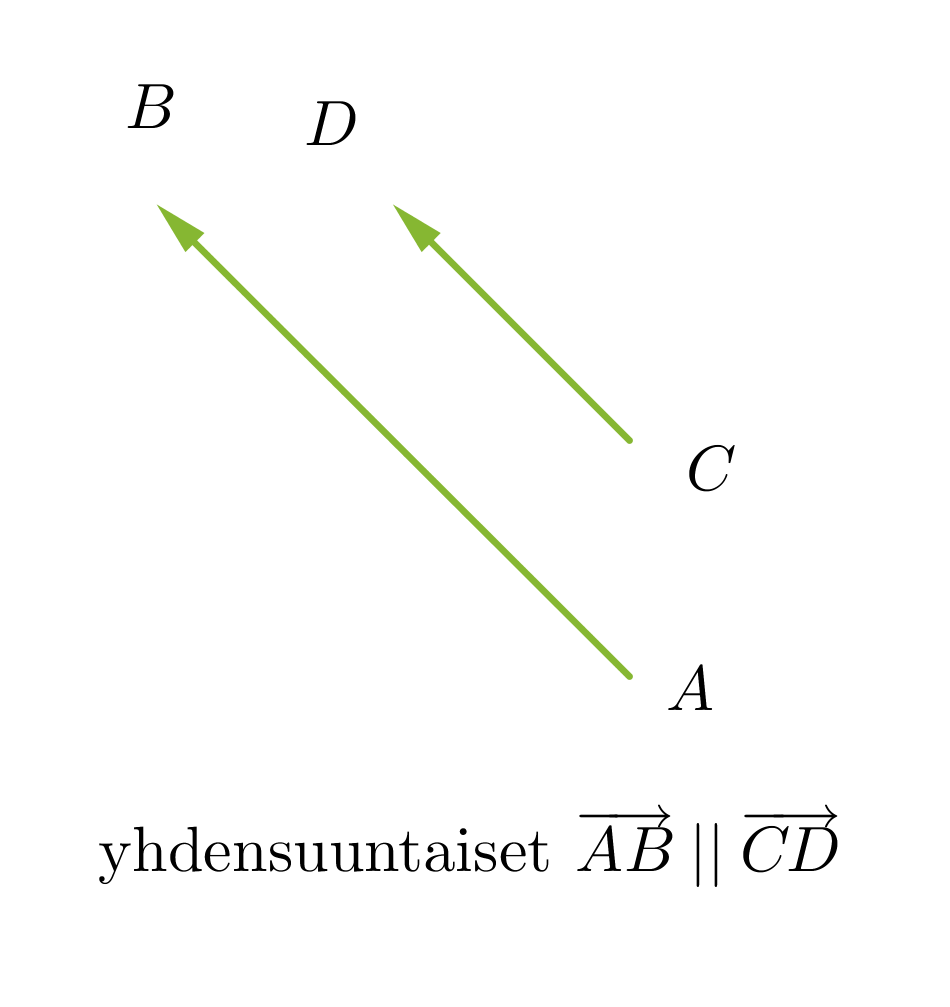
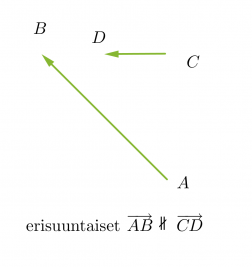
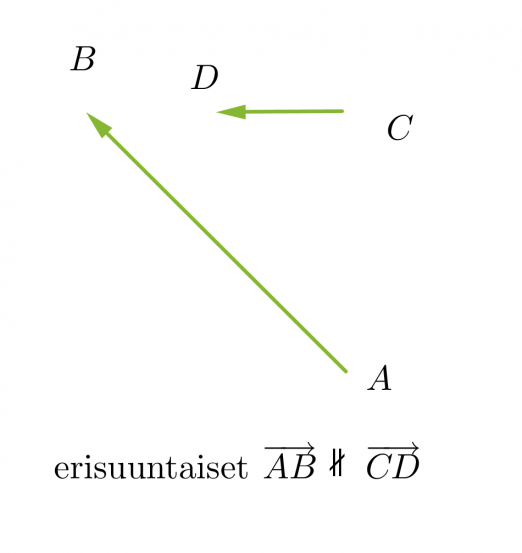
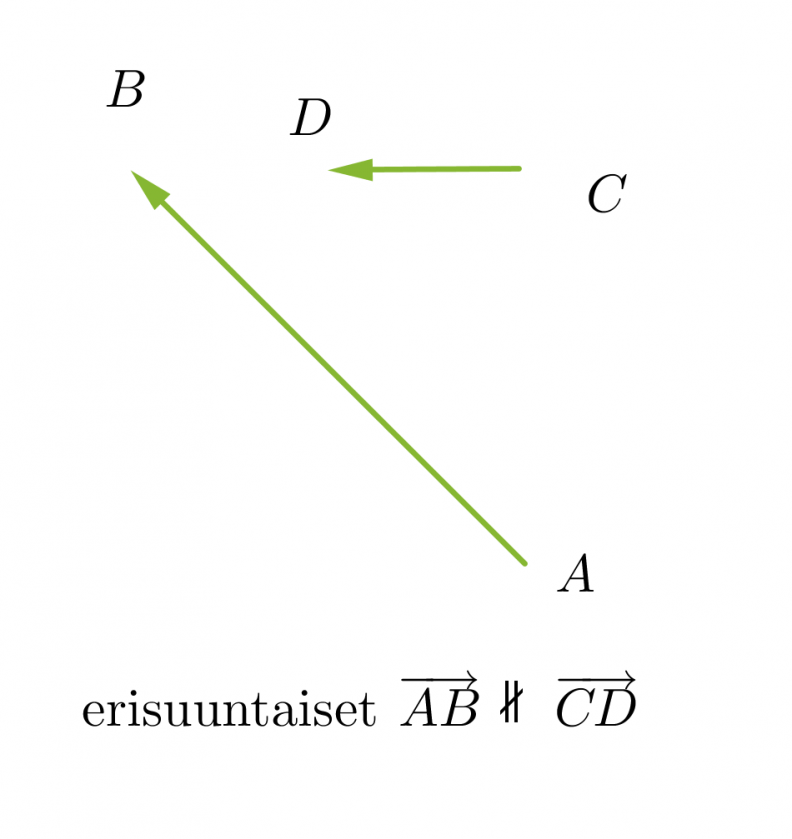
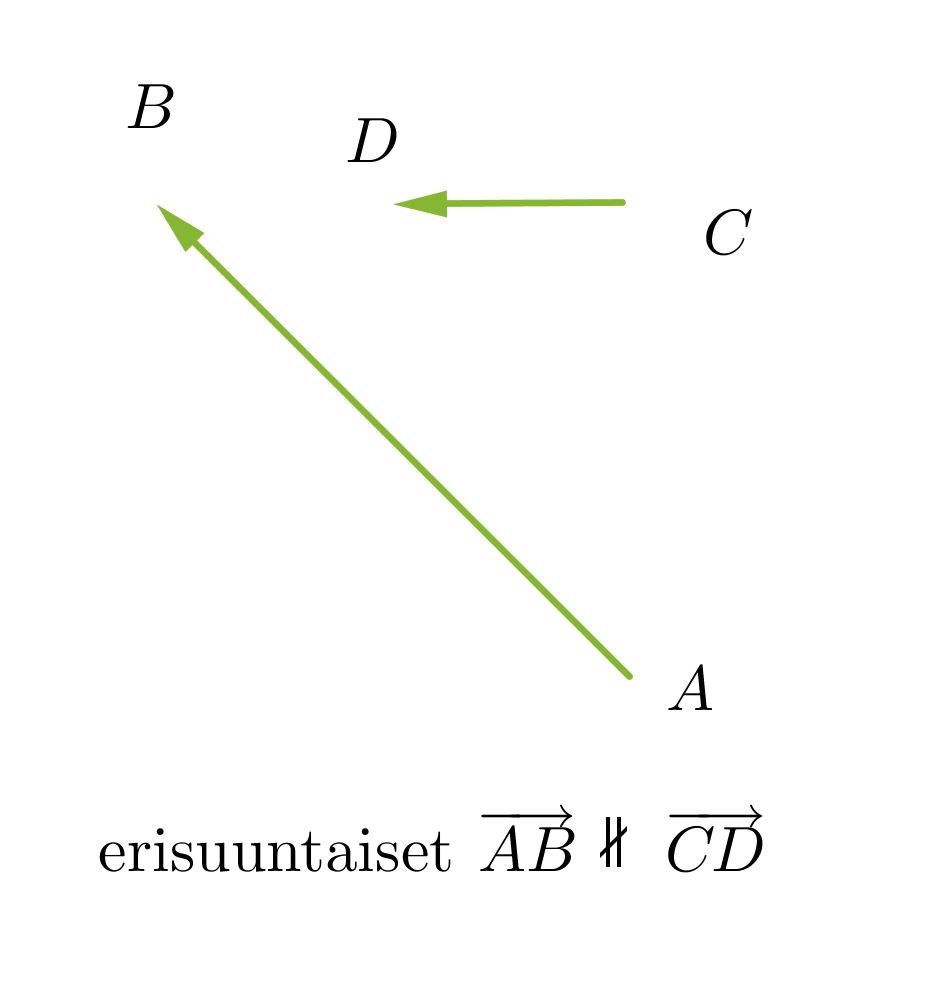
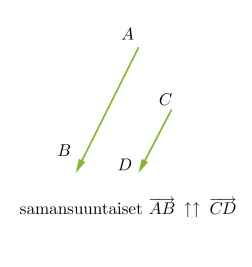
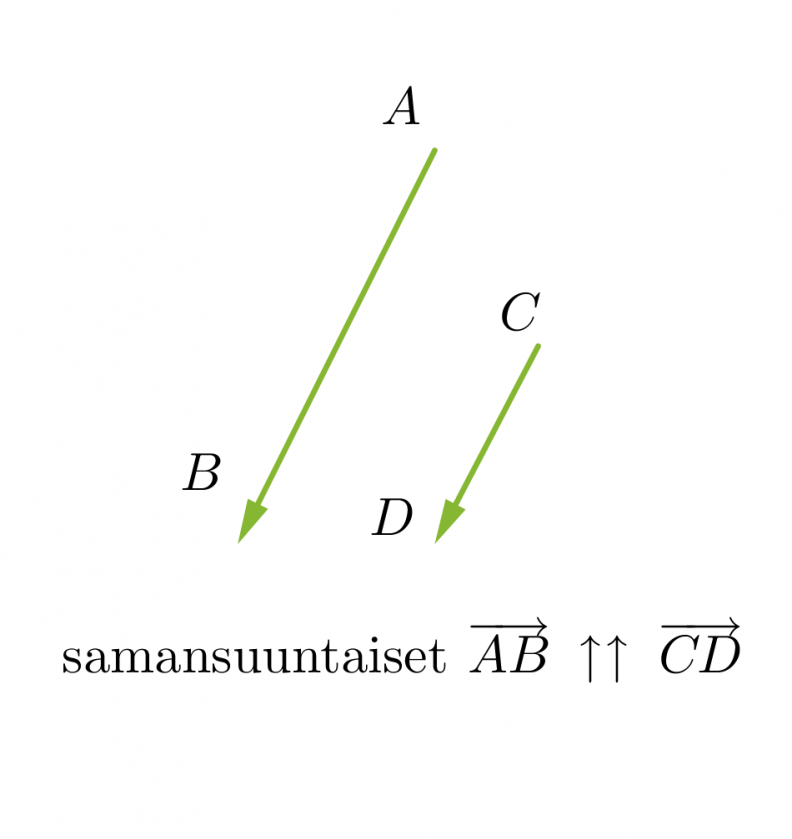
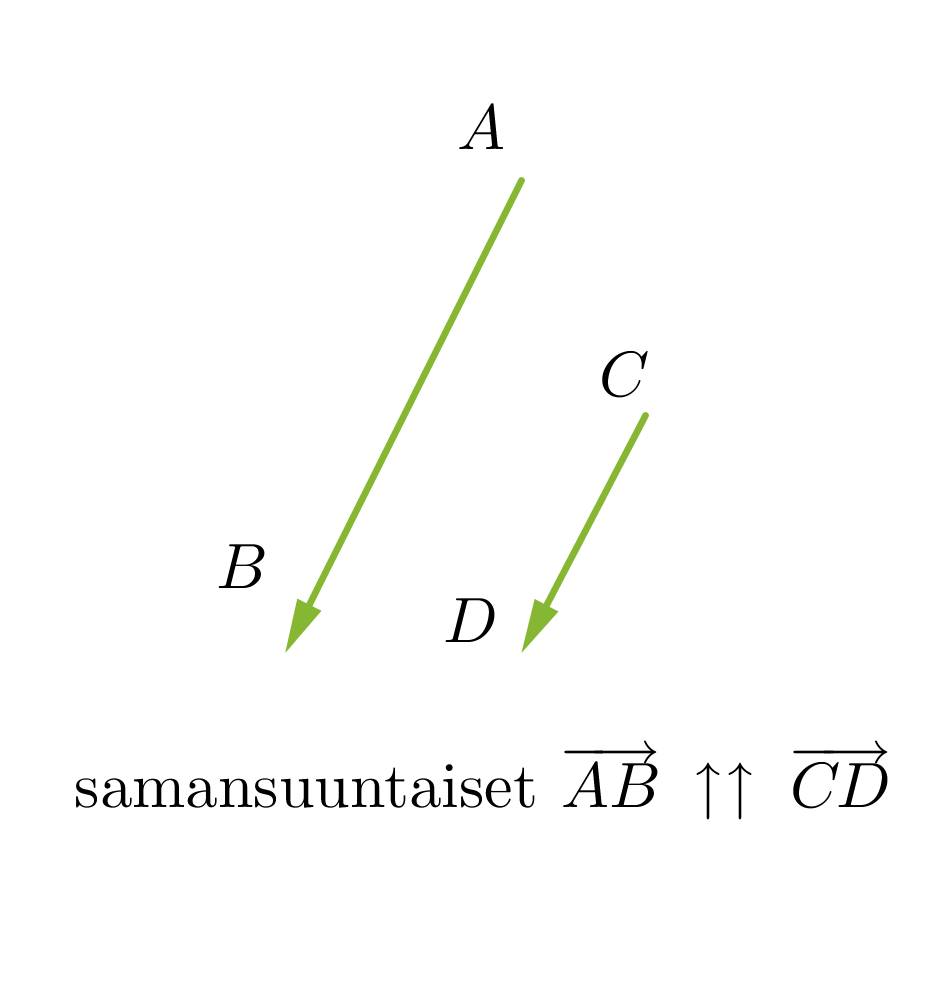
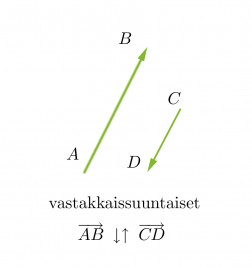
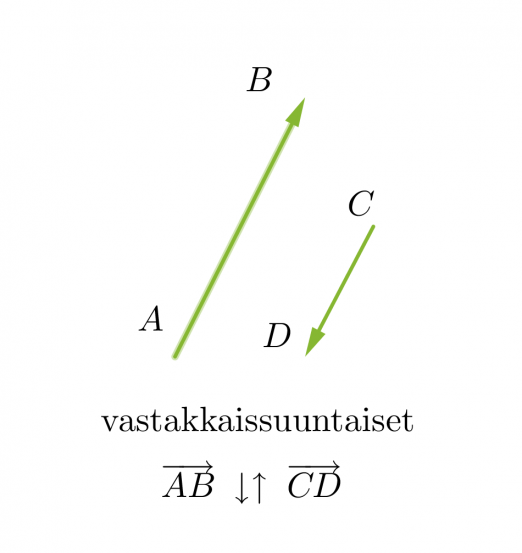
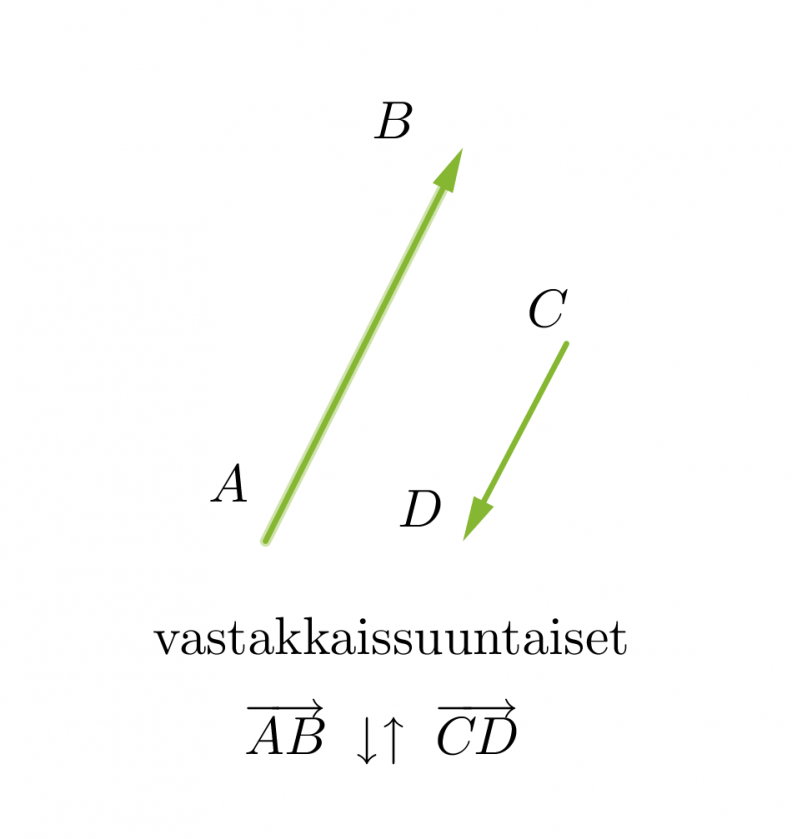
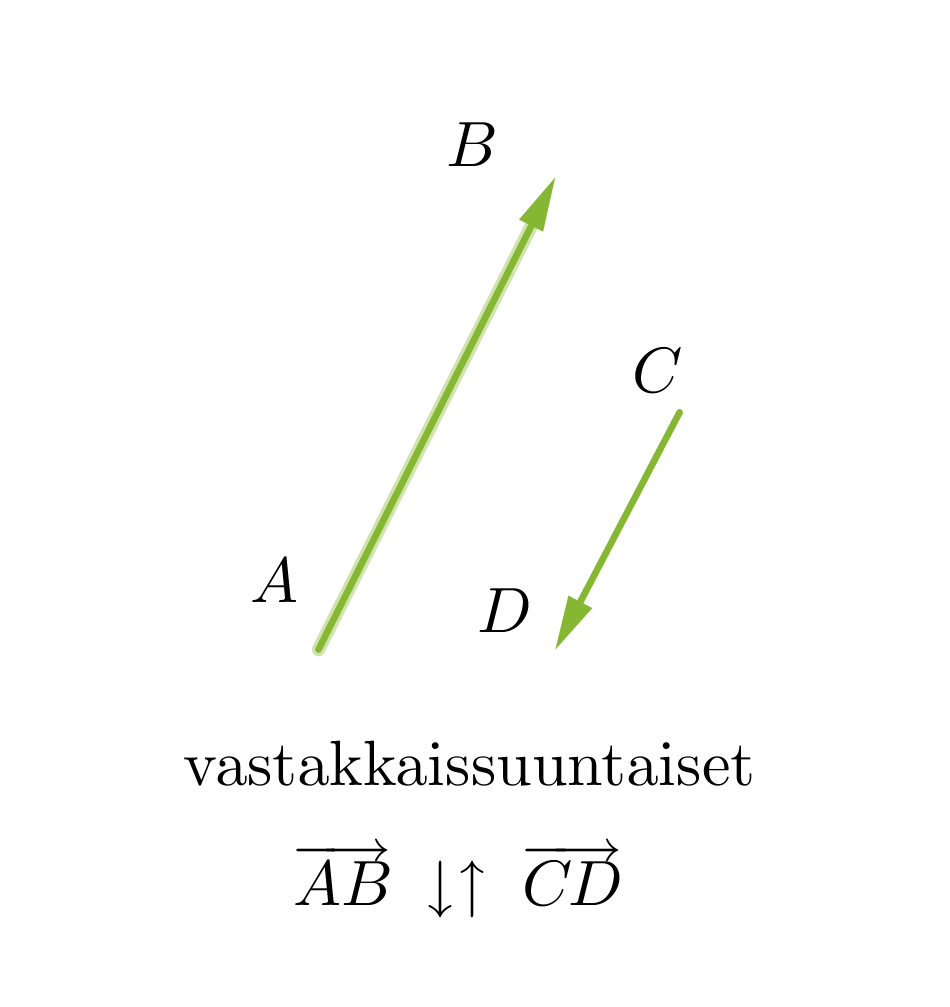
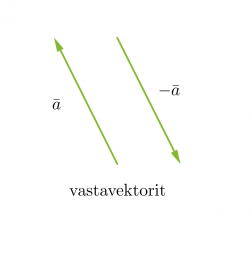
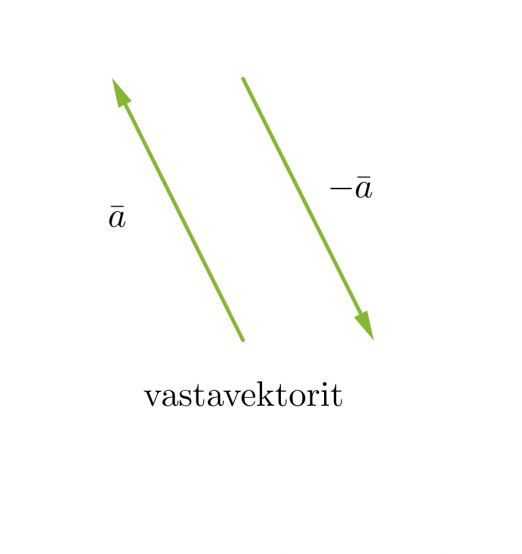
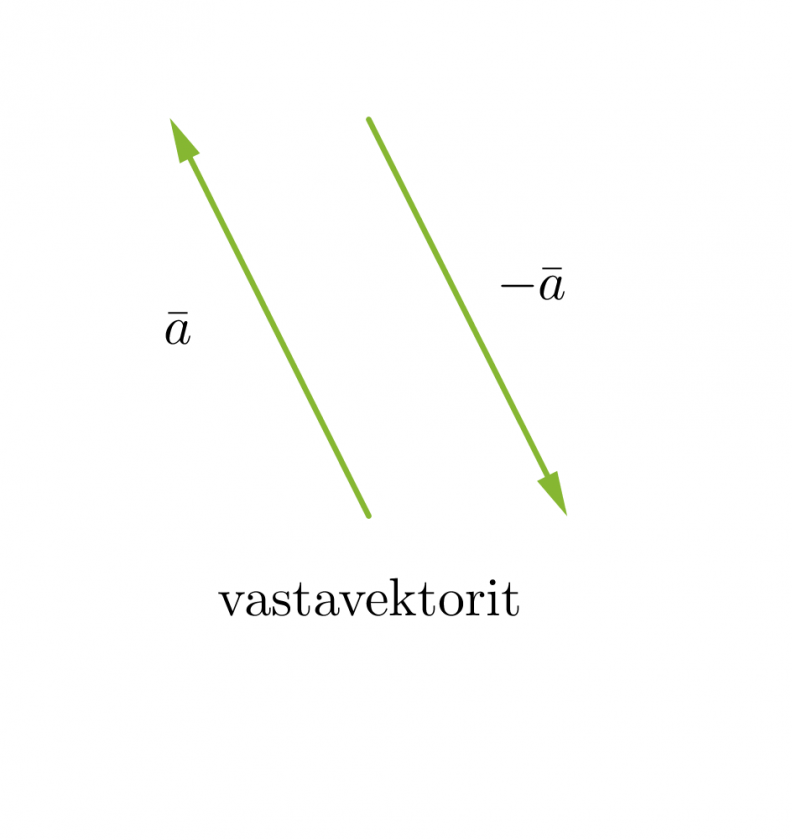
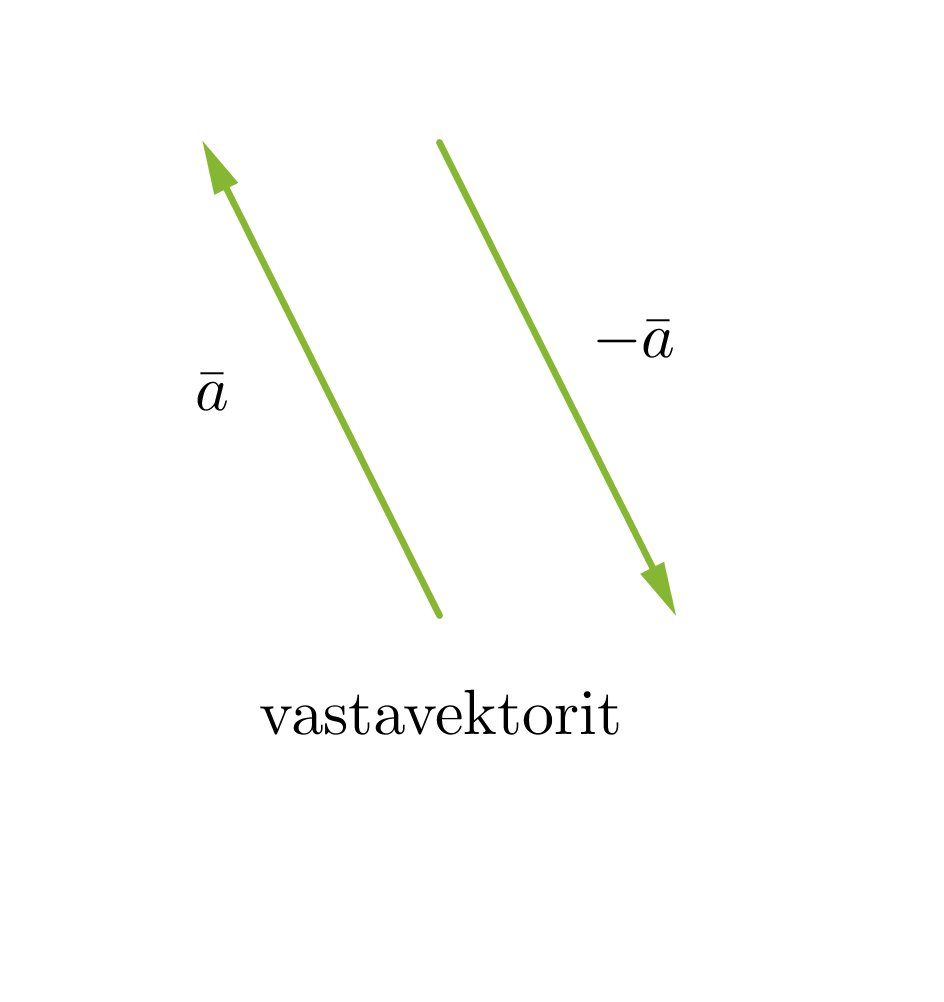
Vektorit voivat olla yhdensuuntaisia tai erisuuntaisia. Yhdensuuntaiset vektorit voivat lisäksi olla samansuuntaisia tai vastakkaissuuntaisia. Kaksi vektoria ovat samat, kun ne ovat yhtä pitkät ja samansuuntaiset. Vektorit, jotka ovat yhtä pitkät ja vastakkaissuuntaiset, ovat toistensa vastavektoreita. Jos vektorin alkupiste ja loppupiste yhtyvät, kutsutaan vektoria nollavektoriksi ja sitä merkitään . Nollavektorin pituus on nolla ja sen suunta on määrittelemätön.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
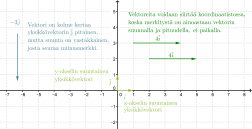
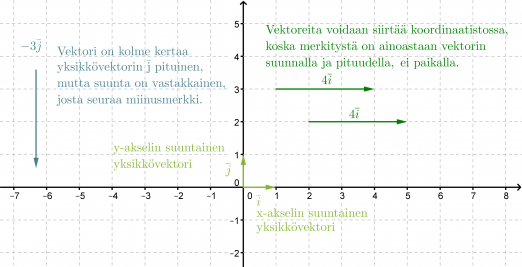
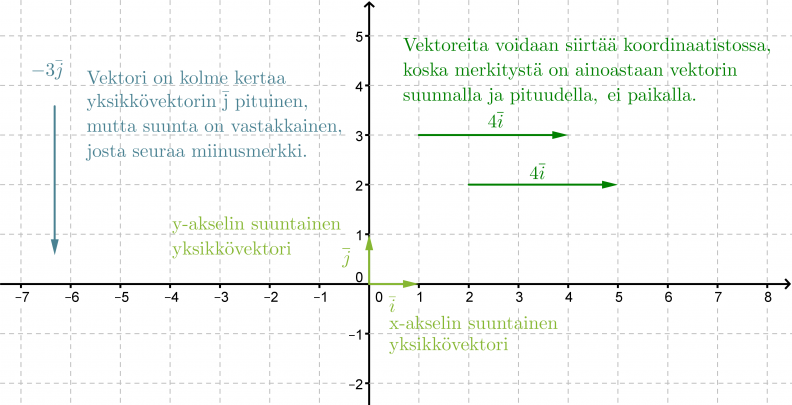
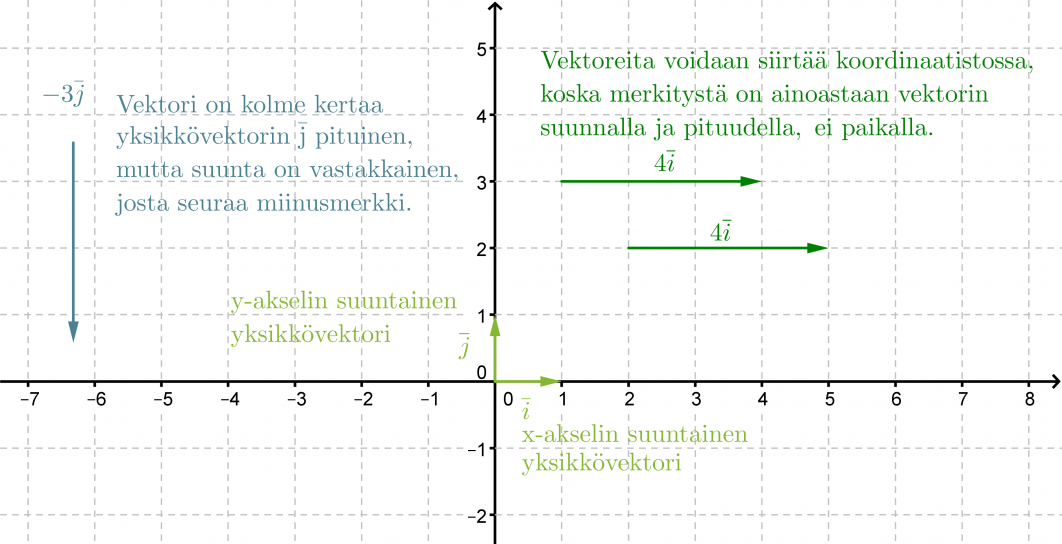
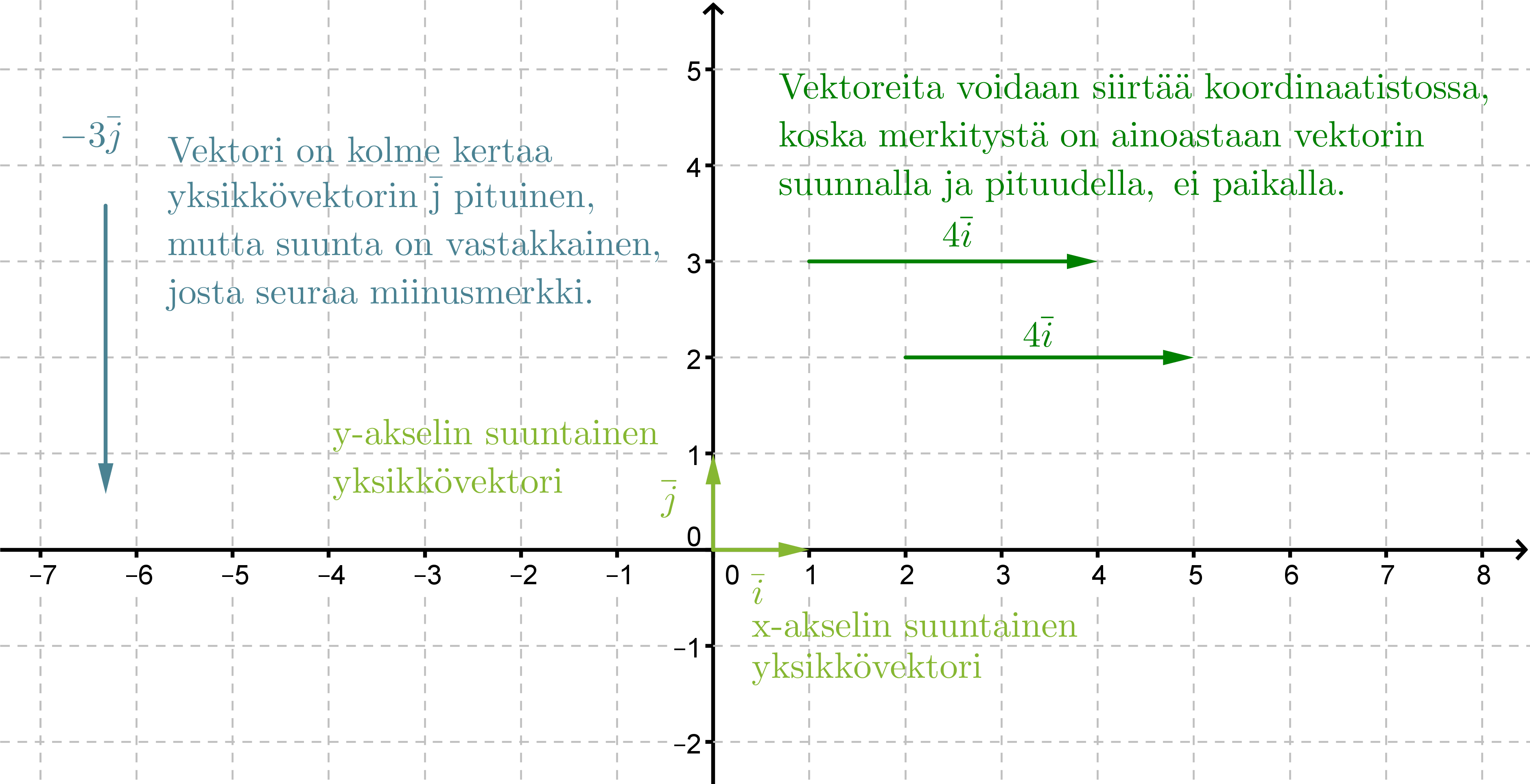
Vektoreita kuvataan yleensä koordinaatistossa. Samoin kun pituudessa tutkitaan, montako kertaa tietty mitta sisältyy tutkittavaan kohteeseen, on vektoriesityksenkin pohjauduttava johonkin mittaan. Koordinaatistossa vektoriesitys perustuu yksikkövektoreihin ja , joiden pituudet ovat 1. Yksikkövektori on x-akselin suuntainen ja y-akselin suuntainen. Molempien vektoreiden kärjet osoittavat akseleiden positiiviseen suuntaan.
Vektori voidaan kertoa reaaliluvulla, jolloin saadaan alkuperäisen vektorin kanssa yhdensuuntainen vektori. Jos vektori kerrotaan negatiivisella luvulla, muodostuu alkuperäisen vektorin kanssa vastakkaissuuntainen vektori eli vastavektori.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
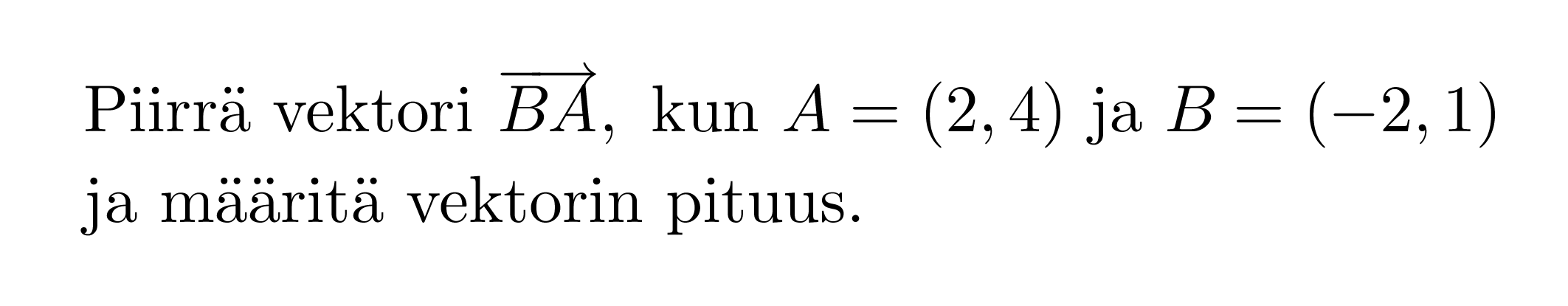
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
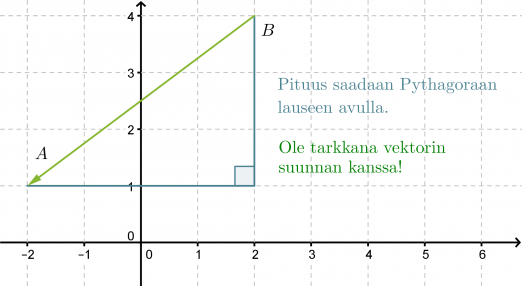
Ratkaisu:
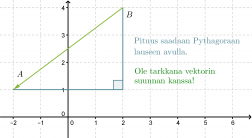
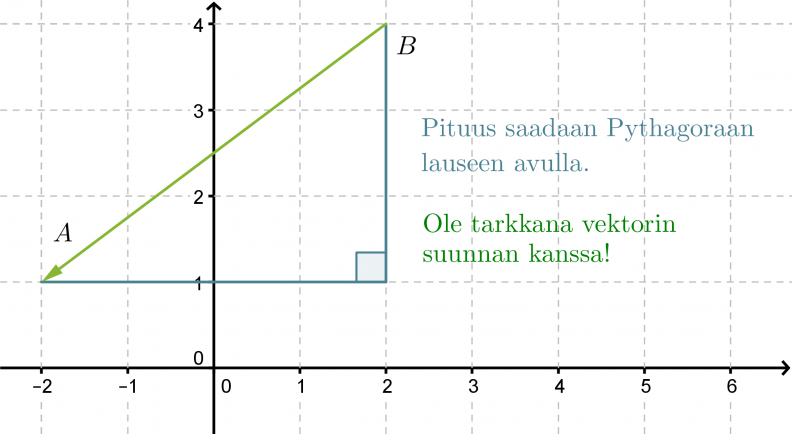
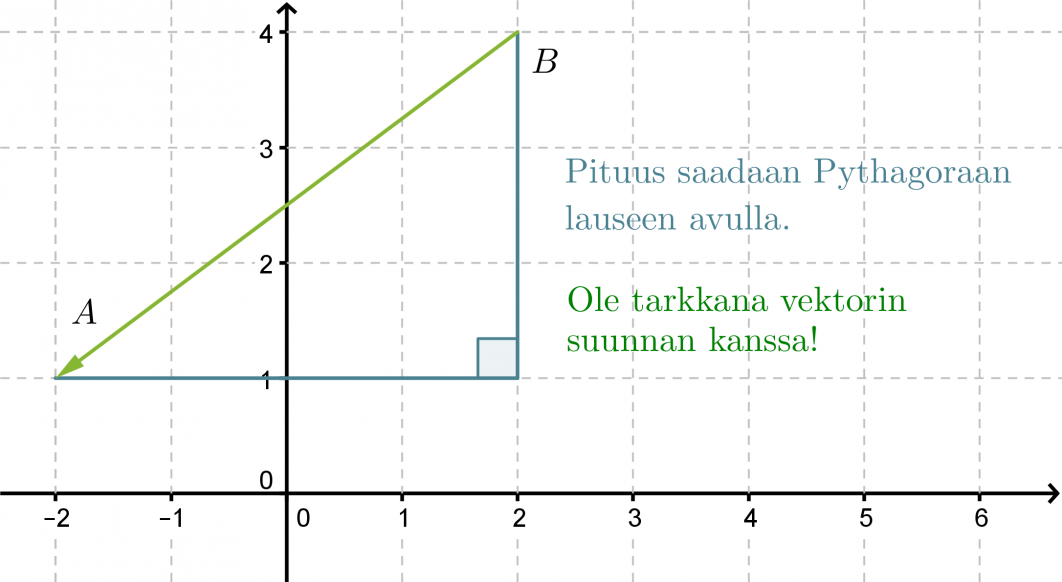
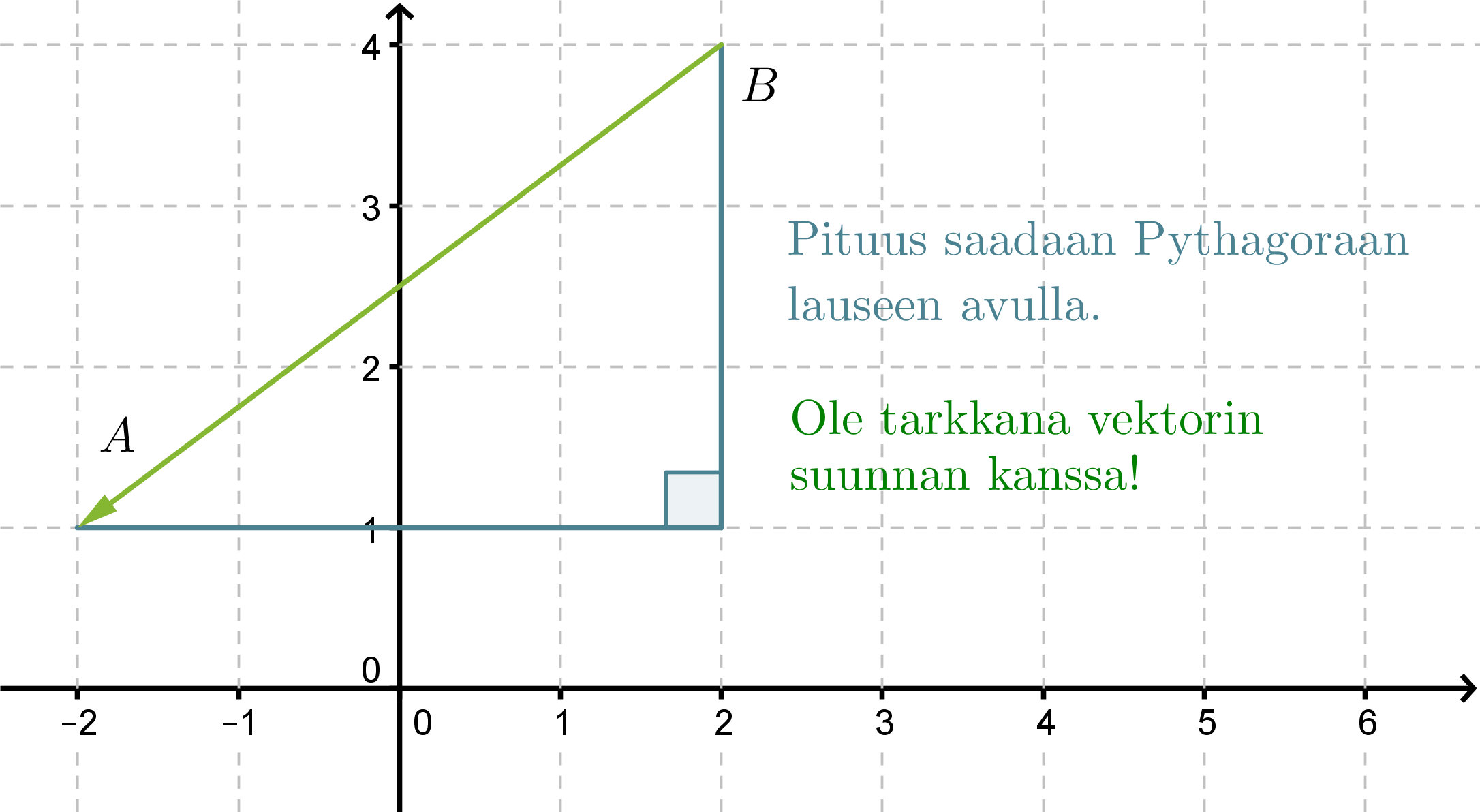
Sijoitetaan pisteet koordinaatistoon. Vektorin nimestä voidaan tulkita, että vektorin alkupiste on B ja loppupiste A.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
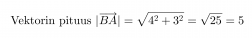
Klikkaa kuva suuremmaksi!
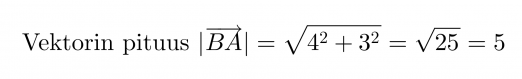
Klikkaa kuva suuremmaksi!
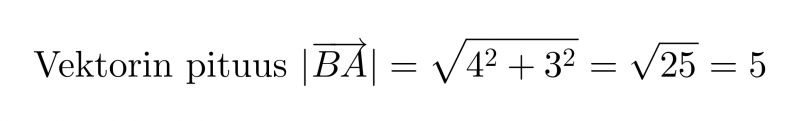
Klikkaa kuva suuremmaksi!
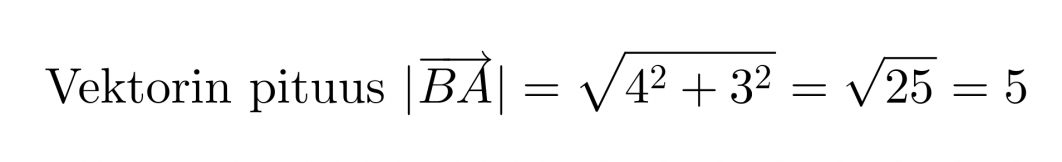
Klikkaa kuva suuremmaksi!
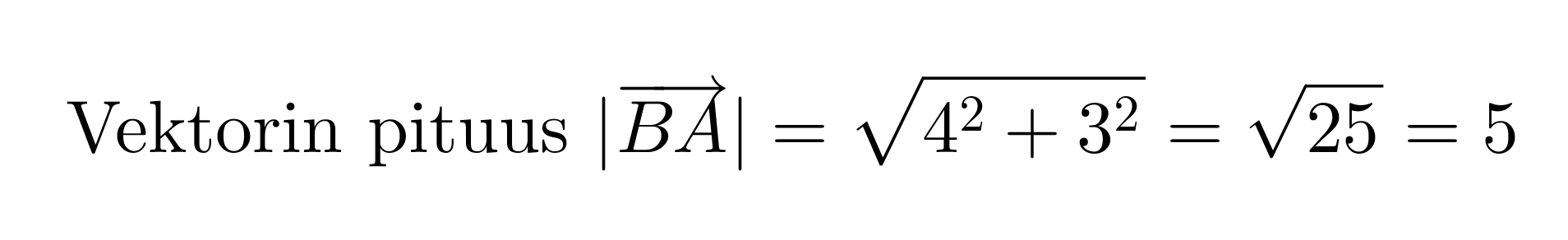
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Sievennetään vektorilausekkeet.
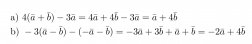
Klikkaa kuva suuremmaksi!
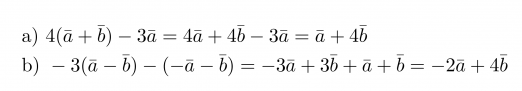
Klikkaa kuva suuremmaksi!
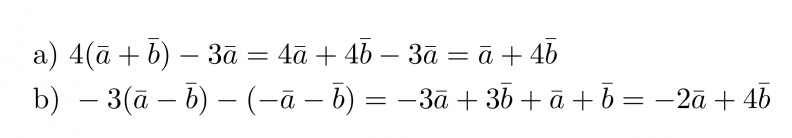
Klikkaa kuva suuremmaksi!
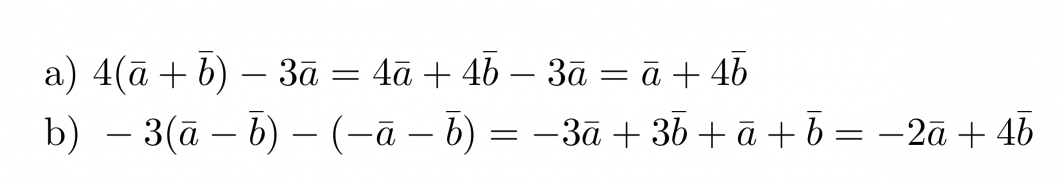
Klikkaa kuva suuremmaksi!
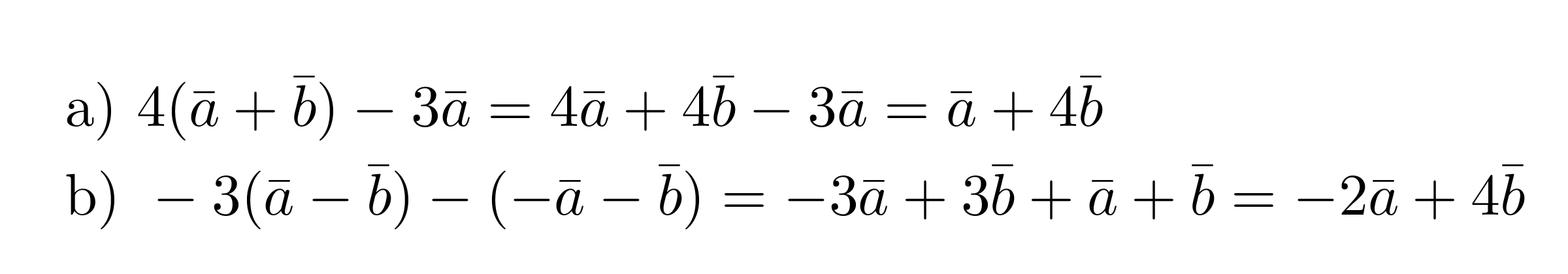
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Yhdensuuntaisten vektoreiden laskeminen yhteen ja vähentäminen toisistaan vastaa reaaliluvuilla laskemista. Erisuuntaisten vektoreiden yhdistämisessä on oltava tarkkana, sillä tällöin on huomioitava myös vektoreiden suunnat. Tähän perehdytään seuraavassa kappaleessa.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014