19. Vektoreiden yhteenlasku*

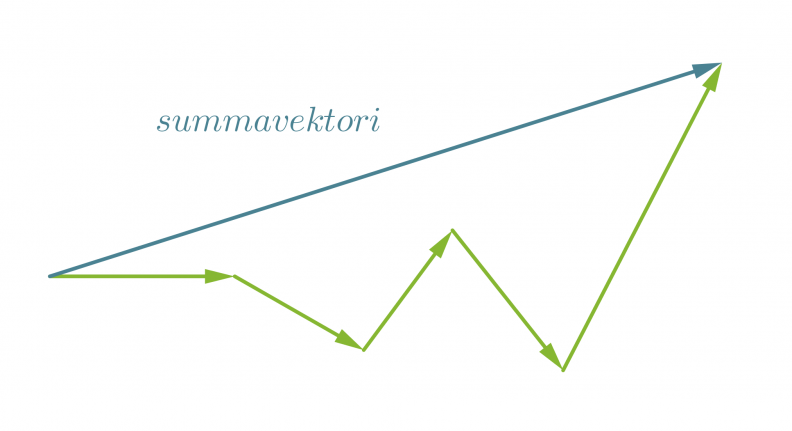
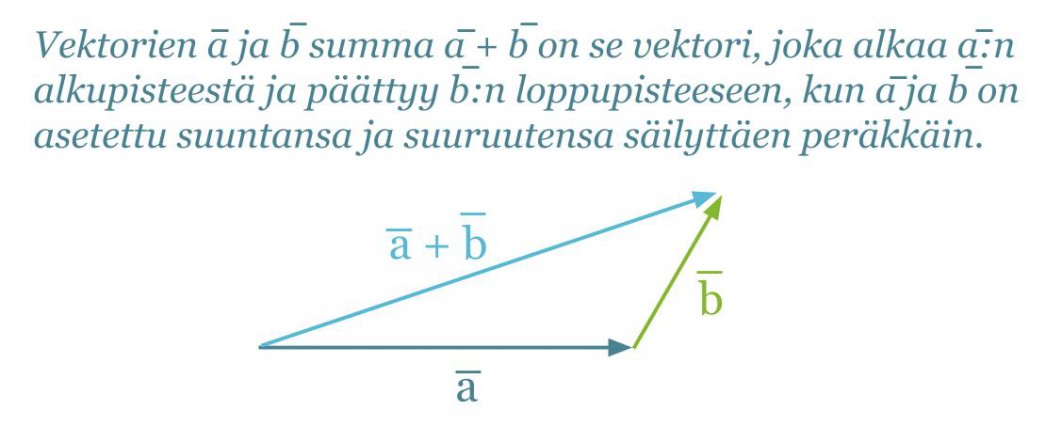
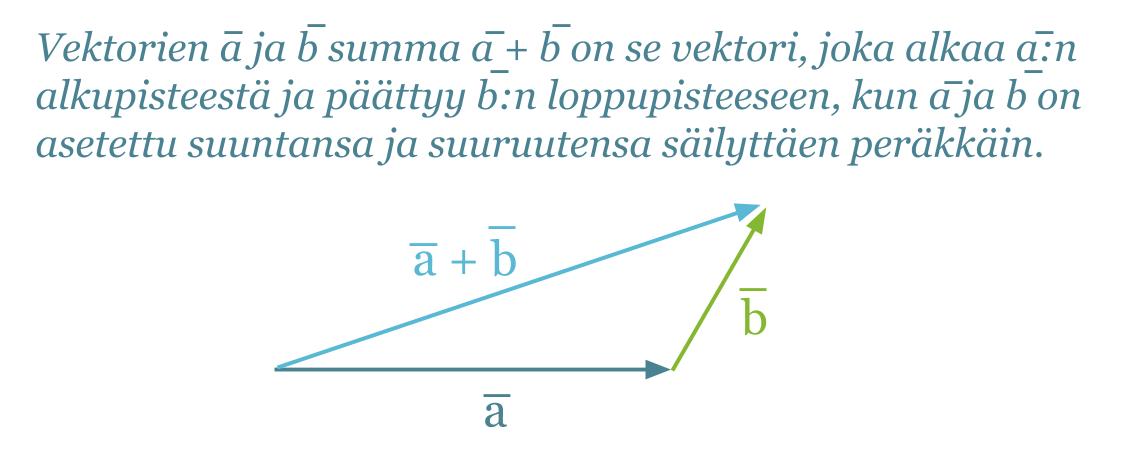
Vek­to­reil­le mer­kit­se­vää ovat ai­no­as­taan nii­den pi­tuus ja suun­ta, ei se, mis­sä ne ovat. Sik­si vek­to­rei­den paik­kaa voi­daan vaih­taa kun­han nii­den pi­tuus ja suun­ta säi­ly­te­tään. Vek­to­rei­ta las­ke­taan yh­teen si­ten, että vek­to­rit ase­te­taan pe­räk­käin suun­tan­sa ja suu­ruu­ten­sa säi­lyt­tä­en. Sum­ma­vek­to­ri on ly­hyin reit­ti en­sim­mäi­sen vek­to­rin alku­pis­tees­tä vii­mei­sen vek­to­rin lop­pu­pis­tee­seen.

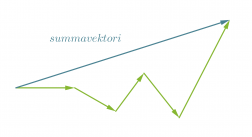
Klik­kaa kuva suu­rem­mak­si!

Vek­to­rit voi­daan aset­taa pe­räk­käin mis­sä jär­jes­tyk­ses­sä ta­han­sa, sil­lä vek­to­rien yh­teen­las­ku nou­dat­taa vaih­dan­ta­la­kia.

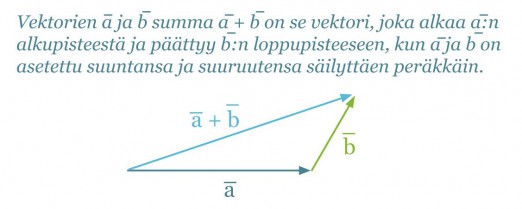
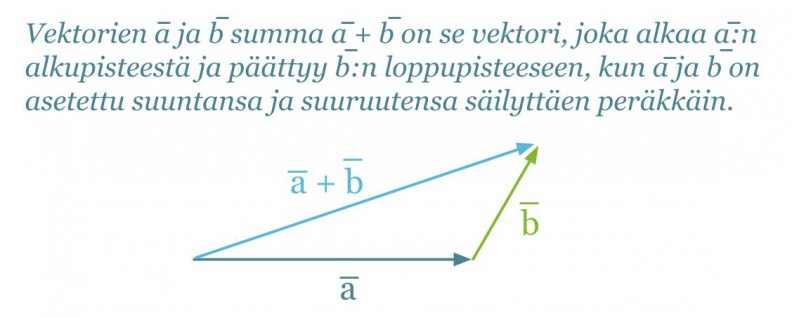
Klik­kaa kuva suu­rem­mak­si!

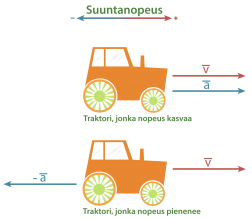
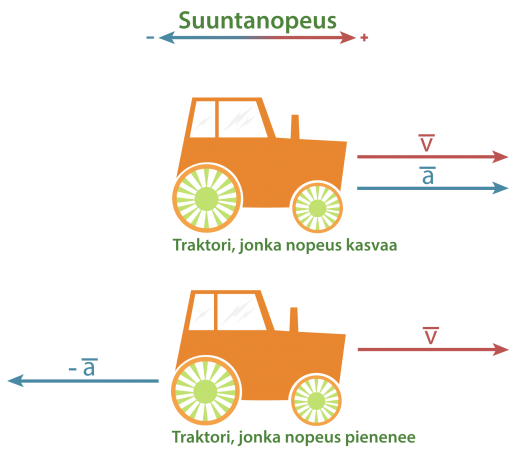
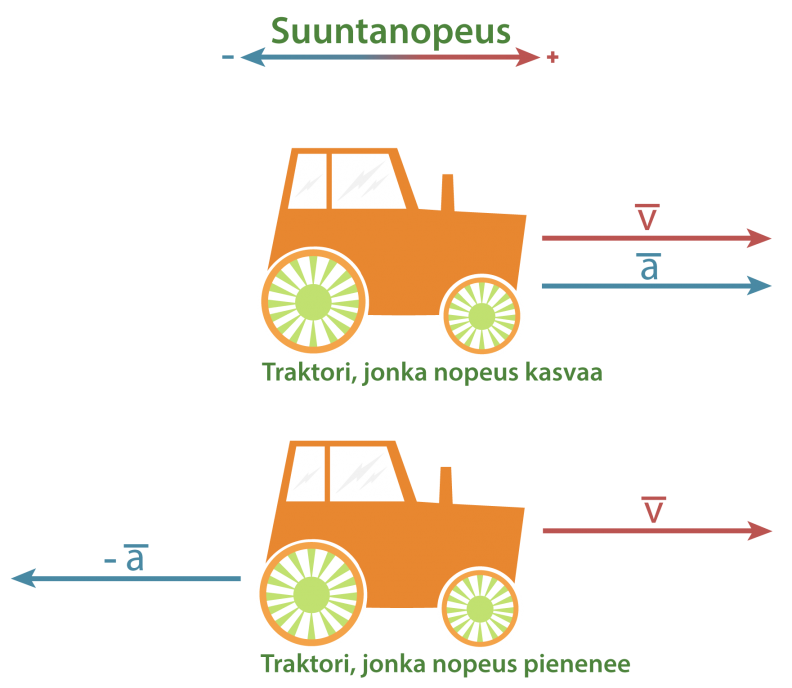
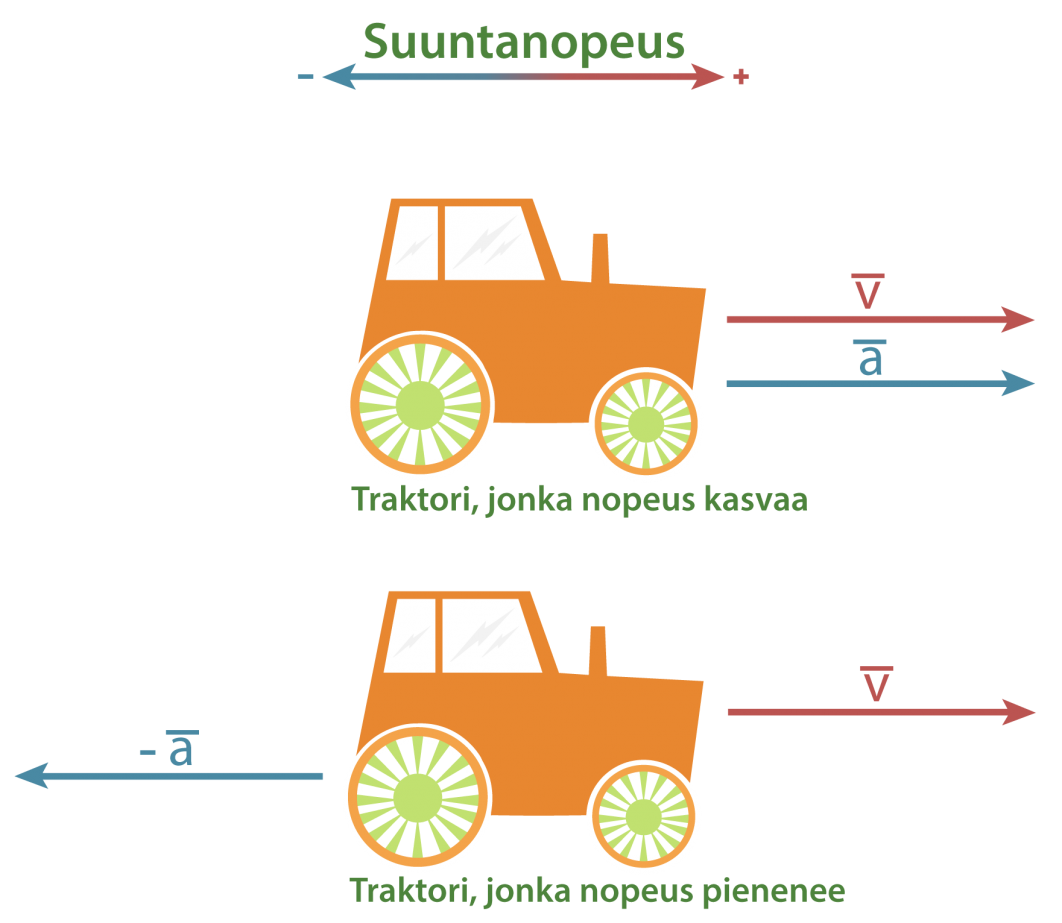
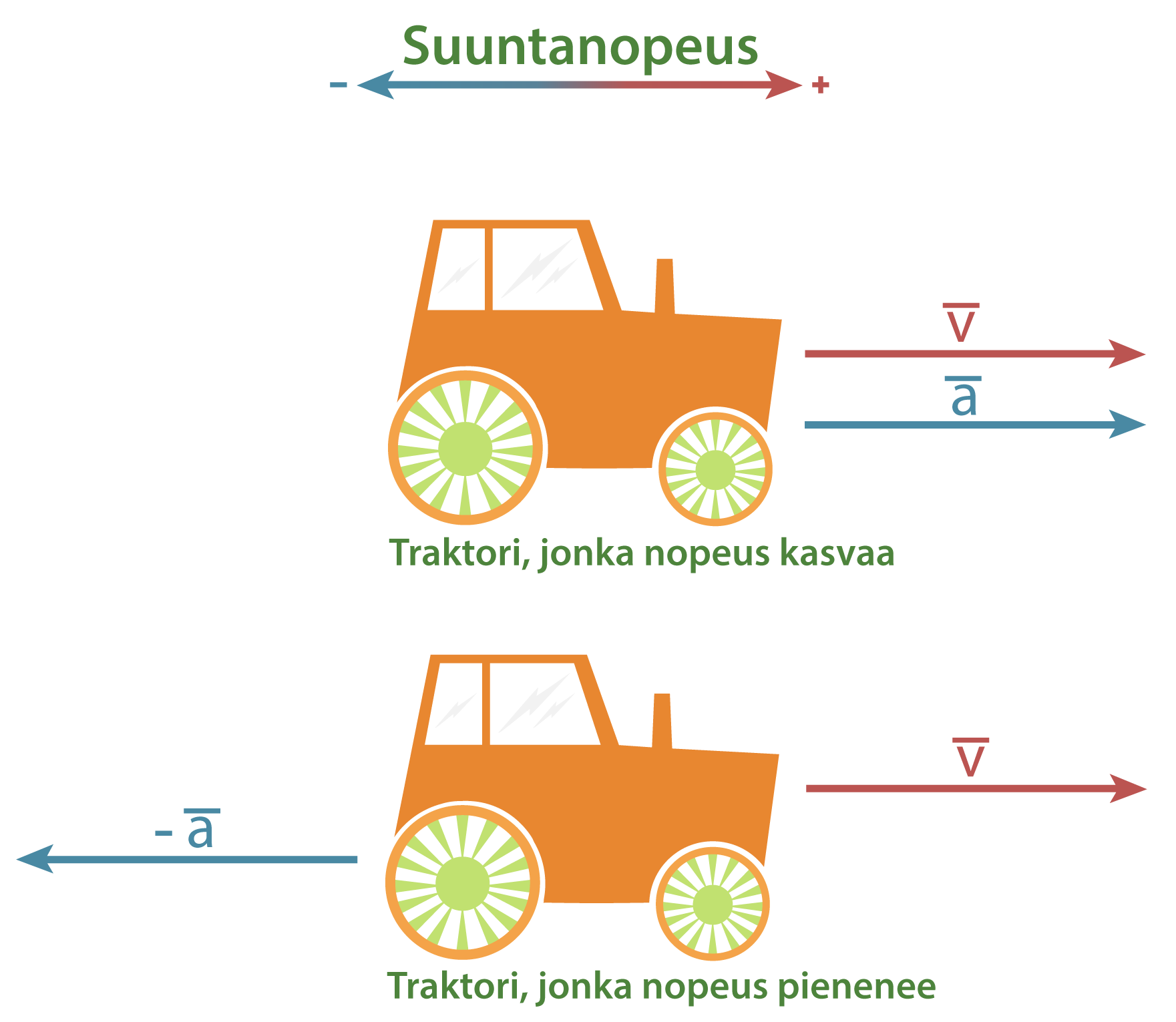
Kun tar­kas­tel­laan vek­to­rei­den avul­la esi­mer­kik­si no­peuk­sia, on teh­tä­vä aluk­si suun­ta­so­pi­mus. Las­kuis­sa va­rus­te­taan va­lit­tuun suun­taan osoit­ta­van vek­to­ri­suu­reen arvo plus­mer­kil­lä ja vas­tak­kai­seen suun­taan osoit­ta­van mii­nus­mer­kil­lä. Suun­ta­so­pi­mus teh­dään yleen­sä si­ten, että las­kut voi­daan suo­rit­taa po­si­tii­vi­sil­la lu­vuil­la.

Klik­kaa kuva suu­rem­mak­si!

Kiih­ty­vyys on vek­to­ri­suu­re, joka suo­ra­vii­vai­ses­sa liik­kees­sä on sa­man­suun­tai­nen tai vas­tak­kais­suun­tai­nen no­peu­teen näh­den. No­peut­taan li­sää­vän trak­to­rin kiih­ty­vyys on no­peu­den suun­tai­nen, mut­ta hi­das­tu­van trak­to­rin kiih­ty­vyys on no­peu­del­le vas­tak­kai­nen.

Esimerkki 1.

Lai­va sei­laa koh­ti länt­tä no­peu­del­la 60 km/h. Yl­lät­tä­en sii­hen vai­kut­taa ete­lä­tuu­li, jon­ka no­peus on 20 km/h. Mikä on lai­van uusi kul­ku­suun­ta ja no­peus?

Ratkaisu:

Ti­lan­net­ta voi­daan ha­vain­nol­lis­taa vek­to­reil­la. Va­li­taan po­si­tii­vi­sik­si suun­nat ete­läs­tä poh­joi­seen ja idäs­tä län­teen. Vek­to­rei­den pi­tuu­det ku­vaa­vat no­peu­den suu­ruut­ta.

Klik­kaa kuva suu­rem­mak­si!

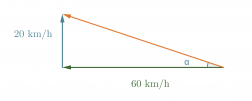
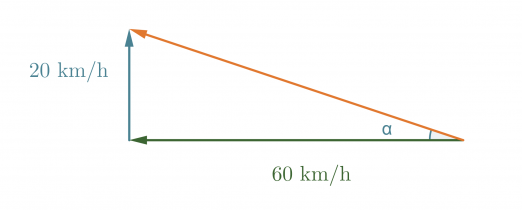
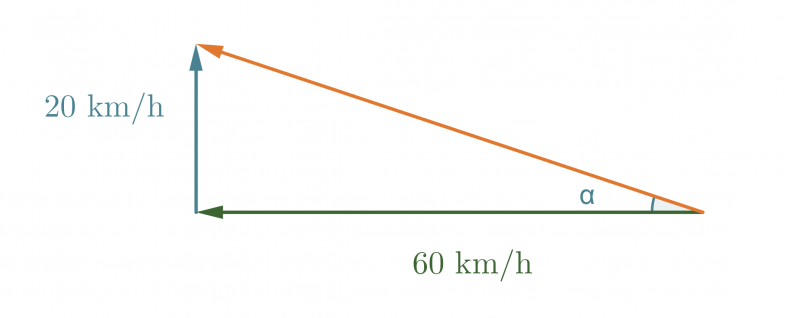
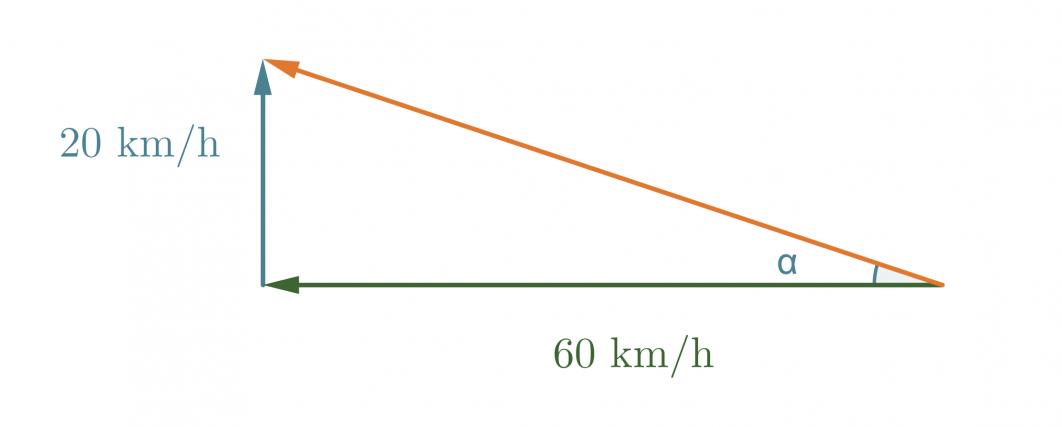
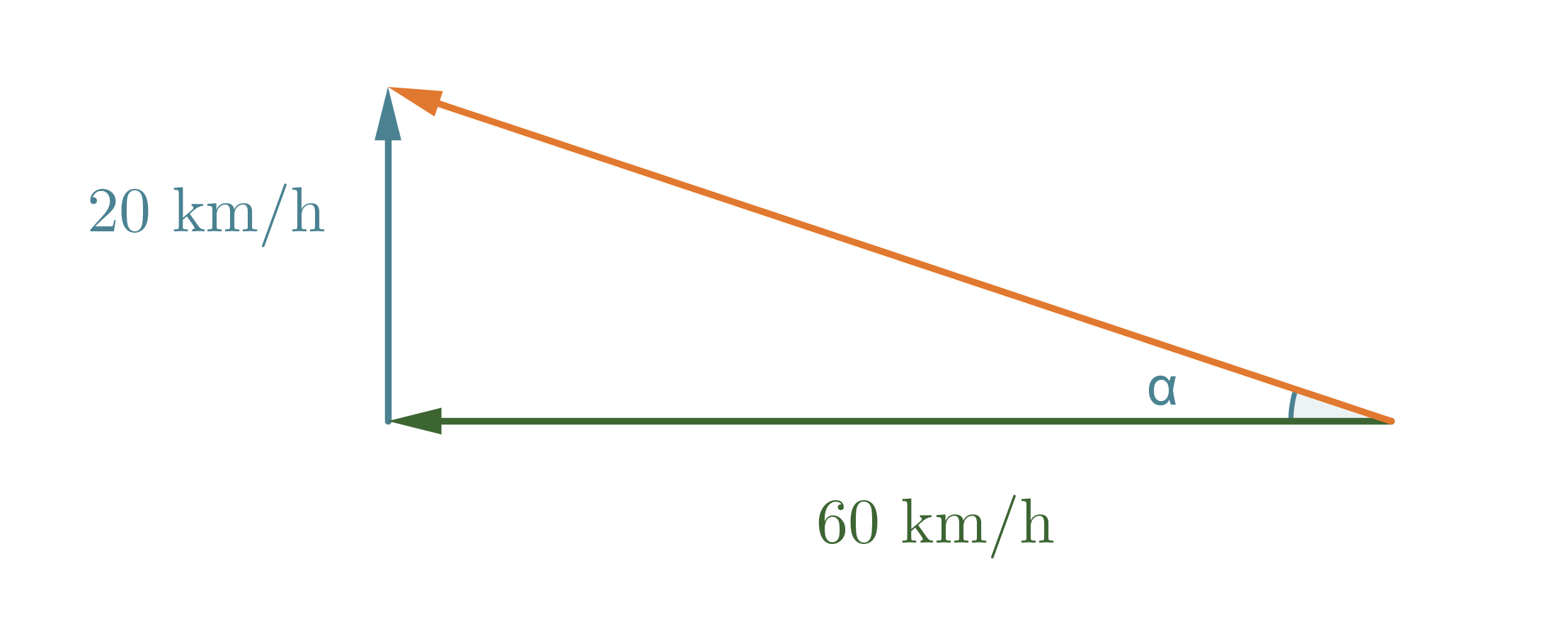
Nämä kak­si vek­to­ria vai­kut­ta­vat siis lai­van no­peu­teen ja kul­ku­suun­taan. Yh­teis­vai­ku­tus saa­daan las­ke­mal­la vek­to­rit yh­teen.

Klik­kaa kuva suu­rem­mak­si!

Ku­van pu­nai­nen vek­to­ri ku­vaa ky­syt­tyä no­peut­ta, sen pi­tuus saa­daan sel­vil­le Py­tha­go­raan lau­seen avul­la

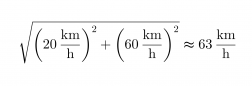
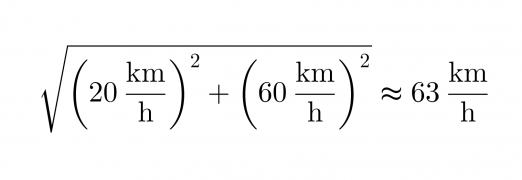
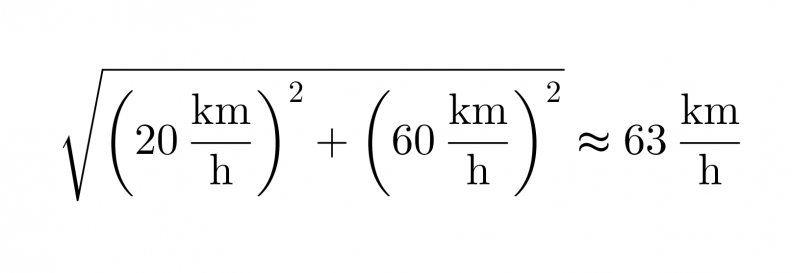
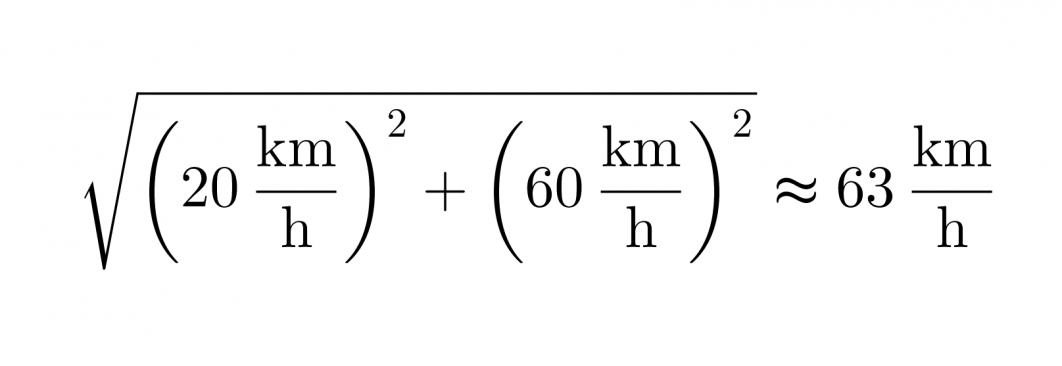
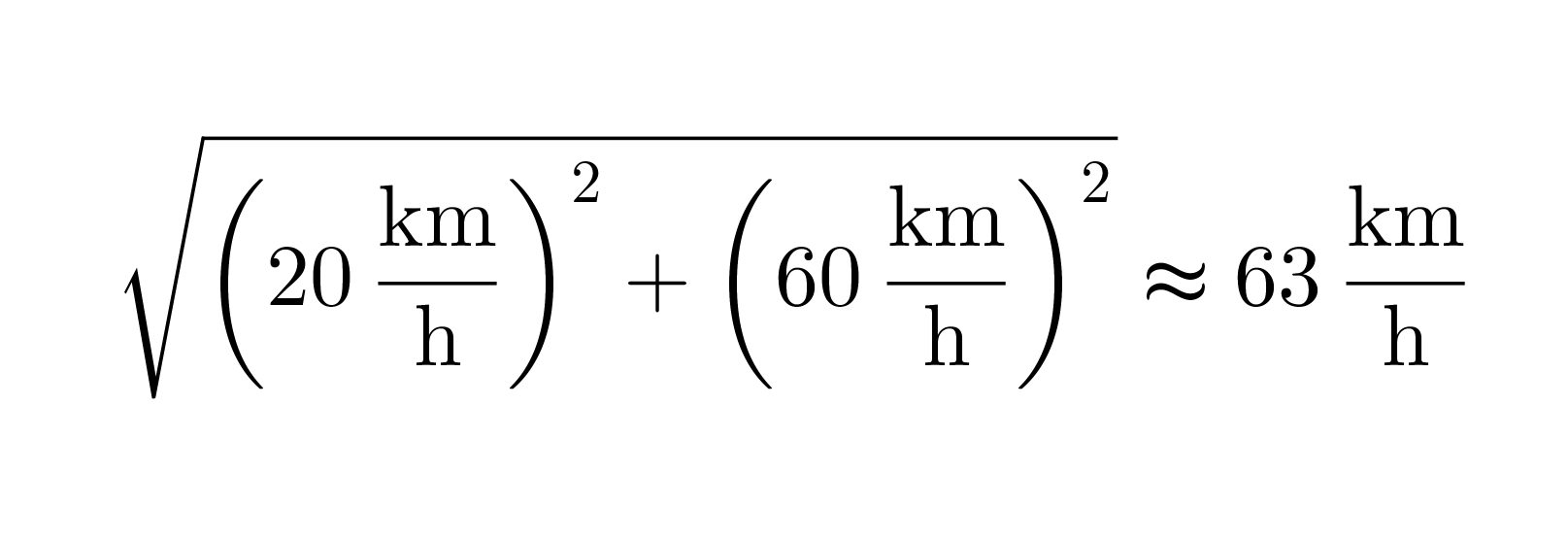
Klik­kaa kuva suu­rem­mak­si!

ja kul­ma α tan­gen­tin avul­la

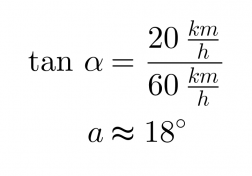
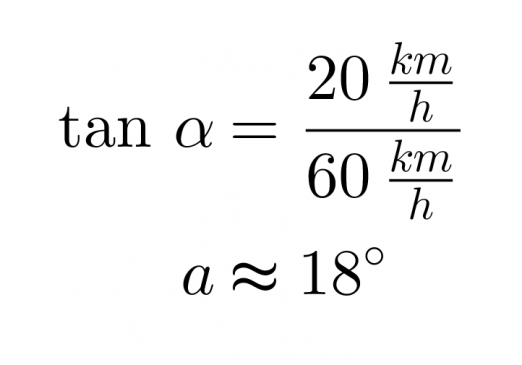
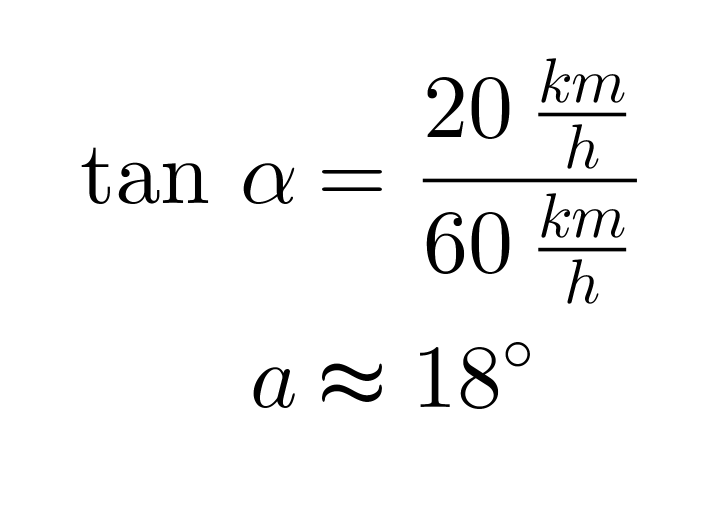
Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Lai­van uusi no­peus on 63 km/h ja suun­ta muut­tuu alku­pe­räi­ses­tä 18° koh­ti poh­jois­ta.