4. Tilastomuuttujan tyypit ja frekvenssi

Ti­las­to­ku­vaa­jan eli dia­gram­min tyyp­pi va­li­taan sen mu­kaan mil­lai­nen ti­las­to­muut­tu­ja on ky­sees­sä.

Dis­kreet­tiä muut­tu­jaa ku­va­taan yleen­sä pyl­väs­dia­gram­min avul­la. Jat­ku­vaa muut­tu­jaa ku­va­taan sen si­jaan yleen­sä viivadigrammilla tai his­to­gram­mil­la. Dis­kree­tin ti­las­to­muut­tu­jan ar­vot voi­daan las­kea. Jat­ku­van ti­las­to­muut­tu­jan ar­vot voi­daan mi­ta­ta.

Frek­vens­si voi­daan il­mais­ta myös pro­sent­tei­na koko­nais­mää­räs­tä, jol­loin käy­te­tään ni­mi­tys­tä suh­teel­li­nen frek­vens­si. Suh­teel­li­sien frek­vens­sien ha­vain­nol­lis­ta­mi­seen so­pii hy­vin sek­to­ri­dia­gram­mi.

Suh­teel­lis­ten frek­vens­sien sum­ma on aina 1 tai 100 %, las­kuis­sa sum­ma voi hie­man poi­ke­ta joh­tu­en pyö­ris­tyk­sis­tä.

Esimerkki 1

Luo­kan op­pi­lai­den si­sa­rus­ten luku­mää­rää ku­vaa­va ti­las­to on seu­raa­va:

2 1 2 3 0 1 0 4 3 4 2 1 1 3 2 2

Ti­las­to­muut­tu­ja on täs­sä ta­pauk­ses­sa si­sa­rus­ten luku­mää­rä ja ky­sees­sä on dis­kreet­ti muut­tu­ja, kos­ka si­sa­rus­ten luku­mää­rä saa­daan sel­vil­le las­ke­mal­la.

Ryh­mi­tel­lään tie­dot si­sa­rus­ten luku­mää­räs­tä. Mer­ki­tään tau­luk­koon kuin­ka mo­nel­la ei ole si­sa­ruk­sia, kuin­ka mo­nel­la on 1 si­sa­rus jne. Näin saa­daan sel­vil­le si­sa­rus­ten luku­mää­rien frek­vens­sit. Suh­teel­li­nen frek­vens­si puo­les­taan il­moit­taa, mo­nel­la­ko pro­sen­til­la koko luo­kan op­pi­lais­ta on tiet­ty mää­rä si­sa­ruk­sia.

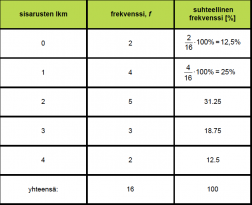
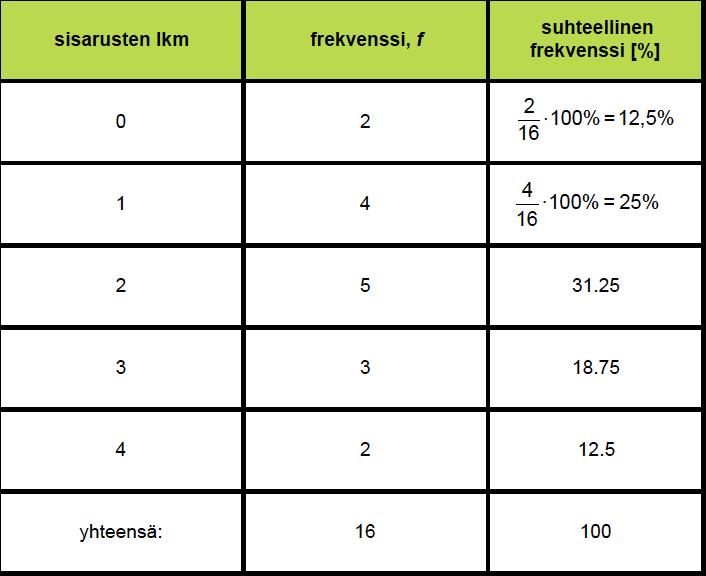
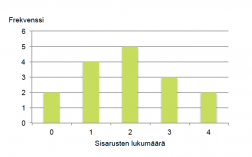
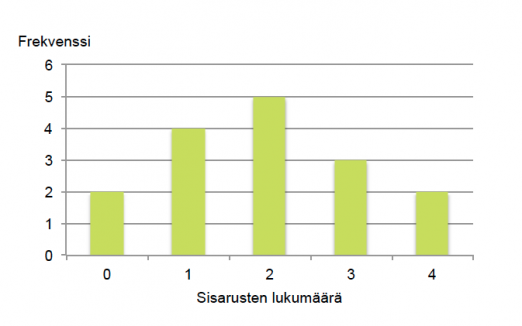
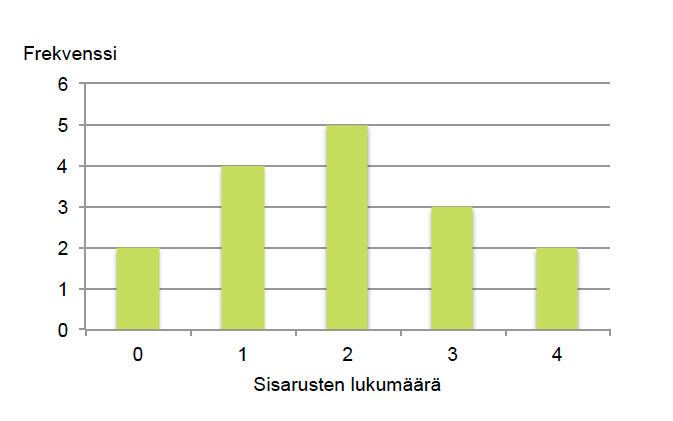
Frek­vens­sien pe­rus­teel­la voi­daan piir­tää pyl­väs­dia­gram­mi.

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

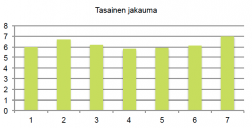
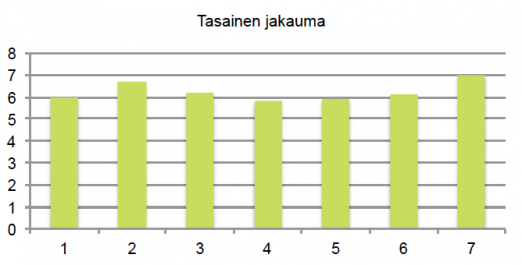
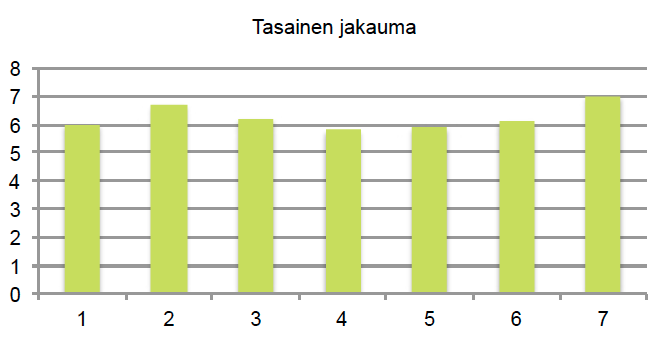
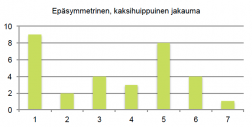
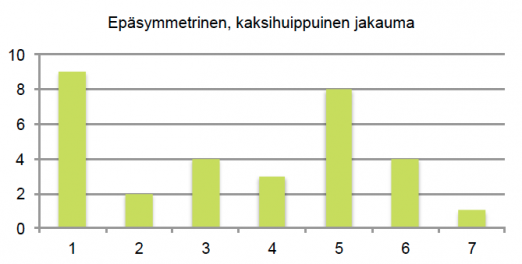
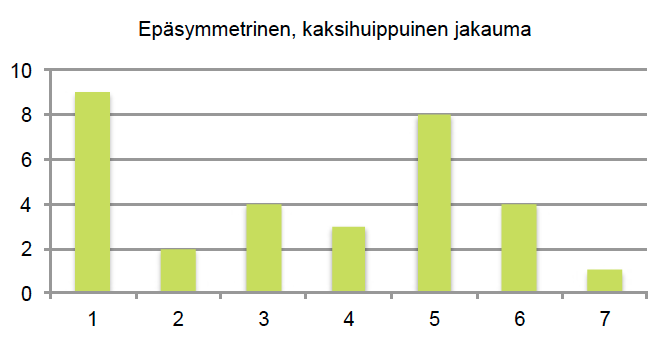
Esi­mer­kis­sä 1 pyl­väs­dia­gram­mi si­säl­tää kai­ken alku­pe­räi­sen in­for­maa­ti­on. Se on kui­ten­kin pal­jon ha­vain­nol­li­sem­pi tapa si­sa­rus­ten luku­mää­rän ku­vaa­mi­seen kuin pelk­kä tau­lu­koin­ti. Pyl­väs­dia­gram­mis­ta näh­dään li­säk­si, että si­sa­ruk­sien luku­mää­rän ja­kau­man ku­vaa­ja on yksi­huip­pui­nen ja se las­kee lä­hes sym­met­ri­ses­ti hui­pun kum­mal­la­kin puo­lel­la. Ja­kau­man ku­vaa­ja voi olla myös epä­sym­met­ri­nen tai moni­huip­pui­nen.

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

KES­KUS­TE­LU1: Ker­ro mitä ti­las­to­tie­to­ja si­nus­ta on vuo­sien var­rel­la ke­rät­ty? Mit­kä näis­tä tie­dois­ta ovat jul­ki­sia? Klik­kaa it­se­si kes­kus­te­luun klik­kaa­mal­la ala­puo­lel­la ole­vaa “Kes­kus­te­le ai­hees­ta” -ku­vaa ja muis­ta että saat pis­tei­tä myös kes­kus­te­luun osal­lis­tu­mi­ses­ta!

KES­KUS­TE­LU2: Mitä ti­las­to­tie­to­ja voit löy­tää sa­no­ma­leh­dis­tä? Mitä niis­sä on ti­las­to­muut­tu­ji­na? Mikä niis­sä on pe­rus­jouk­ko­na?Klik­kaa it­se­si kes­kus­te­luun klik­kaa­mal­la ala­puo­lel­la ole­vaa “Kes­kus­te­le ai­hees­ta” -ku­vaa ja muis­ta että saat pis­tei­tä myös kes­kus­te­luun osal­lis­tu­mi­ses­ta!