8. Hajontalukujen määrittäminen
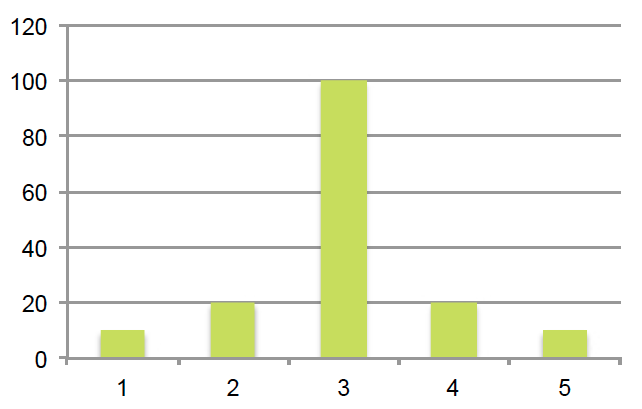
Alla esitetyillä kahdella erityyppisellä jakaumalla on sama mediaani. Pelkät keskiluvut eivät siis riitä jakaumien kuvailuun, vaan vaaditaan myös hajontalukuja, jotka kuvaavat miten tilastomuuttujan arvot jakautuvat tai hajaantuvat arvoasteikolle.
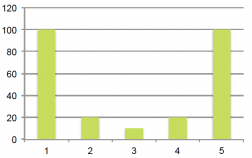
Klikkaa kaaviota suurentaaksesi!
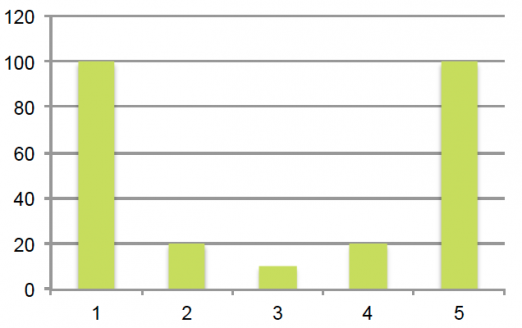
Klikkaa kaaviota suurentaaksesi!
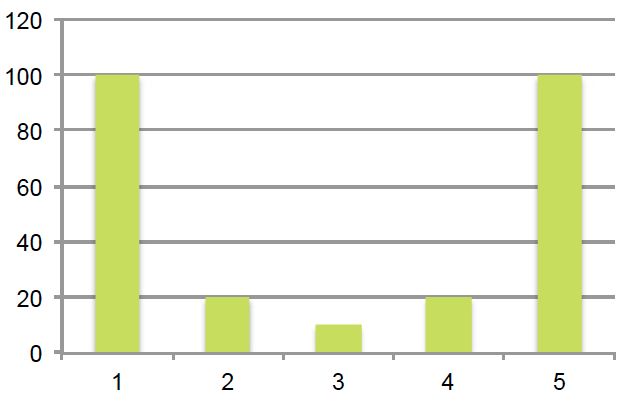
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
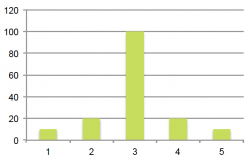
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
Vaihteluväli kertoo millä välillä havainnot vaihtelevat. Vaihteluvälin pituus on muuttujan suurimman ja pienimmän arvon erotus.
Hajontaluvut kuvaavat aineiston vaihtelua keskikohdasta mitattuna. Hajontalukuja ovat mm. vaihteluväli, vaihteluvälin pituus ja keskihajonta. Näistä jälkimmäinen on yleisin.
Esimerkki 1
Lukujonon 100, 76, 23, 636, 9, 94, 91, 555 vaihteluväli on (9, 555) ja vaihteluvälin pituus on 555 – 9 = 546.
Keskihajonta ilmoittaa, kuinka kaukana muuttujan arvot ovat keskimäärin keskiarvosta.
Esimerkki 2
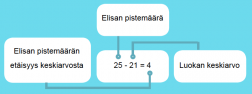
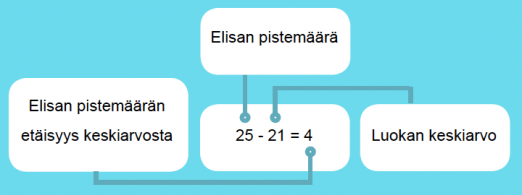
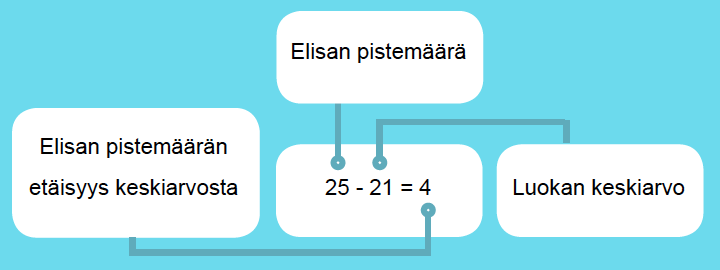
Elisa sai historian kokeesta 25 pistettä. Luokan keskiarvo oli 21 ja keskihajonta 5. Rinnakkaisluokalla oleva Petteri sai kokeesta 28 pistettä. Petterin luokan keskiarvo oli 24 ja keskihajonta 6. Tutkitaan, kumman koetulos oli omaan luokkaansa verrattuna parempi.
Elisan koetulos:
Klikkaa kaaviota suurentaaksesi!
Klikkaa kaaviota suurentaaksesi!
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
Verrataan saatua erotusta nyt keskihajontaan, niin saadaan selville kuinka monta hajontaa keskiarvon yläpuolella Elisan pistemäärä on: 4/5 = 0,8
Vastaavasti Petterin koetulos:
28 – 24 = 4
4/6 ≈ 0,67
Vastaus: Elisan tulos on suhteellisesti parempi.
Windows-laskimella saadaan keskihajonta laskettua kätevästi. Luvut syötetään samoin kuin keskiarvoakin laskettaessa. Kun kaikki luvut on syötetty ja klikattu Sta-painiketta, saadaan keskihajonta klikkaamalla tilastonäppäintä s.
Avoin matematiikkaTilastoja ja todennäköisyyksiä4.4.2013