12. Todennäköisyyden määrittäminen
Myrphyn laista kiinnostunut tutkija halusi selvittää, putoaako voileipä lattialle todennäköisemmin voipuoli alaspäin. Hän pudotti voileivän lattialle 100 kertaa, joista 57 kertaa leipä putosi voipuoli alaspäin. Näin hän sai lasketuksi tapahtuman todennäköisyyden:
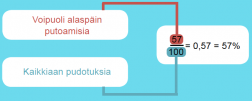
Klikkaa kaaviota suurentaaksesi!
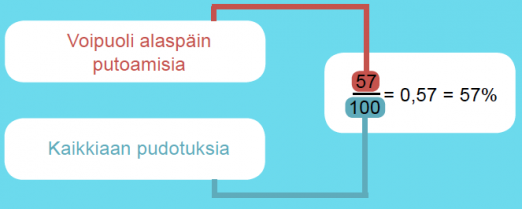
Klikkaa kaaviota suurentaaksesi!
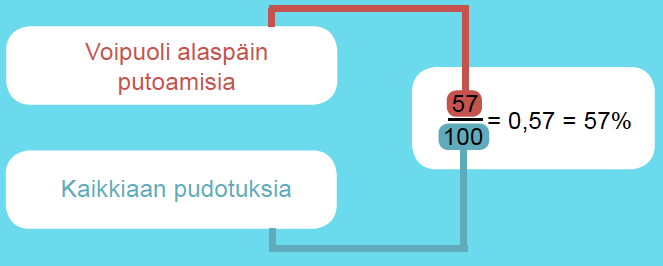
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
Todennäköisyyksiä voidaan siis selvittää koejärjestelyjen avulla. Sitä todenmukaisempi tulos saadaan, mitä useammin koe suoritetaan. Esimerkiksi leipä saattaa pudota aluksi viisi kertaa peräkkäin voipuoli alaspäin. Jos koe suoritetaan ainoastaan viisi kertaa, saadaan tulokseksi, että voipuoli koskettaa aina lattiaa. Todennäköisyyksissä on kyse sattumista ja tämän vuoksi koe täytyy toistaa useita kertoja, jotta tulos olisi luotettava. On mahdollista, että seuraavilla viidellä pudotuskerralla ei tarvitse pyyhkiä voita lattiasta.
Todennäköisyyksiä voidaan tarkastella neljällä eri tavalla. Tavat eivät ole toisiaan poissulkevia ja joihinkin tarkasteluihin sopiikin niistä useampi kuin yksi. Mitä tavoista on käytetty voileipäongelmassa?
- Käytetään hyväksi symmetriaa. Todennäköisyys, että saadaan nopalla heitettäessä kuusi on 1/6 , sillä nopassa on kuusi tahkoa, joista päällimmäiseksi voi jäädä mikä tahansa.
- Suoritetaan kokeita tai tarkasteluja tietojen keräämiseksi. Jos halutaan selvittää, millä todennäköisyydellä ohi ajava auto on punainen, pysähdytään kadunkulmaan ja lasketaan kaikkien ohi ajavien autojen lukumäärä sekä näistä punaisten osuus.
- Katsotaan tapahtumia menneisyydestä. Saapuuko juna asemalle todennäköisesti myöhässä? Katsotaan aikaisempia saapumisia, esimerkiksi kahden viime viikon ajalta ja lasketaan kuinka monesta niistä juna tuli myöhässä.
- Tehdään omakohtainen arvio. Tätä menetelmää käytetään silloin, kun koe ei ole toistettavissa eli mitään muuta aikaisemmin esitettyä tavoista ei voi käyttää. Millä todennäköisyydellä Suomi voittaa kultaa seuraavissa jääkiekon MM-kisoissa? Tarkastellaan viime vuosien otteluita sekä tämän kauden voittoja, joiden perusteella yritetään luoda realistisen arvio voittomahdollisuudelle.