14. Tilastollinen ja geometrinen todennäköisyys

Esimerkki 1.

Mi­ten voi­daan las­kea syn­ty­vän lap­sen suku­puo­len to­den­nä­köi­syys, kun ta­pah­tu­ma ei ole sym­met­ri­nen? Poi­kia ni­mit­täin syn­tyy enem­män kuin tyt­tö­jä niin Suo­mes­sa kuin muu­al­la­kin maa­il­mas­sa.

Ratkaisu:

Suo­men ti­las­tol­li­sen vuo­si­kir­jan (1998) mu­kaan vuo­si­na 1990-1997 Suo­mes­sa syn­tyi 510 851 las­ta, jois­ta tyt­tö­jä oli 250 227. Tyt­tö­jen osuus tä­män pe­rus­teel­la on 250 227 / 510 851 ≈ 0,4889 ≈ 49%

Voi­daan olet­taa, että tyt­tö­jen osuus säi­lyy tu­le­vai­suu­des­sa­kin sa­ma­na, jo­ten
P(seu­raa­va Suo­mes­sa syn­ty­vä lap­si on tyt­tö) = 49 %

Ti­las­tol­li­nen to­den­nä­köi­syys liit­tyy ta­pah­tu­miin, joi­ta voi­daan se­lit­tää joko ti­las­to­jen tai ko­keel­lis­ten ha­vain­to­jen avul­la.

Ge­o­met­ri­nen to­den­nä­köi­syys las­ke­taan ku­ten klas­si­nen to­den­nä­köi­syys, mut­ta sii­nä ver­ra­taan toi­siin­sa ge­o­met­ri­sia ku­vi­oi­ta, ku­ten ja­no­jen pi­tuuk­sia, alu­ei­den pin­ta-alo­ja ja kap­pa­lei­den ti­la­vuuk­sia.

Esimerkki 2

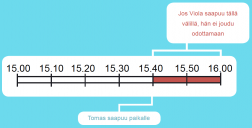
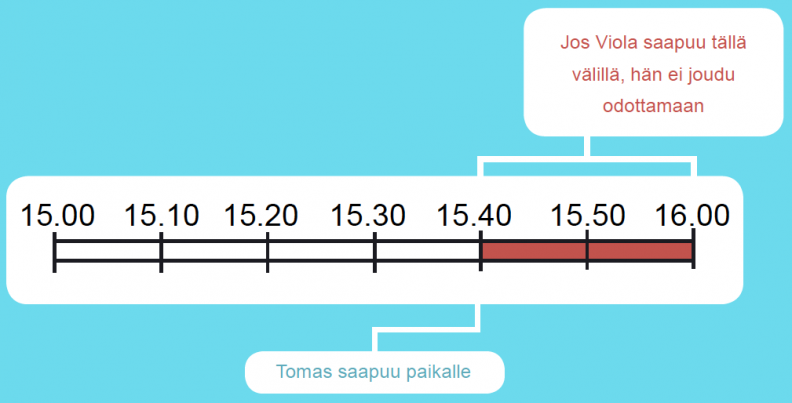
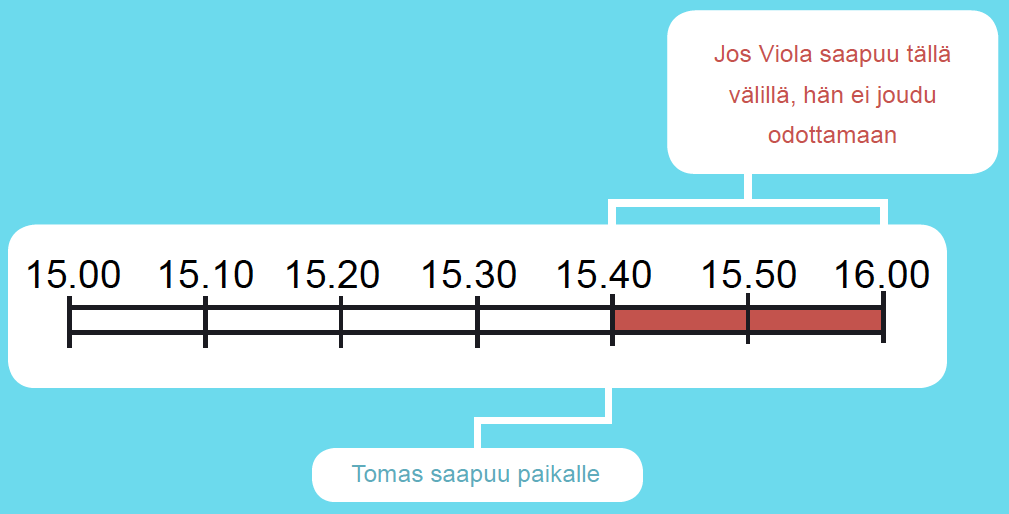
Vi­o­la on so­pi­nut ta­paa­van­sa Tomaksen kah­vi­las­sa klo: 15.00 ja klo: 16.00 vä­lil­lä. Tomas saa­puu pai­kal­le klo: 15.40. Mil­lä to­den­nä­köi­syy­del­lä Vi­o­la ei jou­du odot­ta­maan?

Ratkaisu:

Tun­nis­sa on ää­re­tön mää­rä ajan­het­kiä, jo­ten nii­den kaik­kien lu­et­te­le­mi­nen ei ole mah­dol­lis­ta. Pe­rus­jouk­koa ja al­keis­ta­pah­tu­mia on tar­kas­tel­ta­va nyt ge­o­met­ri­ses­ti.

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

P(Vi­o­la ei jou­du odot­ta­maan) = 20min / 60min = 1/3 ≈ 0,33

Vas­taus: To­den­nä­köi­syys on 0,33