15. Malleja alkeistapausten muodostamiseksi

To­den­nä­köi­syyk­siä las­ket­ta­es­sa on sel­vi­tet­tä­vä suo­tuis­ten ja kaik­kien al­keis­ta­paus­ten luku­mää­rä. Jos al­keis­ta­pauk­sia on pal­jon, on nii­den lu­et­te­le­mi­nen työ­läs­tä. Al­keis­ta­paus­ten luku­mää­rän sel­vit­tä­mi­sek­si on­kin ke­hi­tet­ty eri­lai­sia me­ne­tel­miä.

Esimerkki 1

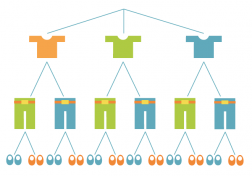
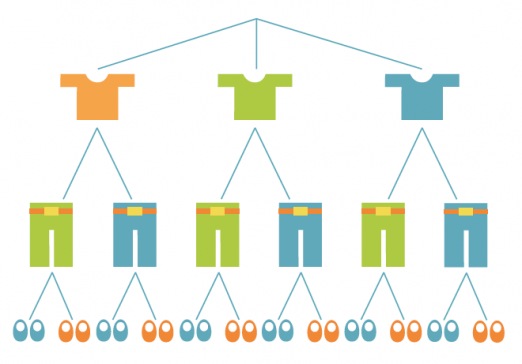
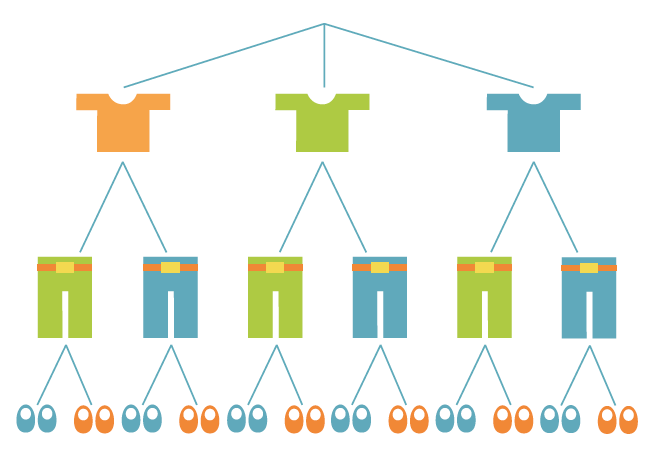
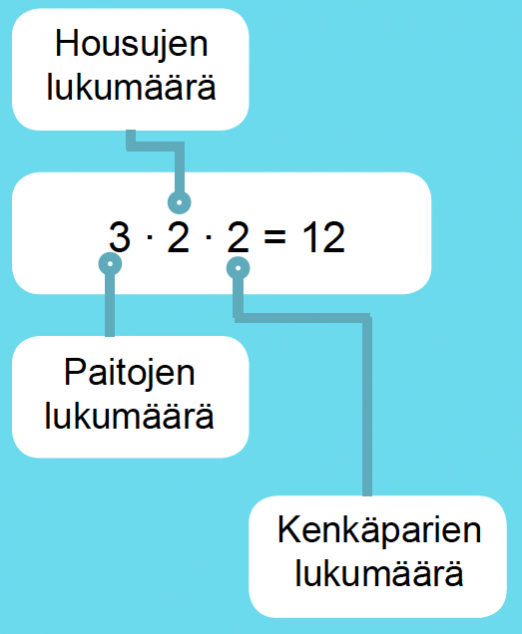
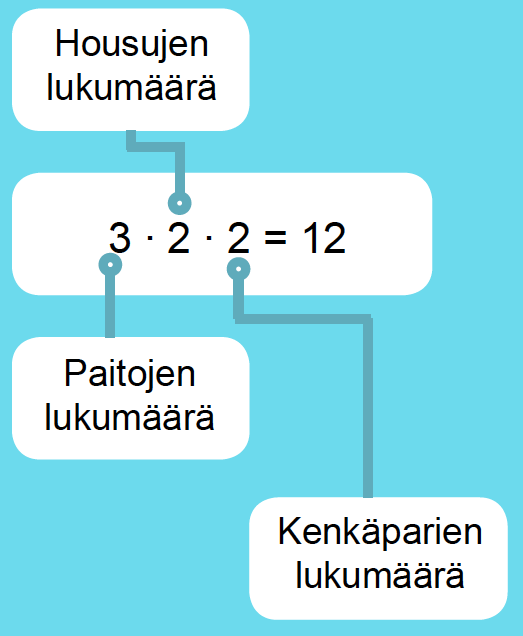
Mii­sal­la on loma­mat­kal­la mu­ka­na kol­me pai­taa, kah­det hou­sut ja kak­si pa­ria ken­kiä. Las­ke­taan, mon­ta­ko asu­ko­ko­nai­suut­ta hän voi niis­tä muo­dos­taa.

Ti­lan­net­ta voi­daan ha­vain­nol­lis­taa puu­dia­gram­min avul­la. Yksi reit­ti lat­vas­ta juu­reen ku­vaa yhtä al­keis­ta­paus­ta. Puu­dia­gram­mis­ta näh­dään, että eri­lai­sia asu­ko­ko­nai­suuk­sia on yh­teen­sä 12 kpl.

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

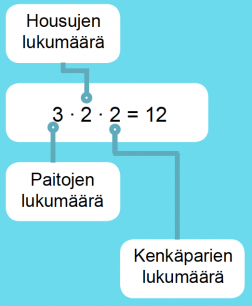
Sama tu­los saa­daan myös ker­to­las­kul­la: 3 ∙ 2 ∙ 2 = 12

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

Ky­syt­ty asu­ko­ko­nai­suuk­sien luku­mää­rä saa­tiin siis ker­to­mal­la kes­ke­nään eri vai­heis­sa ole­vien vaih­to­eh­to­jen luku­mää­rät. Peri­aa­tet­ta sa­no­taan tulo­peri­aat­teek­si.

Esimerkki 2

Las­ke­taan, mo­nel­la­ko eri ta­val­la kol­me hen­ki­löä A, B ja C voi­vat aset­tua ri­viin.

Ri­vin en­sim­mäi­nen hen­ki­lö voi­daan va­li­ta kol­mel­la eri ta­val­la, toi­nen hen­ki­lö kah­del­la eri ta­val­la ja kol­mas hen­ki­lö yh­del­lä ta­val­la. Jo­ten hen­ki­löt voi­vat aset­tua ri­viin 3 • 2 • 1 = 6 eri ta­val­la.

Esimerkki 3

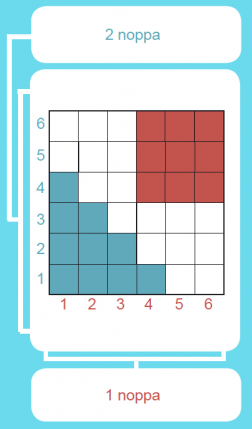
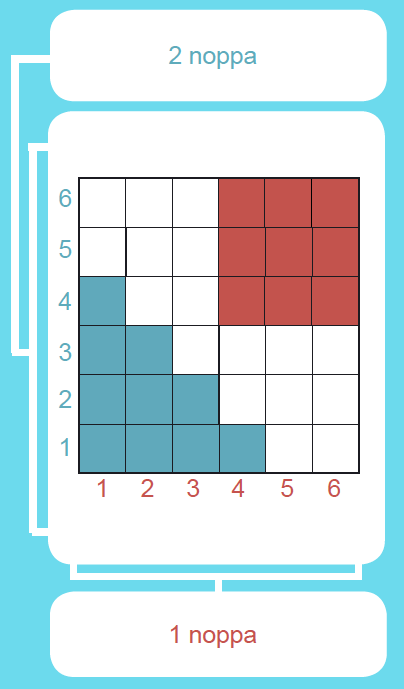
Hei­te­tään kah­ta nop­paa. Mil­lä to­den­nä­köi­syy­del­lä

1. kum­mas­sa­kin no­pas­sa on pis­te­lu­ku­na vä­hin­tään 4
2. pis­te­lu­ku­jen sum­ma on enin­tään 5?

Ratkaisu:

Käy­te­tään ruu­duk­koa ti­lan­teen ha­vain­nol­lis­ta­mi­seen. Ruu­dut ku­vaa­vat al­keis­ta­pauk­sia ja nii­tä on kaik­ki­aan 36 kpl.

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

1. Suo­tui­sia pa­re­ja on 9 kpl (ruu­du­kos­sa pu­nai­sel­la), jo­ten P(kum­mas­sa­kin no­pas­sa vä­hin­tään 4) = 9/36 = 1/4 = 0,25.
2. Suo­tui­sia pa­re­ja on nyt 10 kpl (ruu­du­kos­sa si­ni­sel­lä), jo­ten P(pis­te­lu­ku­jen sum­ma enin­tään 5) = 10/36 = 5/18 ≈ 0,28.

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!