16. Riippumattomien tapahtumien kertosääntö

Ker­to­las­ku ja yh­teen­las­ku ovat to­den­nä­köi­syys­las­ken­nan pe­rus­las­ku­toi­mi­tuk­sia. Ker­to­las­kun avul­la las­ke­taan to­den­nä­köi­syys use­an ta­pah­tu­man sa­man­ai­kai­sel­le esiin­ty­mi­sel­le. Yh­teen­las­kun avul­la puo­les­taan tar­kas­tel­laan sa­man sa­tun­nais­il­mi­ön eri­lai­sia ta­pah­tu­mis­mah­dol­li­suuk­sia.

Esi­mer­kik­si no­pan­hei­tos­sa saa­dut sil­mä­lu­vut ovat riip­pu­mat­to­mia toi­sis­taan. Nop­pa ei ”muis­ta” min­kä tu­lok­sen an­toi vii­mek­si ja jätä an­ta­mat­ta sa­maa pis­te­lu­kua.

Esimerkki 1

Hei­te­tään nop­paa nel­jä ker­taa. Las­ke­taan, mil­lä to­den­nä­köi­syy­del­lä saa­daan joka ker­ral­la sama pis­te­luku.

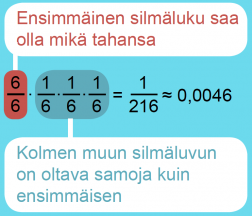
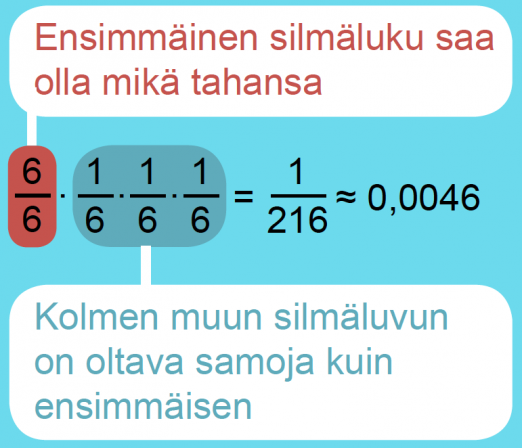
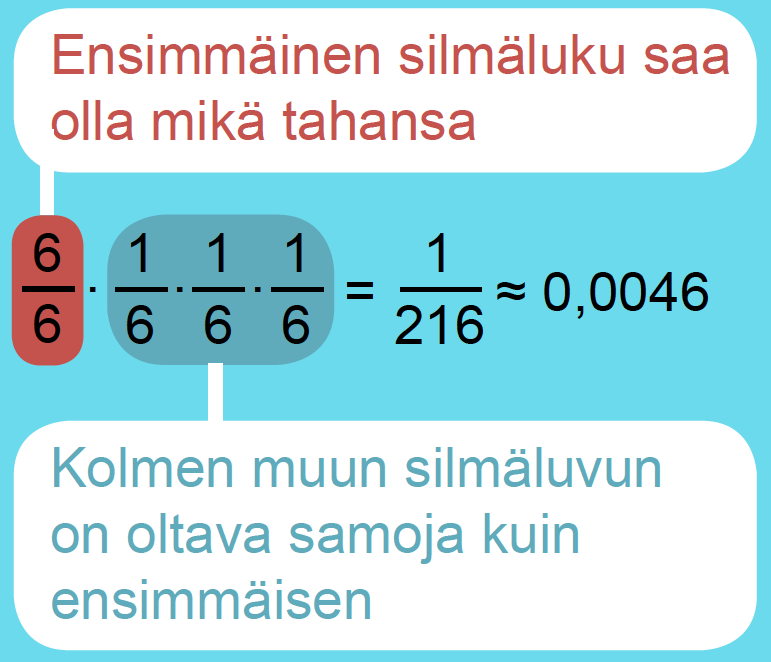
Esimerkki 2

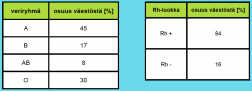
Ih­mi­set voi­daan ja­kaa ryh­miin ve­ren pe­rus­teel­la sen mu­kaan, mi­hin veri­ryh­mään (A, B, AB ja O) tai mi­hin Rhe­sus-luok­kaan (Rh + tai Rh -) he kuu­lu­vat. Jo­kai­nen ih­mi­nen kuu­luu yh­teen veri­ryh­mään ja yh­teen Rhe­sus-luok­kaan. Suo­ma­lai­set ovat ja­kau­tu­neet eri veri­ryh­miin ja Rh-luok­kiin seu­raa­vas­ti:

Klik­kaa kaa­vi­o­ta suu­ren­taak­se­si!

Veri­ryh­mä ja Rhe­sus-luok­ka ovat toi­sis­taan riip­pu­mat­to­mia eli veri­ryh­män pe­rus­teel­la ei voi pää­tel­lä kum­paan Rhe­sus-luok­kaan hen­ki­lö kuu­luu.

Mikä on to­den­nä­köi­syys, että sa­tun­nai­ses­ti va­li­tun suo­ma­lai­sen

1. veri­ryh­mä on O?
2. veri­ryh­mä on AB ja Rhe­sus-luok­ka on ne­ga­tii­vi­nen eli hen­ki­lön kuu­luu ryh­miin AB ja Rh- ?

Ratkaisu:

1. (P veri­ryh­mä on O) = 0,3 = 30%
2. P (AB ja Rh- ) = P (AB) ∙ P (Rh-) = 0,08 ∙ 0,16 ≈ 0,013 ≈1,3 %