17. Yleinen kertosääntö
Oikean lottorivin todennäköisyys saadaan lasketuksi kertolaskun avulla. Lottonumerot ovat kuitenkin toisistaan riippuvia tapahtumia. Laskussa on huomioitava, että samoja numeroita ei voida valita uudestaan ja siten seuraavaa numeroa valittaessa ei mahdollisia numeroita olekaan enää yhtä paljon kuin edellisessä vaiheessa.
Yleinen kertosääntö:
Jos tapahtumat A ja B ovat riippuvia, on kertosääntö muotoa
P (ensin A ja B sitten)= P (A) ∙ P (B, kun A on tapahtunut).
Tapahtuman B todennäköisyyttä laskettaessa otetaan siis huomioon, että tapahtuma A on jo sattunut.
Esimerkki 1
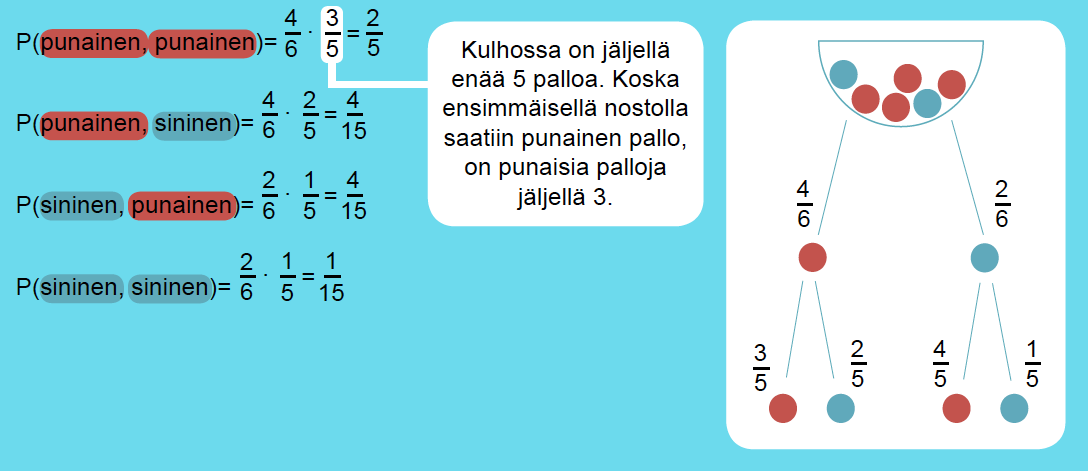
Kulhossa on 4 punaista ja 2 sinistä kuulaa. Kulhosta nostetaan peräkkäin kaksi kuulaa. Tutkitaan, mitkä ovat eri mahdollisuudet ja millä todennäköisyyksillä ne tapahtuvat.
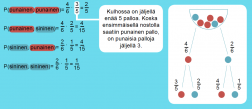
Klikkaa kaaviota suurentaaksesi!
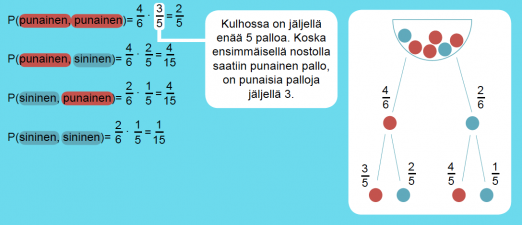
Klikkaa kaaviota suurentaaksesi!
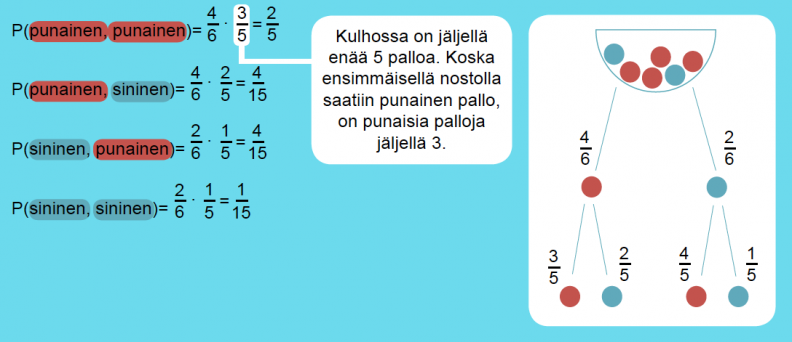
Klikkaa kaaviota suurentaaksesi!
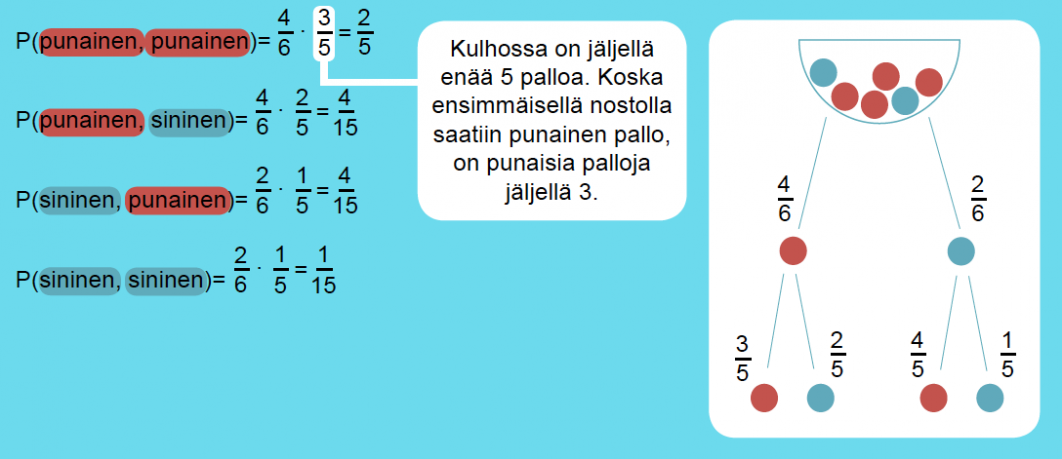
Klikkaa kaaviota suurentaaksesi!
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
Puudiagrammi sisältää kaikki eri mahdollisuudet. Lasketaan vielä tarkistukseksi kaikkien mahdollisuuksien todennäköisyyksien summa.
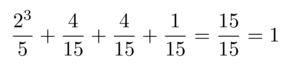
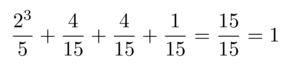
Esimerkki 2
Lasketaan millä todennäköisyydellä lotossa saadaan yhdellä rivillä 7 oikein.
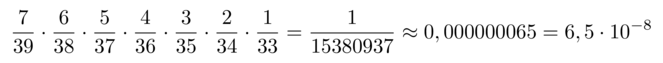
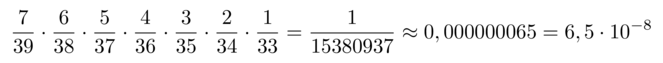
Oletetaan, että yhden rivin täyttämiseen menee 10 sekuntia ja että muistamme aiemmin täyttämämme rivit. Tällöin kaikkien mahdollisten lottorivien tekemiseen kuluu aikaa 153 809 370 sekuntia eli noin 5 vuotta.
Avoin matematiikkaTilastoja ja todennäköisyyksiä4.4.2013