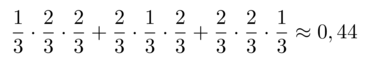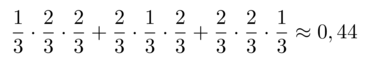18. Erillisten tapahtumien yhteenlaskusääntö

Toi­nen to­den­nä­köi­syys­las­ken­nan pe­rus­las­ku­toi­mi­tuk­sis­ta on yh­teen­las­ku. Yh­teen­las­kun avul­la tar­kas­tel­laan sa­man sa­tun­nais­il­mi­ön eri­lai­sia ta­pah­tu­mis­mah­dol­li­suuk­sia. Täl­lai­nen on esi­mer­kik­si ti­lan­ne, jos­sa ky­sy­tään to­den­nä­köi­syyt­tä saa­da no­pan­hei­tos­sa sil­mä­lu­vuk­si vii­si tai kuu­si. Sa­man­ai­kai­ses­ti ei voi­da saa­da mo­lem­pia, mut­ta näis­tä kel­paa tu­lok­sek­si kum­pi­kin. Yh­teen­las­kun avul­la las­ke­taan to­den­nä­köi­syys sil­le, että kah­des­ta sa­man­ai­kai­ses­ti esiin­ty­mät­tö­mäs­tä ta­pauk­ses­ta jom­pi­kum­pi esiin­tyy. Ta­pah­tu­mia ”saa­daan vii­to­nen” ja ”saa­daan kuu­to­nen” kut­su­taan eril­li­sik­si ta­pah­tu­mik­si.

Esimerkki 1

Las­ke­taan to­den­nä­köi­syys, että yh­del­lä no­pal­la hei­tet­tä­es­sä saa­daan sil­mä­lu­vuk­si vii­to­nen tai kuu­to­nen.

P(vii­to­nen tai kuu­to­nen) = P(vii­to­nen) + P(kuu­to­nen) = 1/6 + 1/6 = 2/6 = 1/3

Esimerkki 2

Nos­te­taan kort­ti­pa­kas­ta yksi kort­ti. Las­ke­taan, mil­lä to­den­nä­köi­syy­del­lä kort­ti on ruu­tu tai hert­ta.

P(ruu­tu tai hert­ta) = P(ruu­tu) + P(hert­ta) = 13/52 + 13/52 = 26/52 = 1/2

Ker­to­las­ku- ja yh­teen­las­ku­sään­tö­jen so­vel­ta­mi­ses­sa on syy­tä olla tark­ka­na. Las­ku­sään­tö­jen käy­tön hah­mot­ta­mi­nen hel­pot­tuu, kun ti­lan­ne kir­joi­te­taan yk­si­tyis­koh­tai­ses­ti pa­pe­ril­le. Ja-sa­nan koh­dal­la on ky­sees­sä ker­to­las­ku. Tai-sa­nan koh­dal­la on ky­sees­sä yh­teen­las­ku.

Esimerkki 3

Kul­hos­ta, jos­sa on 13 pu­nais­ta pal­loa ja 15 si­nis­tä pal­loa, nos­te­taan pe­räk­käin kak­si pal­loa. Mil­lä to­den­nä­köi­syy­del­lä pal­lot ovat eri­vä­ri­set?

Ratkaisu:

Ti­lan­ne to­teu­tuu kun en­sim­mäi­nen pal­lo on pu­nai­nen ja toi­nen si­ni­nen tai en­sim­mäi­nen pal­lo on si­ni­nen ja toi­nen pu­nai­nen.
P(eri­vä­ri­set pal­lot) = P(pu­nai­nen) ∙ P(si­ni­nen) + P(si­ni­nen) ∙ P(pu­nai­nen)

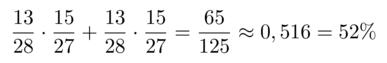
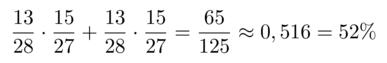
Esimerkki 4

Moni­va­lin­ta­ko­kees­sa on jo­kai­sel­le vas­tauk­sel­le an­net­tu 3 vas­taus­vaih­to­eh­toa, jois­ta yksi on oi­kea. Mikä on to­den­nä­köi­syys, että op­pi­las, joka vas­taa ko­kee­seen ar­vaa­mal­la, saa kol­mes­ta teh­tä­väs­tä oi­kein vain yh­den?

Ratkaisu:

Yksi oi­kea vas­taus saa­daan, jos en­sim­mäi­nen teh­tä­vä on oi­kein ja toi­nen vää­rin ja kol­mas vää­rin. Oi­kea vas­taus voi osua en­sim­mäi­seen tai toi­seen tai kol­man­teen teh­tä­vään.