1. Pulmatehtäviä

Ma­te­maat­ti­sen on­gel­man rat­kai­se­mi­nen aloi­te­taan yleen­sä ra­jaa­mal­la on­gel­mas­ta pois ta­pauk­set, jot­ka ei­vät täy­tä ky­sy­myk­sen eh­to­ja. On­gel­mas­ta py­ri­tään si­ten te­ke­mään pie­nem­pi.

Esimerkki 1

Mil­la on va­lin­nut pu­he­lin­lu­et­te­los­ta hen­ki­lön. Ju­hon tu­lee rat­kais­ta, ke­net Mil­la on va­lin­nut esit­tä­mäl­lä mah­dol­li­sim­man vä­hän ky­sy­myk­siä, joi­hin Mil­la vas­taa joko kyl­lä tai ei.

Ratkaisu

Jos Juho ryh­tyi­si umpi­mäh­kään ar­vai­le­maan hen­ki­löi­tä, hän luul­ta­vas­ti ar­vai­li­si Mil­lan va­lit­se­maa hen­ki­löä vie­lä huo­men­na­kin. On­gel­ma voi­daan kui­ten­kin hel­pos­ti ra­ja­ta.

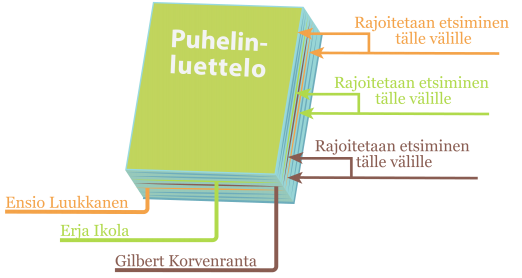
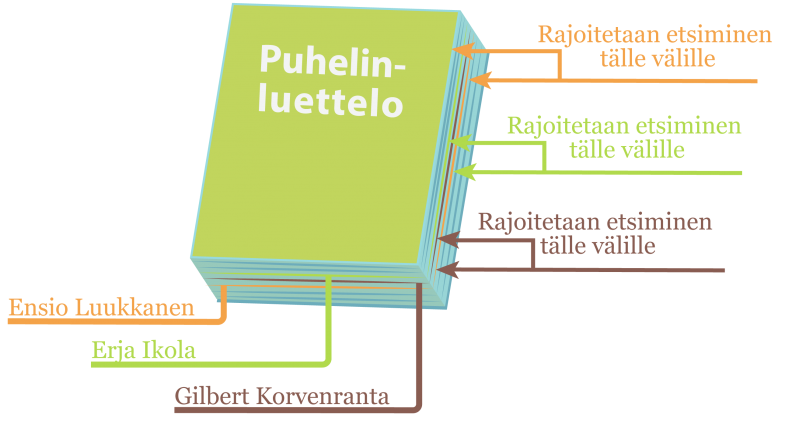
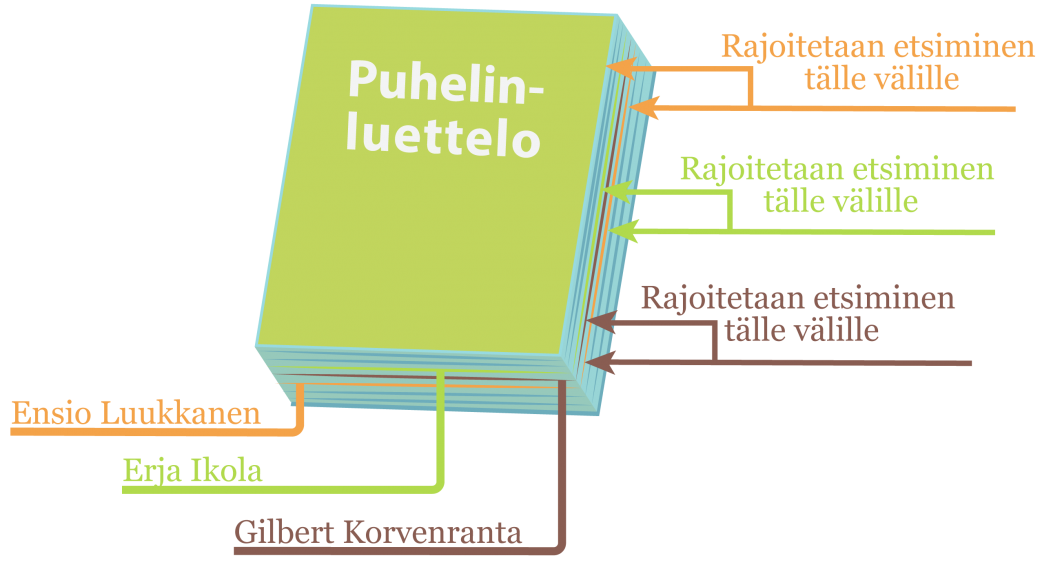
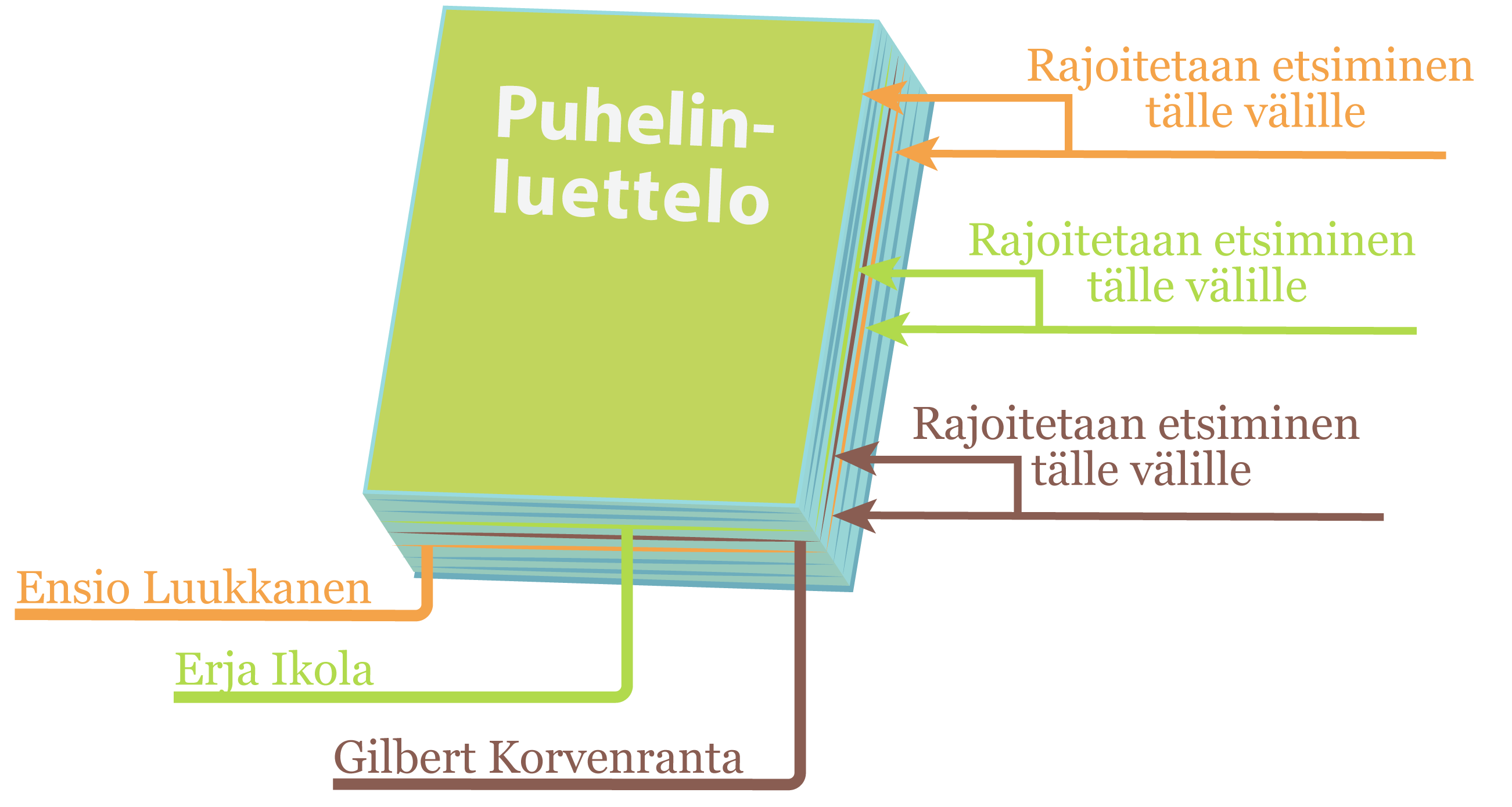
Juho avaa pu­he­lin­lu­et­te­lon puo­li­vä­lis­tä ja saa en­sim­mäi­sen ky­sy­myk­sen­sä avul­la ra­jat­tua kum­mas­sa puo­lis­kos­sa lu­et­te­loa hen­ki­lö esiin­tyy. Seu­raa­val­la ky­sy­myk­sel­lä hän ra­jaa edel­li­sen alu­een taas puo­li­vä­lis­tä jne.

Klik­kaa ku­vaa suu­rem­mak­si!

Avoin ma­te­ma­tiik­ka 7Osio 1: Las­ke­taan re­aa­li­lu­vuil­la20.5.2014