4. Itseisarvo ja vastaluku
Lukusuoralla luvun etäisyyttä nollasta kutsutaan luvun itseisarvoksi.
Luvun a itseisarvoa merkitään |a|.
Kun halutaan tietää kuinka kaukana luku on nollasta, välittämättä siitä kummalla puolella nollaa se on, merkitään pystyviivat luvun molemmille puolille. Koska itseisarvo kuvaa etäisyyttä, se ei voi olla koskaan negatiivinen.
Esimerkki 1.
a) |3| = 3
Positiivisen luvun itseisarvo on luku itse.
b) |0| = 0
Nollan itseisarvo on nolla.
c) Negatiivisen luvun itseisarvo on vastaava luku ilman etumerkkiä.
Lukujen itseisarvot lasketaan ennen muita laskutoimituksia. Jos itseisarvomerkkien sisällä on lauseke, on sen arvo laskettava ennen itseisarvomerkkien poistamista.
Esimerkki 2.
a) |-16| + | -8| = 16 + 8 = 24
Otetaan ensin lukujen itseisarvot ja lasketaan ne yhteen.
b) |32 – 10 + 4| = |26| = 26
Lasketaan ensin luvut yhteen ja otetaan summan itseisarvo.
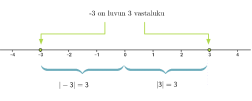
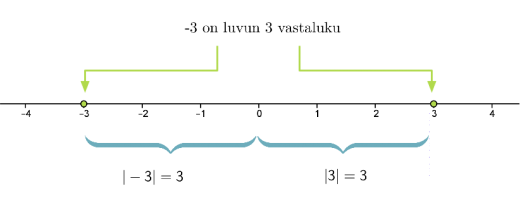
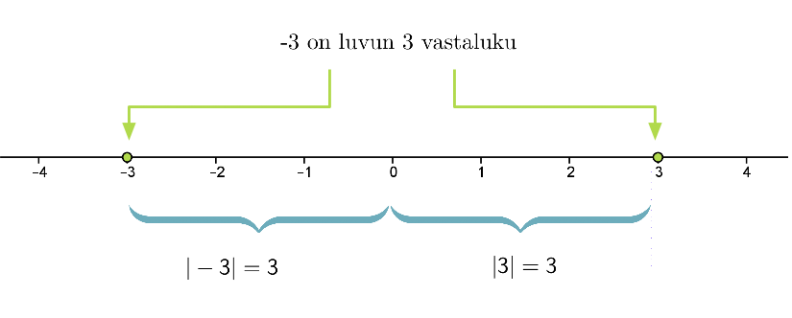
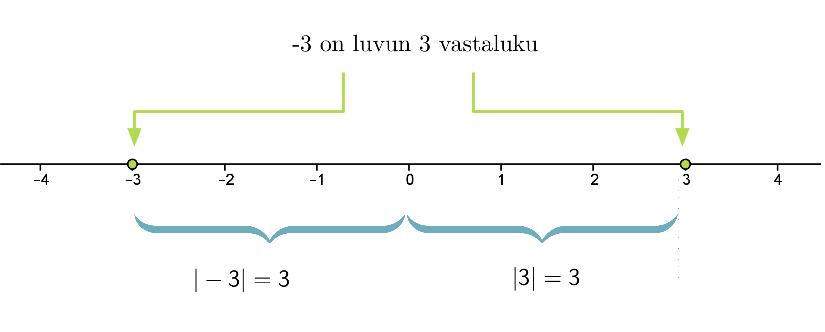
Kahta lukua, jotka sijaitsevat lukusuoralla yhtä kaukana nollasta, mutta sen eri puolilla, sanotaan toistensa vastaluvuiksi.
Esimerkki 3.
Klikkaa kaavota suuremmaksi!
Klikkaa kaavota suuremmaksi!
Klikkaa kaavota suuremmaksi!
Klikkaa kaavota suuremmaksi!

Klikkaa kaavota suuremmaksi!
Vastaluvuilla on sama itseisarvo. Positiivisen luvun vastaluku saadaan laittamalla miinusmerkki luvun eteen. Negatiivisen luvun vastaluku saadaan jättämällä miinusmerkki pois luvun edestä.
Esimerkki 4.

Luvut ja vastaluvut

Luvut ja vastaluvut
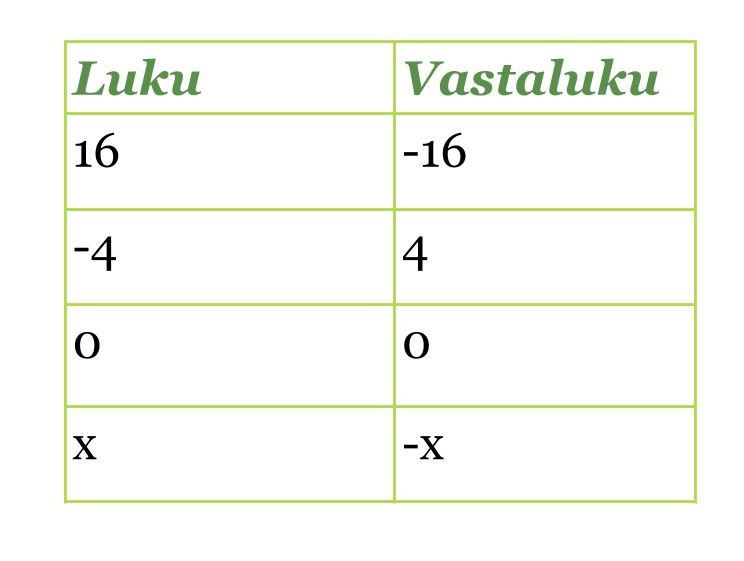
Luvut ja vastaluvut

Luvut ja vastaluvut
Matemaattisesti vastaluku merkitään laittamalla luvun eteen miinusmerkki. Jos luvun edessä on ennestään plus- tai miinusmerkki, on luku laitettava sulkeisiin. Kahta laskutoimitusmerkkiä ei voi esiintyä peräkkäin ilman, että välissä olisi sulkeet. Peräkkäisillä laskutoimitusmerkeillä laskeminen opitaan myöhemmin.
Esimerkki 5.
a) Luvun 9 vastaluku merkitään −9.
b) Luvun +9 vastaluku merkitään −(+9).
c) Luvun – 9 vastaluku merkitään −(−9).
Avoin matematiikka 7Osio 1: Lasketaan reaaliluvuilla20.5.2014