6. Merkkiyhdistelmien sieventäminen
Lukusuoralla tarkastelun lisäksi vastalukuja voidaan tarkastella laskemalla ne yhteen.
Kahta lukua, joiden summa on nolla, sanotaan toistensa vastaluvuiksi eli luvun a vastaluku on –a, koska
a + (-a) = 0.
Luvun -8 vastaluku on -(-8), mutta miten voidaan osoittaa, että -8+[-(-8)] = 0, kun laskutoimituksessa on peräkkäisiä plus- ja miinusmerkkejä?
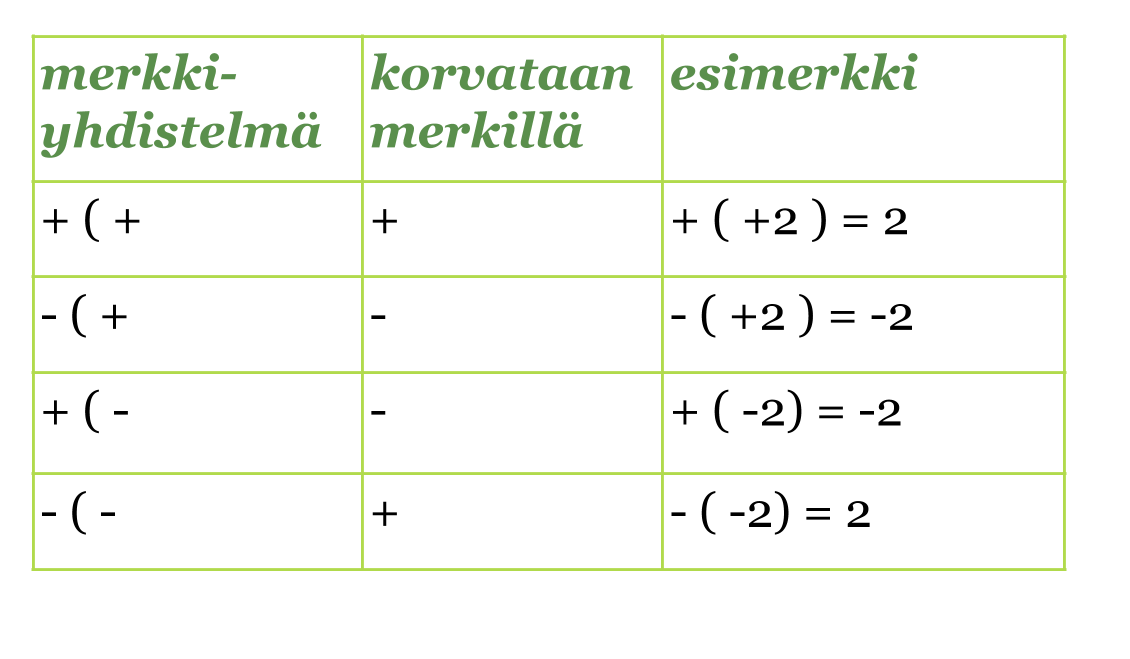
Kahden etu- ja laskumerkin yhdistelmät, joissa merkkien välissä on sulkumerkki, voidaan korvata yhdellä merkillä. Jos sulkeiden edessä on plusmerkki, ei sulkeiden sisällä olevien etumerkkejä muuteta. Jos sulkeiden edessä on miinusmerkki, kaikkien sulkeiden sisällä olevien lukujen etumerkki vaihdetaan.
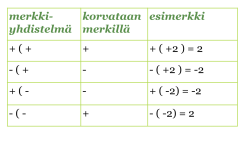
Klikkaa taulukko suuremmaksi!
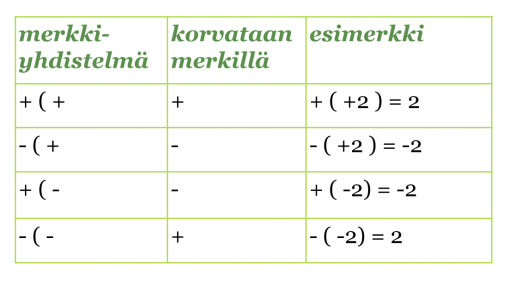
Klikkaa taulukko suuremmaksi!
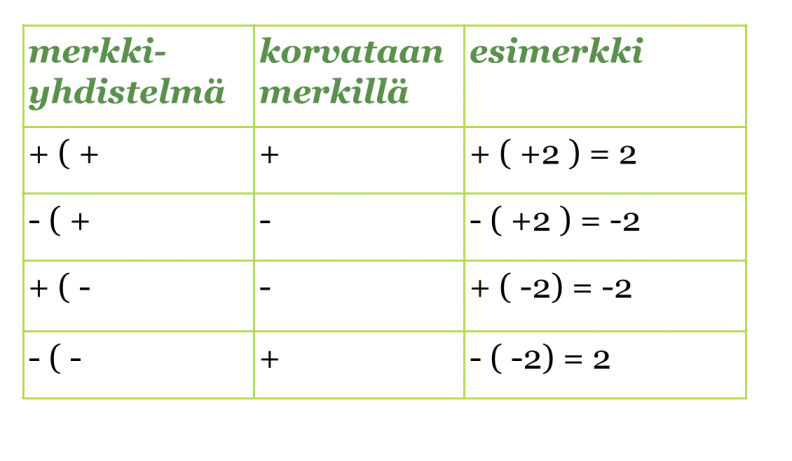
Klikkaa taulukko suuremmaksi!
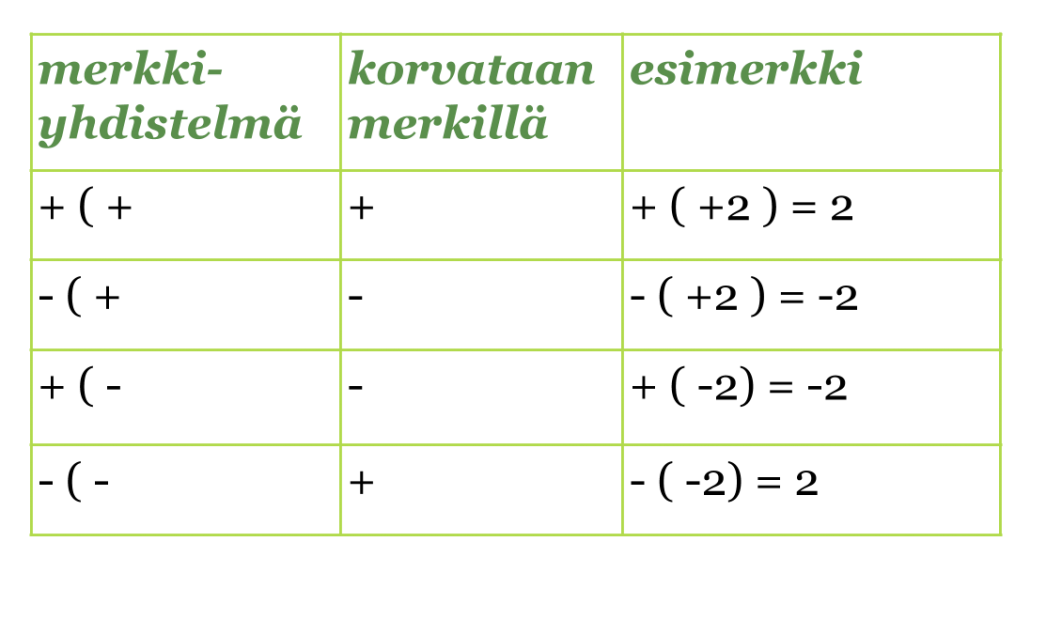
Klikkaa taulukko suuremmaksi!
Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!
Miinusmerkkiä voisi verrata kieltävään sanaan ”ei”. Kaksi peräkkäin olevaa ei -sanaa kumoavat toisensa. Esimerkiksi ”ei pidä paikkaansa etten ole terve” tarkoittaa samaa kuin ”olen terve”.
Koska sulkeiden edessä oleva + -merkki ei muuta sulkeiden sisällä olevien etumerkkiä, voidaan kaikki yhteen ja vähennyslaskut ajatella positiivisten ja negatiivisten lukujen yhteenlaskuina. Esimerkiksi lauseke – 8 – 4 voidaan kirjoittaa muodossa ( – 8) + ( – 4).
Esimerkki 1.
Poistetaan sulkeet ja suoritetaan laskutoimitukset.
- 5 + (+ 3) = 5 + 3 = 8
- 5 – (+ 3) = 5 – 3 = 2
- 5 + (-3) = 5 – 3 = 2
- 5 – (-3) = 5 + 3 = 8
Esimerkki 2.
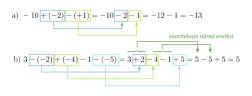
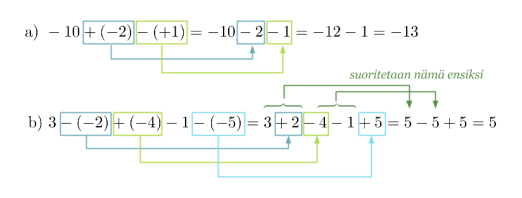
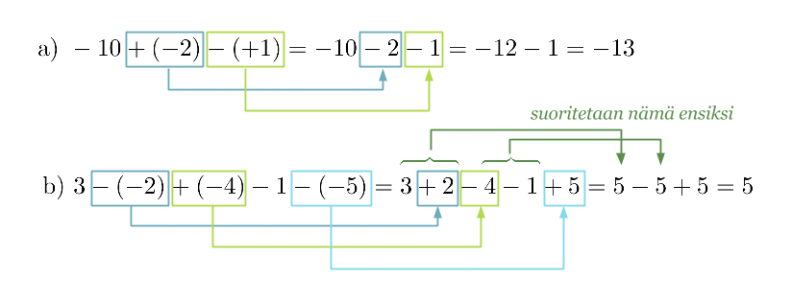
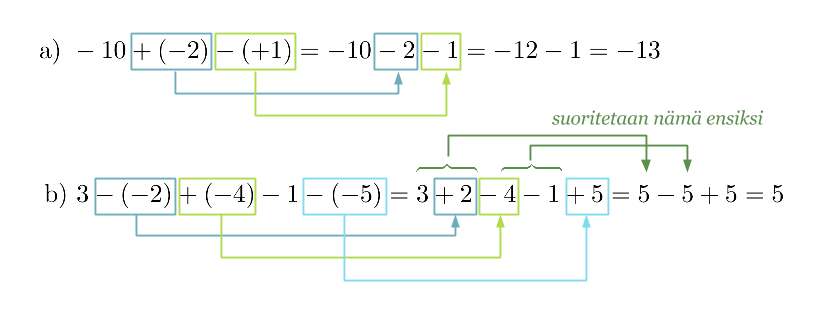
Poistetaan sulkeet ja suoritetaan laskutoimitukset.
Klikkaa kaaviota suuremmaksi!
Klikkaa kaaviota suuremmaksi!
Klikkaa kaaviota suuremmaksi!
Klikkaa kaaviota suuremmaksi!

Klikkaa kaaviota suuremmaksi!