9. Monikerrat ja jaollisuus
Luvun monikerta saadaan, kun luku kerotaan luonnollisella luvulla. Monikerroista muodostuu kyseisen luvun kertotaulu.
Esimerkki 1.
a) Luvun 2 monikertoja ovat 2, 4, 6, 8, 10, 12, … kaikki nämä luvut ovat jaollisia luvulla 2.
b) Luvun 5 monikertoja ovat 5, 10, 15, 20, 25, … kaikki nämä luvut ovat jaollisia luvulla 5.
Luku on jaollinen toisella luvulla, jos lukujen jakolasku menee tasan eli tulos on kokonaisluku. Jos luku ei ole jaollinen toisella luvulla, jakolaskusta jää jakojäännös.
Luvulla jaollisia ovat vain kyseisen luvun monikerrat. Joka toinen kokonaisluku on jaollinen kahdella. Joka kolmas kokonaisluku on jaollinen kolmella jne.
Esimerkki 2.
a) 1024 on jaollinen kahdella, koska viimeinen numero on 4.
b) 12345 on jaollinen kolmella, koska
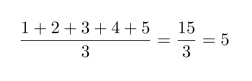
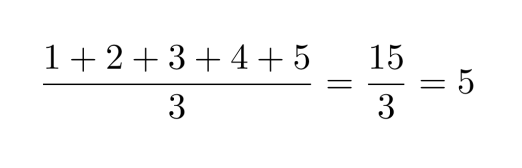
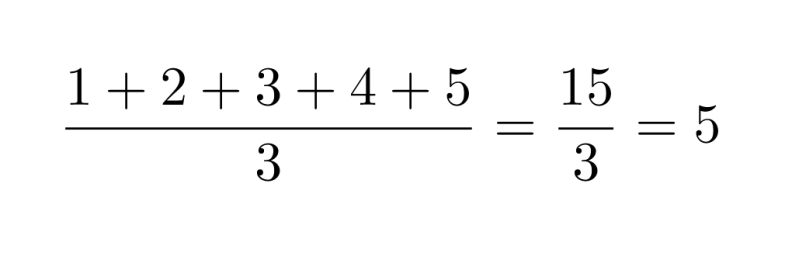


c) 6725 on jaollinen viidellä, koska sen viimeinen numero on 5.
d) 246 on jaollinen kuudella, koska sen viimeinen numero on 6 ja
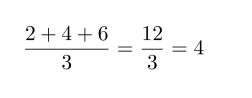
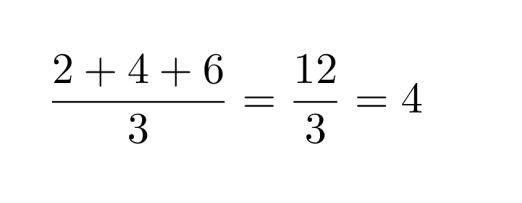
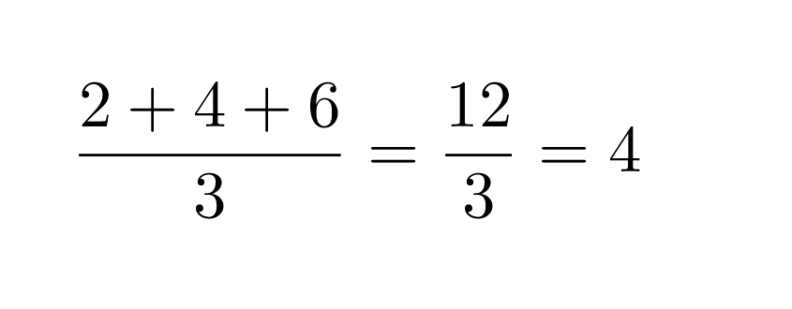
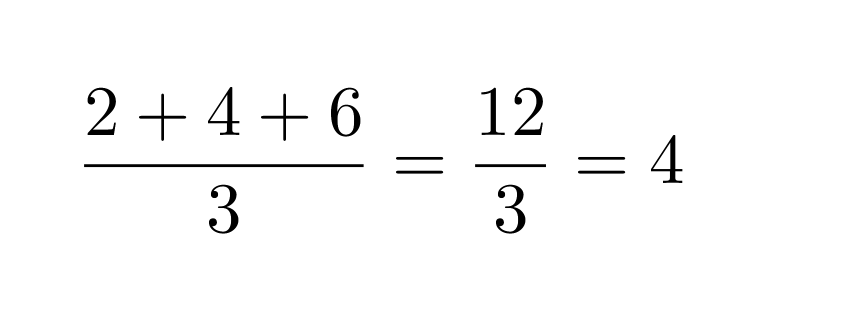

e) 3456 on jaollinen yhdeksällä, koska
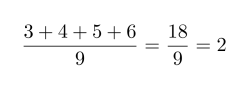
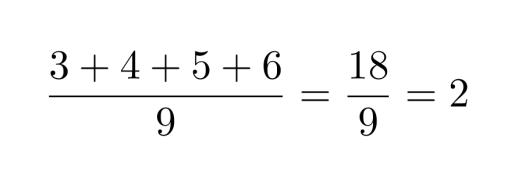
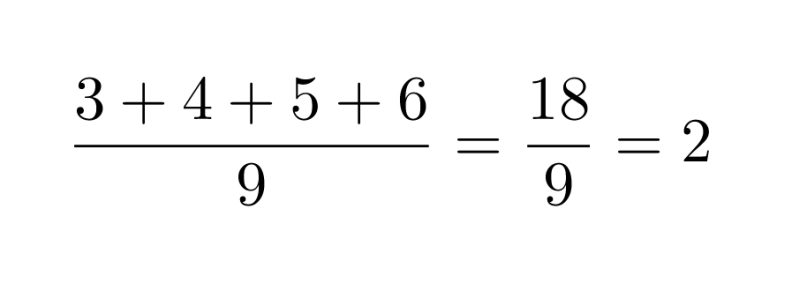
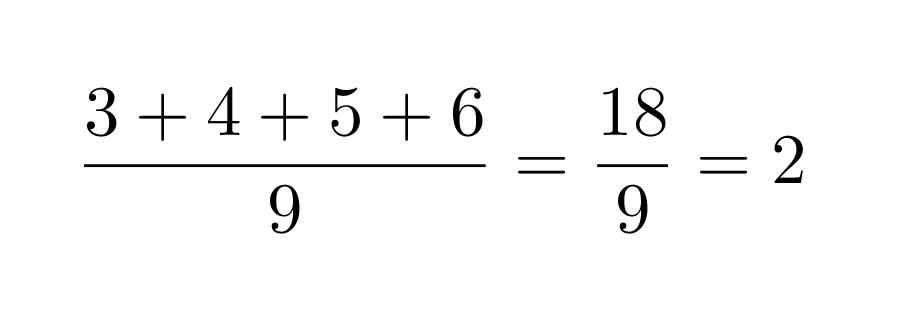

f) 2479120 on jaollinen kymmenellä, koska viimeinen numero on 0.
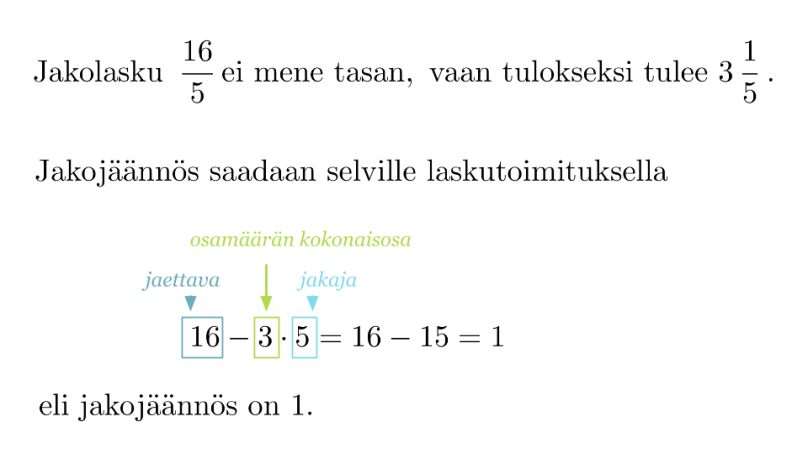
Esimerkki 3.

Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
Klikkaa kaaviota suurentaaksesi!
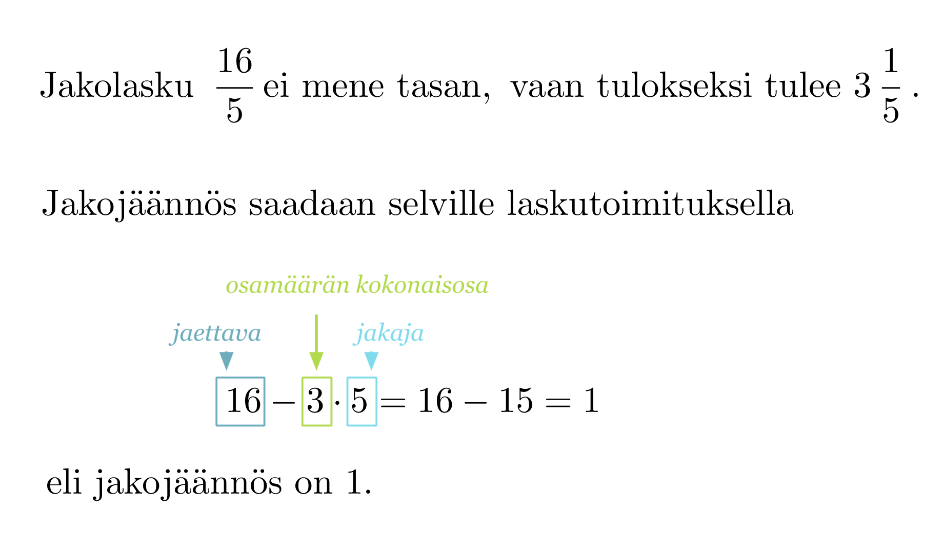
Klikkaa kaaviota suurentaaksesi!

Klikkaa kaaviota suurentaaksesi!
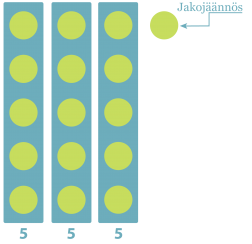
Jakojäännös (16/3), jakojäännös on 1.
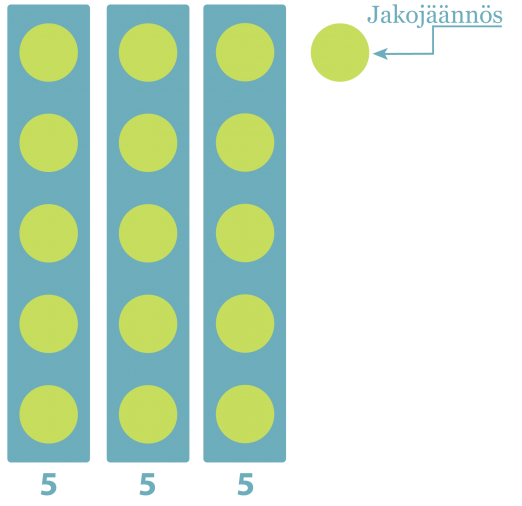
Jakojäännös (16/3), jakojäännös on 1.
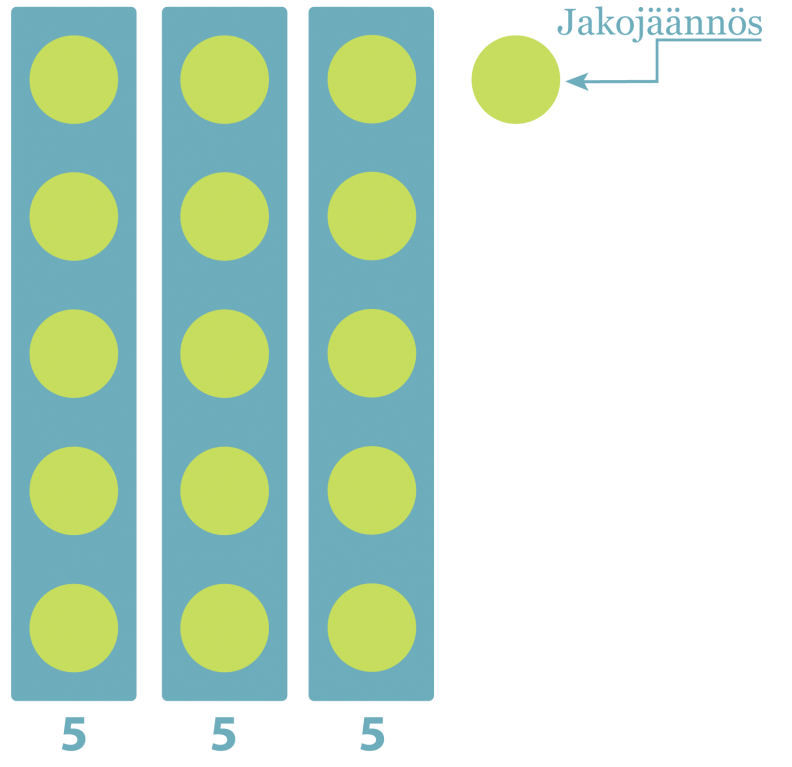
Jakojäännös (16/3), jakojäännös on 1.
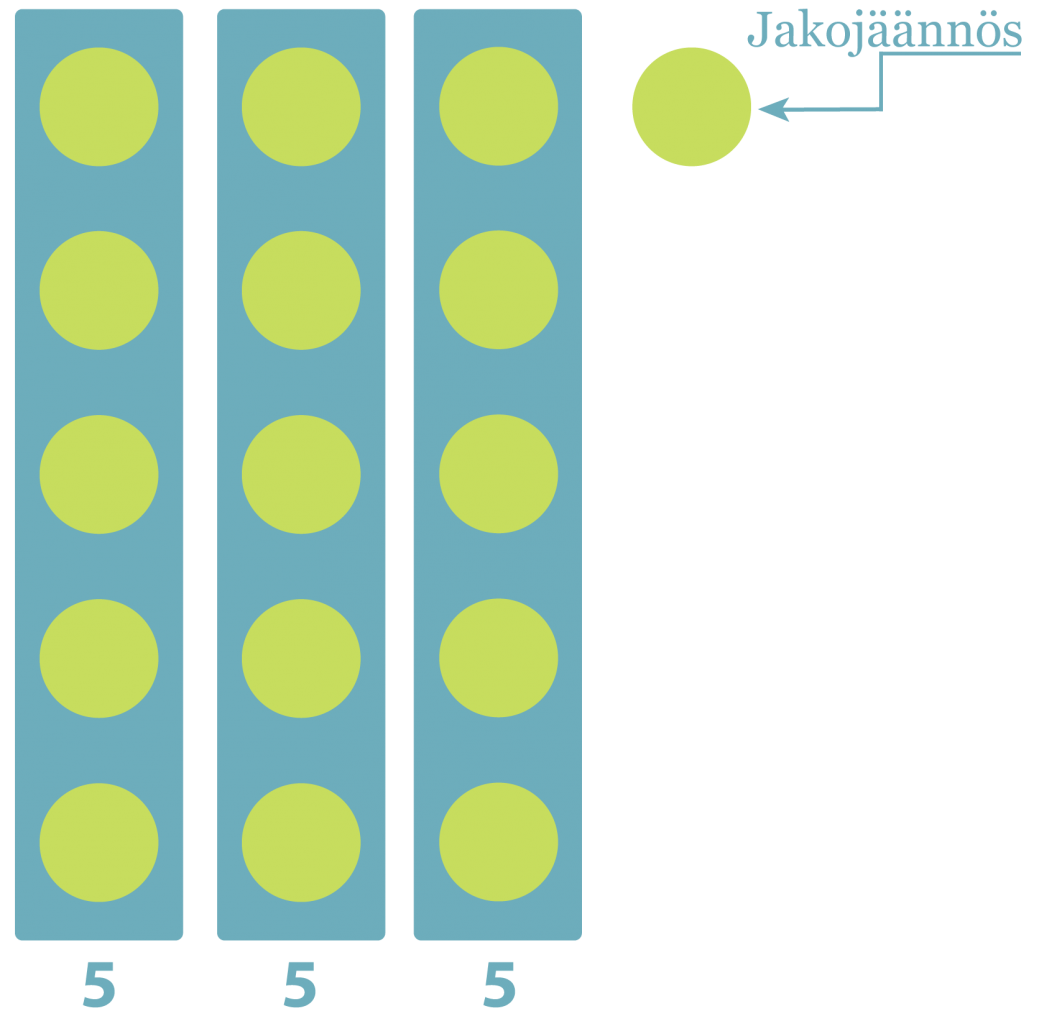
Jakojäännös (16/3), jakojäännös on 1.
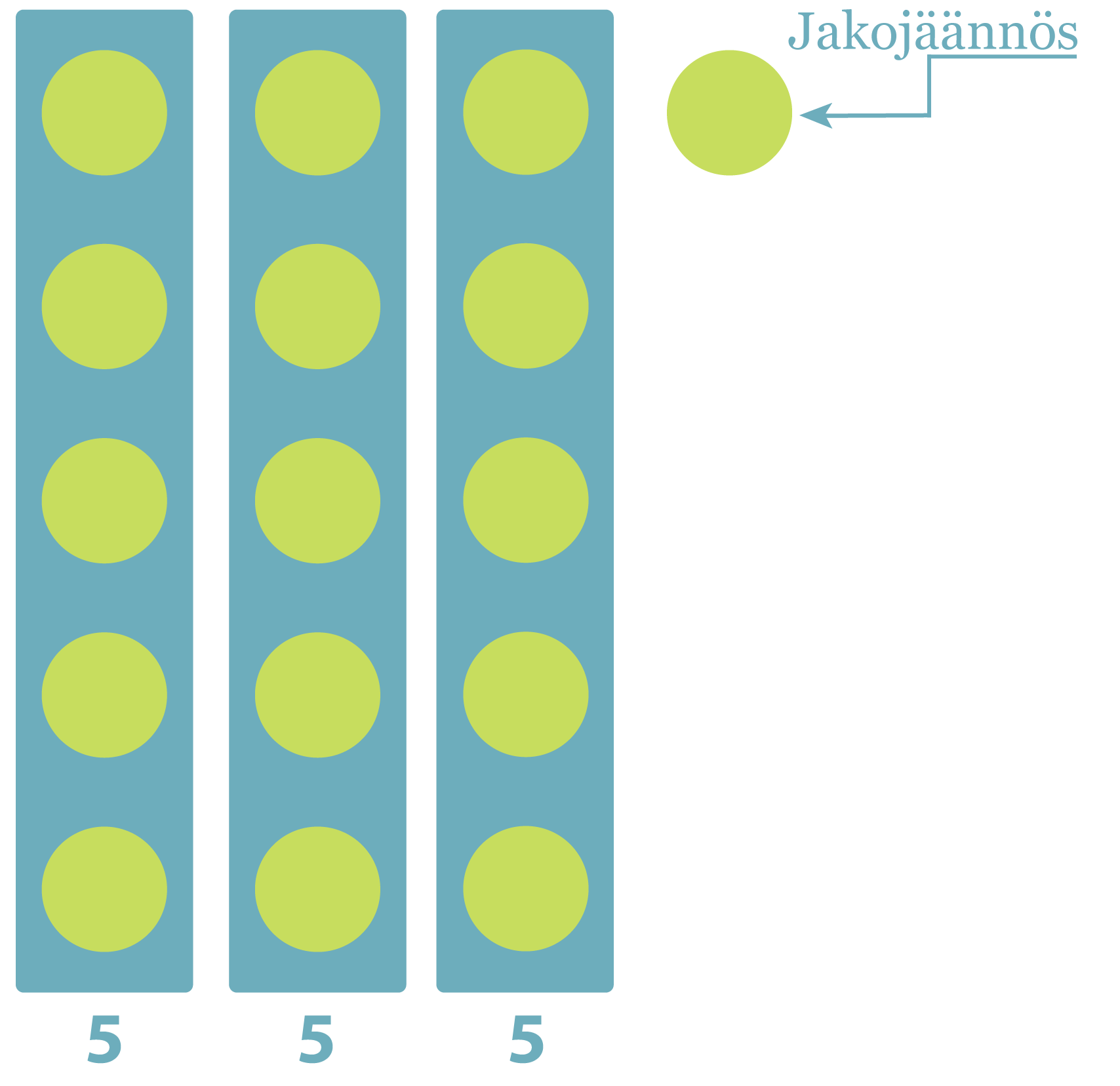
Jakojäännös (16/3), jakojäännös on 1.

Jakojäännös (16/3), jakojäännös on 1.
Lukujen jaollisuussääntöjä
Jokainen luku on jaollinen luvulla yksi ja itsellään. Lisäksi luku on jaollinen