10. Luvun jakaminen tekijöihin
Esimerkki 1.
Lelulaatikossa on 20 pikkuautoa. Tutkitaan monelleko lapselle autot voidaan jakaa tasan.
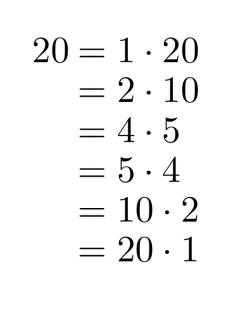
Klikkaa kuva suuremmaksi!
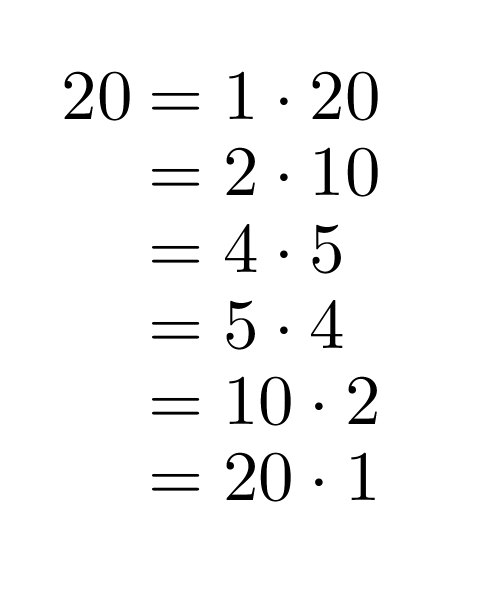
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
- Jos lapsia on vain yksi, hän saa
20 autoa. - Jos lapsia on kaksi, molemmat saavat 10 autoa.
- Jos lapsia on neljä, kukin saa
5 autoa jne.
Pikkuautot menevät tasan, jos lapsia on 1, 2, 4, 5, 10 tai 20. Luku 20 on siis näillä kaikilla jaollinen. Lukuja 1, 2, 4, 5, 10 ja 20 sanotaan luvun 20 tekijöiksi.
Luvun tekijöitä ovat luvut, joilla kyseinen luku on jaollinen. Kun luku esitetään tulona, sanotaan sen olevan jaettu tekijöihin.
Esimerkki 2.
a) Etsitään luvun 6 tekijät.
6 = 1 · 6 = 2 · 3
Luvun 6 tekijät ovat 1, 2, 3, 6
b) Etsitään luvun 18 tekijät.
18 = 1 · 18 = 2 · 9 = 3 · 6
Luvun 18 tekijät ovat 1, 2, 3, 6, 9
c) Lukujen 6 ja 18 yht. tekijät ovat 1, 2, 3, 6
Tekijöihin jakoa voidaan jatkaa aina alkutekijöihin asti, jolloin luku esitetään alkulukujen tulona. Alkuluku on siitä erikoinen luku, ettei sitä voi enää jakaa tekijöihin ja jokainen kokonaisluku (≥ 2) voidaan esittää ainoastaan yhdellä tavalla alkulukujen tulona.
Alkuluku on lukua 1 suurempi luonnollinen luku, joka on jaollinen ainoastaan luvulla 1 ja itsellään. Kymmenen ensimmäista alkulukua ovat: 2, 3, 5, 7, 11, 13,17, 19, 22 ja 23.
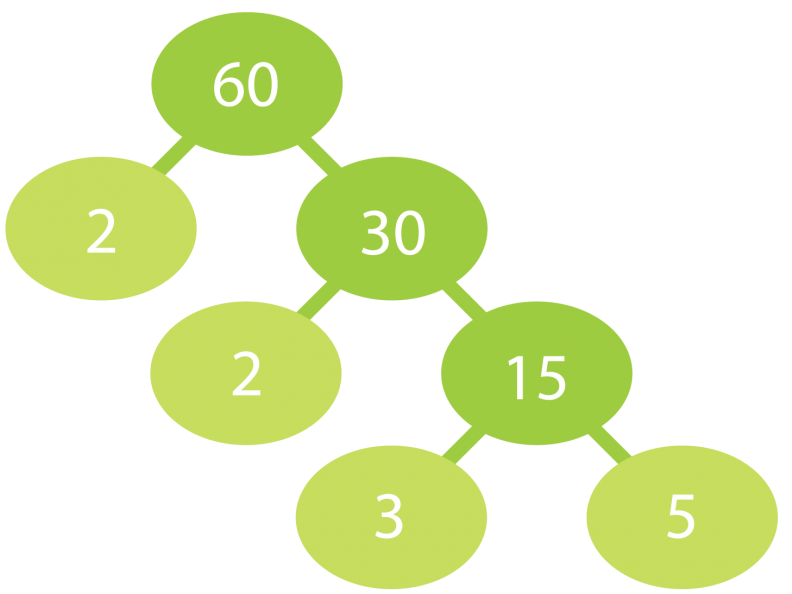
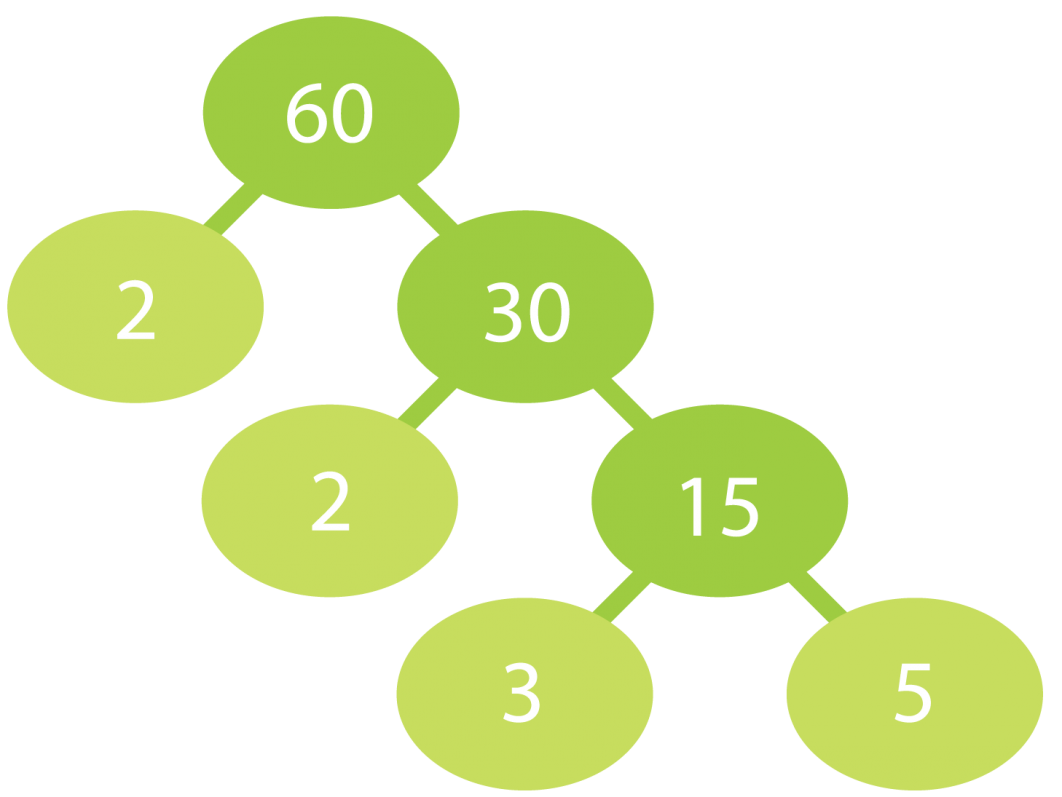
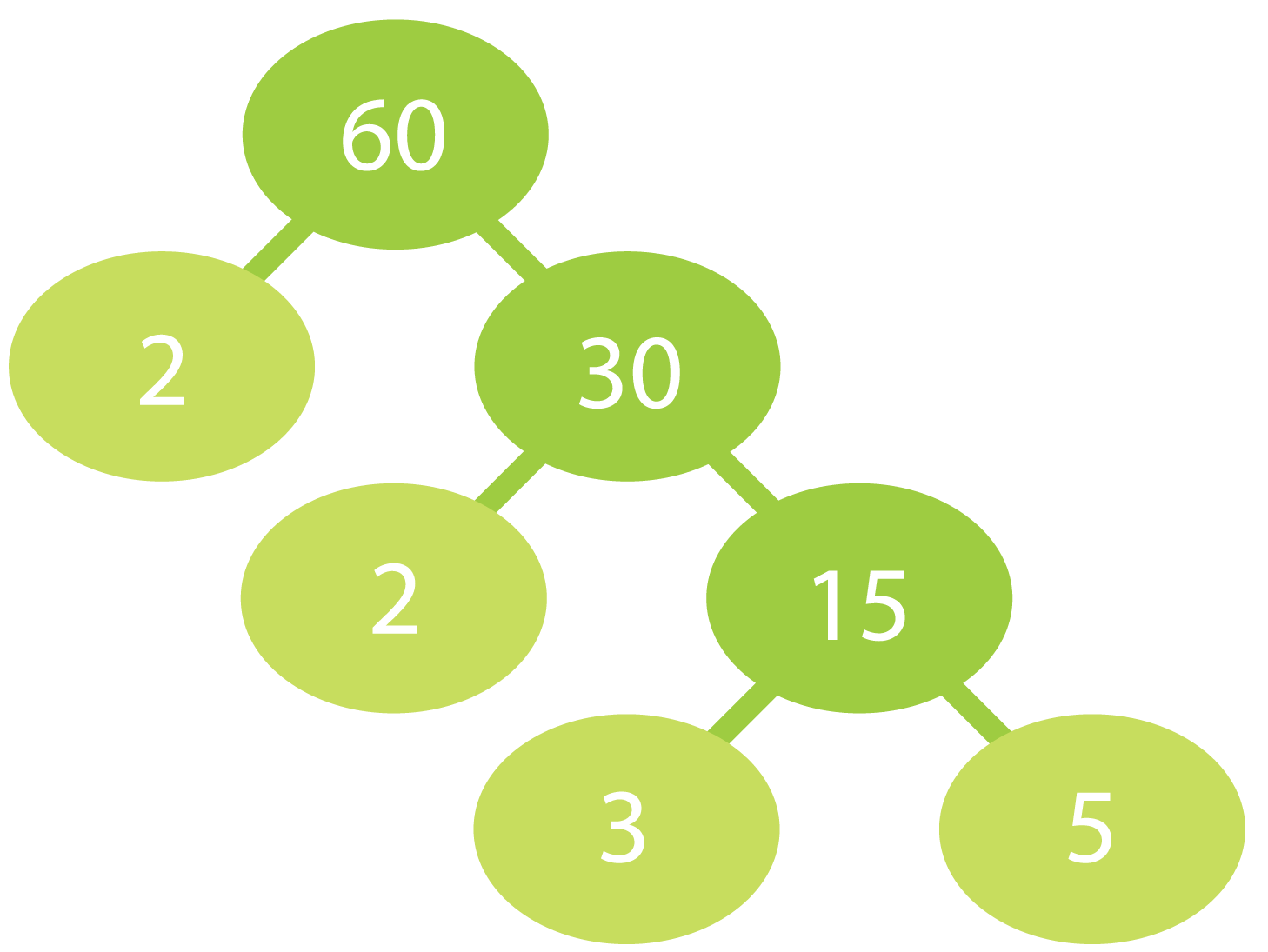
Alkutekijäpuu on oiva apu lukujen jakamisessa alkutekijöihin. Tekijöiksi valitaan aina pienin mahdollinen alkuluku niin kauan kunnes kaikki oksat päättyvät alkulukuihin.
Esimerkki 3.
a) Jaetaan luku 60 alkutekijöihin.
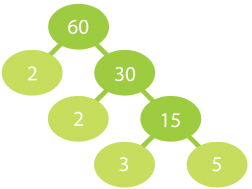
Klikkaa kuvio suuremmaksi!
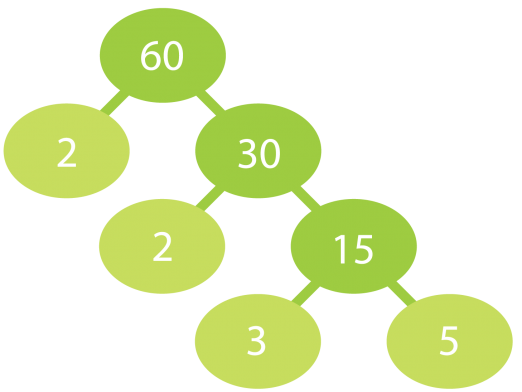
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!

Klikkaa kuvio suuremmaksi!
Luku 60 hajoaa alkutekijöihin seuraavasti:
60 = 2 · 2 · 3 · 5 = 22 · 3 · 5
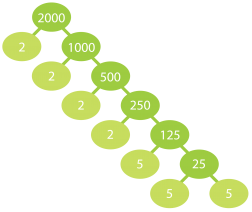
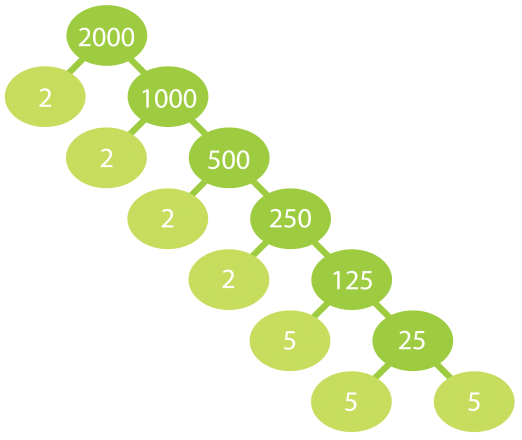
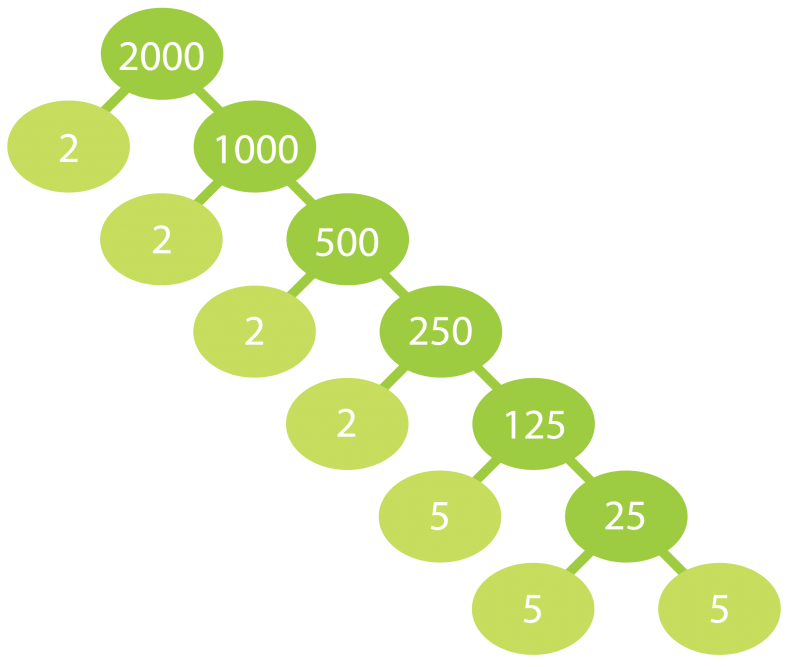
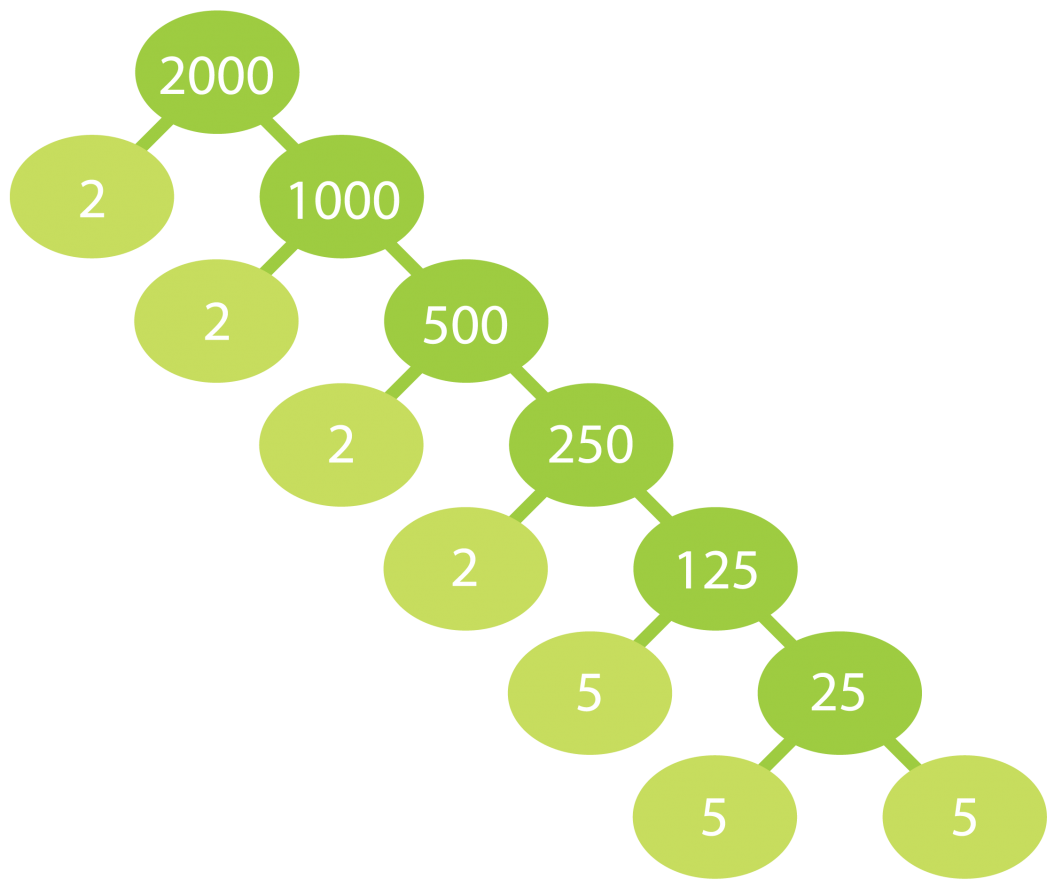
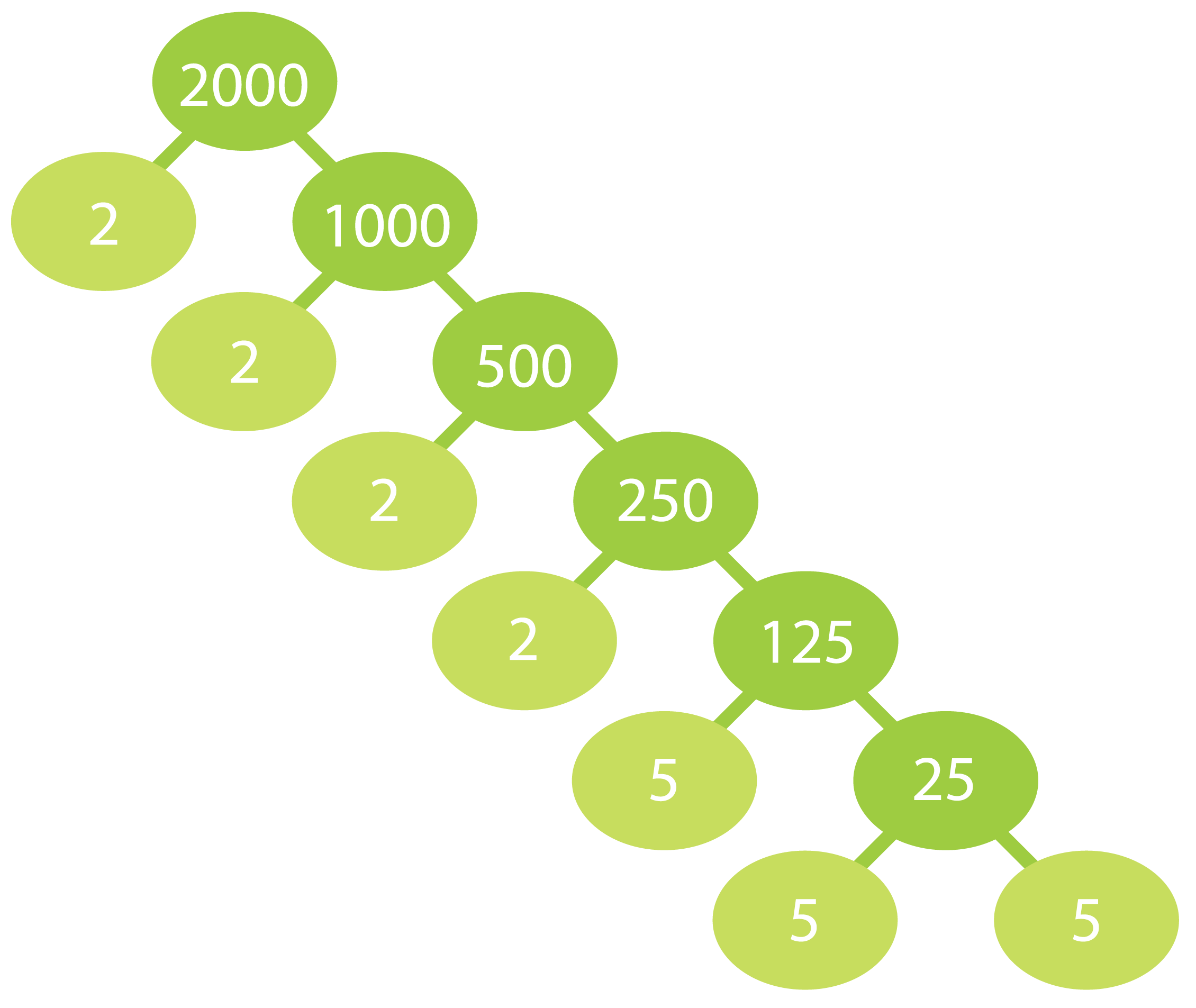
a) Jaetaan luku 2000 alkutekijöihin.
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!
Klikkaa kuvio suuremmaksi!

Klikkaa kuvio suuremmaksi!
Luku 2000 hajoaa alkutekijöihin
seuraavasti:
2000 = 2 · 2 · 2 · 2 · 5 · 5 · 5 = 24 · 53
Avoin matematiikka 7Osio 1: Lasketaan reaaliluvuilla20.5.2014