16. Desimaaliluvut ja merkitsevät numerot
Käyttämämme lukujen merkintäjärjestelmä on nimeltään paikkajärjestelmä, jossa numeron merkitykseen vaikuttaa sen paikka. ”Olet nolla” on ikävästi sanottu, mutta jos nolla sijoitetaan ykkösen jälkeen, tämän arvo kymmenkertaistuu. Paikkajärjestelmiä on olemassa useita erilaisia ja jokaisessa paikkajärjestelmässä on tietty kantaluku. Käyttämämme järjestelmä on desimaalinen, sen kantaluku on 10.
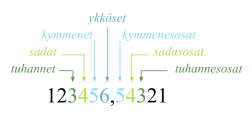




Esimerkki 1.
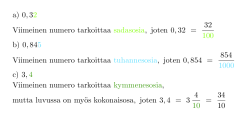
Esitetään murtolukuna a) 0,32 b) 0,845 c) 3,4.
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Desimaaliluvuilla laskettaessa on kiinnitettävä huomiota tulosten oikeaan tarkkuuteen. Laskimella laskettaessa voimme saada lukuja, joiden paikalla voisi olla mitä tahansa lukuja. Kaikkien saatujen lukujen arvoihin ei voi luottaa. Merkitsevät numerot ilmoittavat mitkä luvun numeroista ovat vielä oikeita ja mitkä puppua.
Luvun merkitseviksi numeroiksi katsotaan kaikki muut paitsi desimaaliluvun alussa ja kokonaisluvun lopussa olevat nollat. Joissakin tapauksissa kokonaisluvun lopussakin olevat nollat voivat olla merkitseviä, mikä ilmenee asiayhteydestä.
Esimerkki 2.
- Kokonaisluvussa 500 000 on
yksi merkitsevä numero. - Desimaaliluvussa 0,250 on
kolme merkitsevää numeroa. - Desimaaliluvussa 0,04 on
yksi merkitsevä numero. - Desimaaliluvussa 89,20 on
neljä merkitsevää numeroa. - Kokonaisluvussa 4005 on
neljä merkitsevää numeroa. - Kokonaisluvussa 540 on kaksi tai kolme merkitsevää numeroa riippuen siitä, onko luku pyöristetty.
Kun desimaaliluku katkaistaan, viimeinen mukaan tuleva numero korotetaan yhdellä, jos ensimmäinen pois jäävä numero on 5, 6, 7, 8 tai 9. Desimaalilukuja pyöristettäessä jätetään katkaisukohdan jälkeiset desimaalit pois. Kokonaislukuja pyöristettäessä korvataan katkaisukohdan jälkeiset numerot nollilla.
Esimerkki 3.
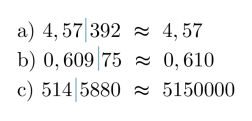
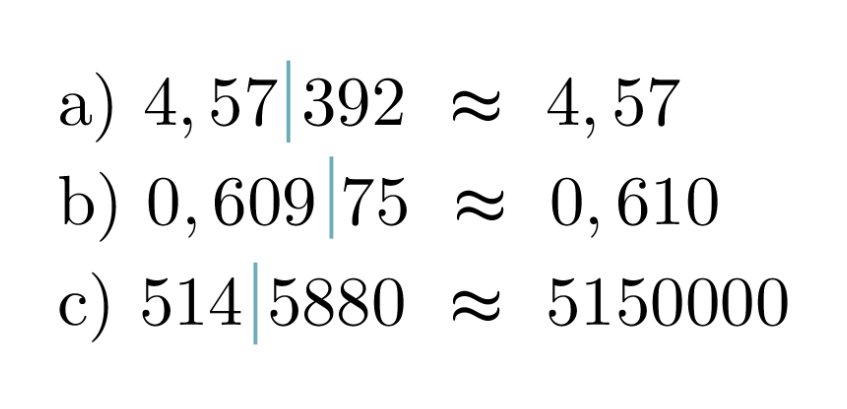
Pyöristetään luvut annetulta kohdalta.
Klikkaa kaaviota suuremmaksi!
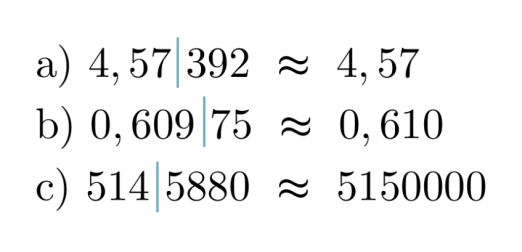
Klikkaa kaaviota suuremmaksi!
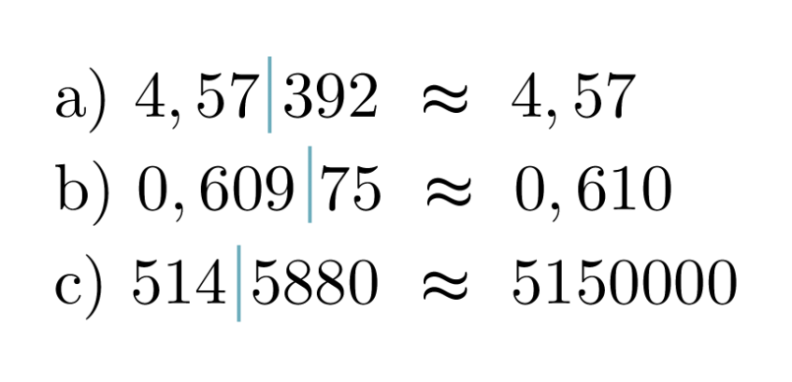
Klikkaa kaaviota suuremmaksi!
Klikkaa kaaviota suuremmaksi!

Klikkaa kaaviota suuremmaksi!
Merkintä ≈ luetaan ”likimäärin yhtä suuri kuin”.
Avoin matematiikka 7Osio 1: Lasketaan reaaliluvuilla20.5.2014