17. Lasketaan desimaaliluvuilla, pyöristyssäännöt

Kun las­ke­taan desi­maa­li­lu­vuil­la, on tu­los­ten tark­kuu­teen kiin­ni­tet­tä­vä eri­tyis­tä huo­mi­o­ta. Muu­toin saa­te­taan va­hin­gos­sa väit­tää teh­ty­jä mit­tauk­sia to­del­li­suut­ta tar­kem­mik­si. Desi­maa­li­lu­vuil­la las­ket­ta­es­sa vas­tauk­set pyö­ris­te­tään so­pi­vaan tark­kuu­teen tiet­ty­jen sään­tö­jen mu­kai­ses­ti.

Esimerkki 1.

Juho ajaa työ­mat­kal­laan 5 km ko­to­aan työ­pai­kan park­ki­pai­kal­le. Park­ki­pai­kal­ta on työ­pai­kan ovel­le 60 m ja ovel­ta 15 m Ju­hon työ­huo­nee­seen. Kuin­ka pit­kä Ju­hon työ­mat­ka on ko­ko­nai­suu­des­saan?

Ratkaisu

5 km + 0,060 km + 0,015 km = 5,075 km

Tar­kas­tel­laan vas­tauk­sen mie­lek­kyyt­tä. Auto­mat­ka on il­moi­tet­tu ko­ko­nais­ten kilo­met­rien tark­kuu­del­la. Sen to­del­li­nen arvo on vä­lil­lä 4,5 km – 5,5 km, jol­loin koko mat­kan pi­tuus tu­li­si ole­maan vä­lil­lä 4,575 km – 5,575 km. Jos nyt Ju­hon työ­mat­kan pi­tuu­dek­si il­moi­te­taan 5,075 km, tar­koit­taa se, että mat­kan pi­tuus on tar­kas­ti 5 km ja 75 m. Saa­dun tu­lok­sen kaik­ki de­si­maa­lit 0, 7 ja 5 voi­vat kui­ten­kin olla mitä ta­han­sa nu­me­roi­ta, kos­ka 5 km mat­kaa ei oltu mi­tat­tu met­rien tark­kuu­del­la. Ai­noa jär­ke­vä vas­taus työ­mat­kan pi­tuu­dek­si, jos­sa voi­daan luot­taa nu­me­roi­den paik­kan­sa­pi­tä­vyy­teen, on 5 km.

Esimerkki 2.

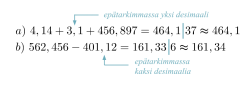
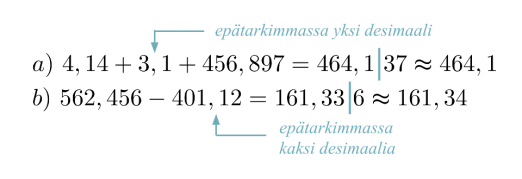
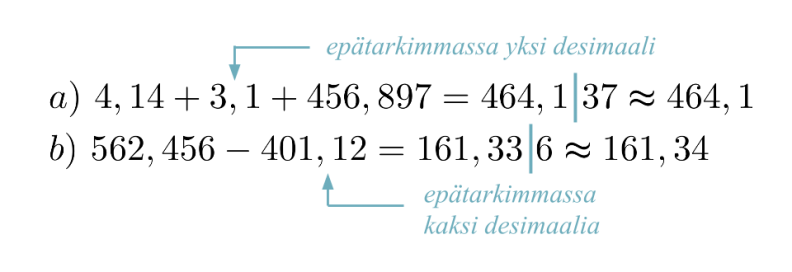
Suo­ri­te­taan las­kut ja an­ne­taan vas­tauk­set so­pi­val­la tark­kuu­del­la.

Klik­kaa kuva suu­rem­mak­si!

Esimerkki 3.

Suo­ri­te­taan las­kut ja an­ne­taan vas­tauk­set so­pi­val­la tark­kuu­del­la.

Klik­kaa kuva suu­rem­mak­si!