1. Harpin käytön kertausta
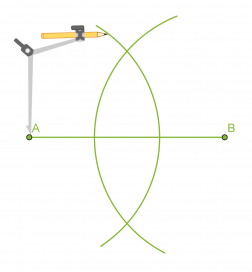
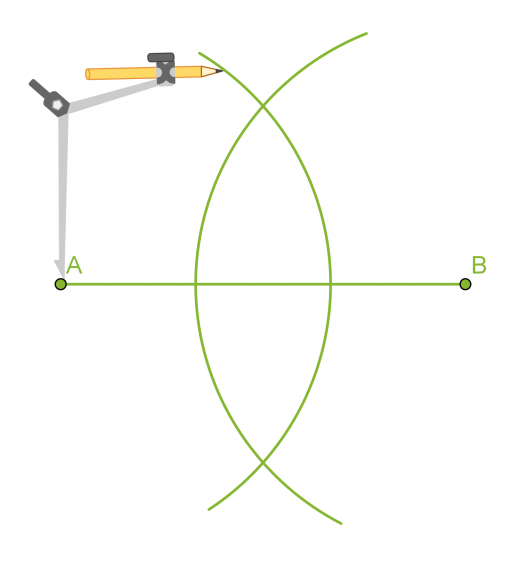
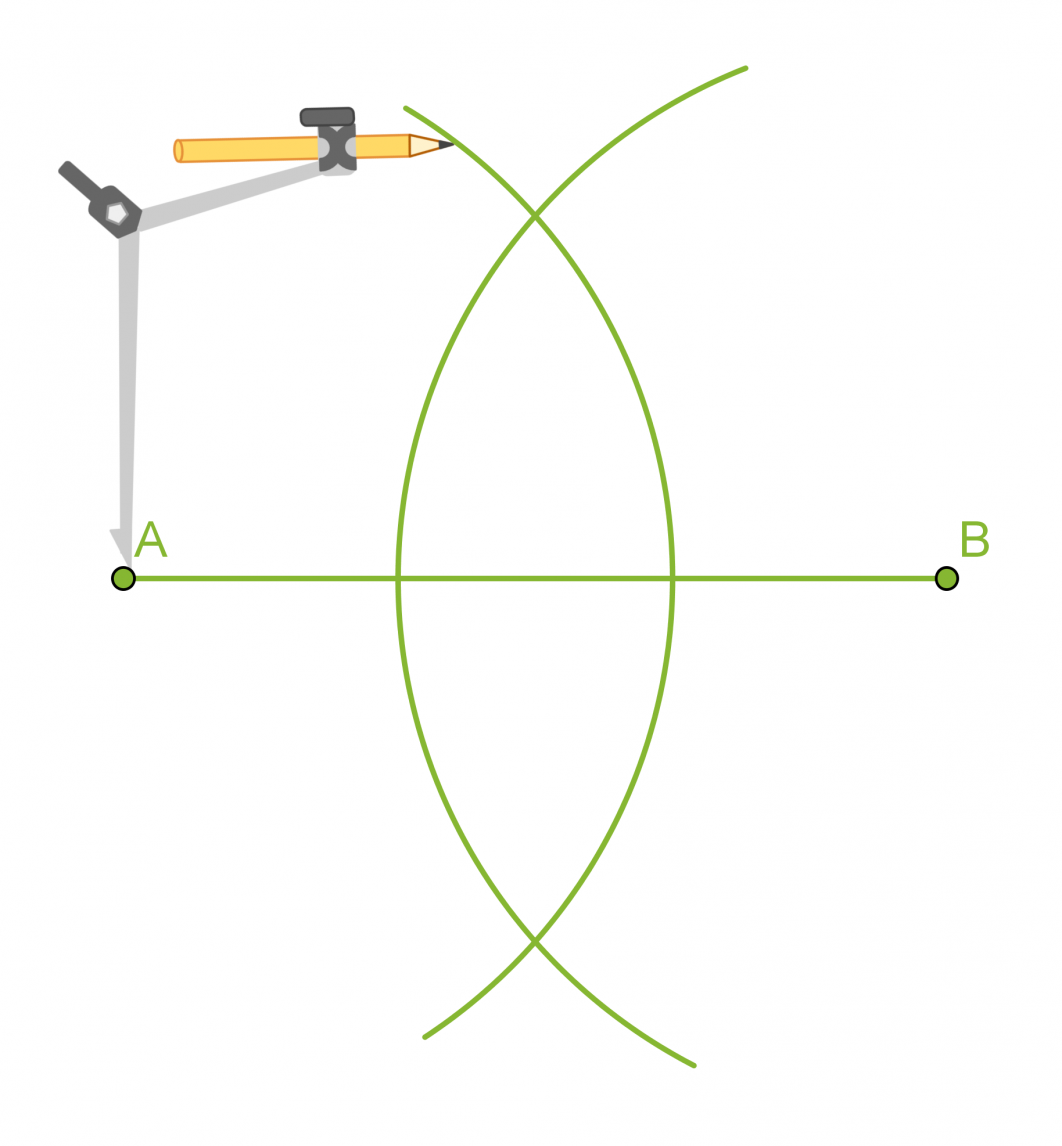
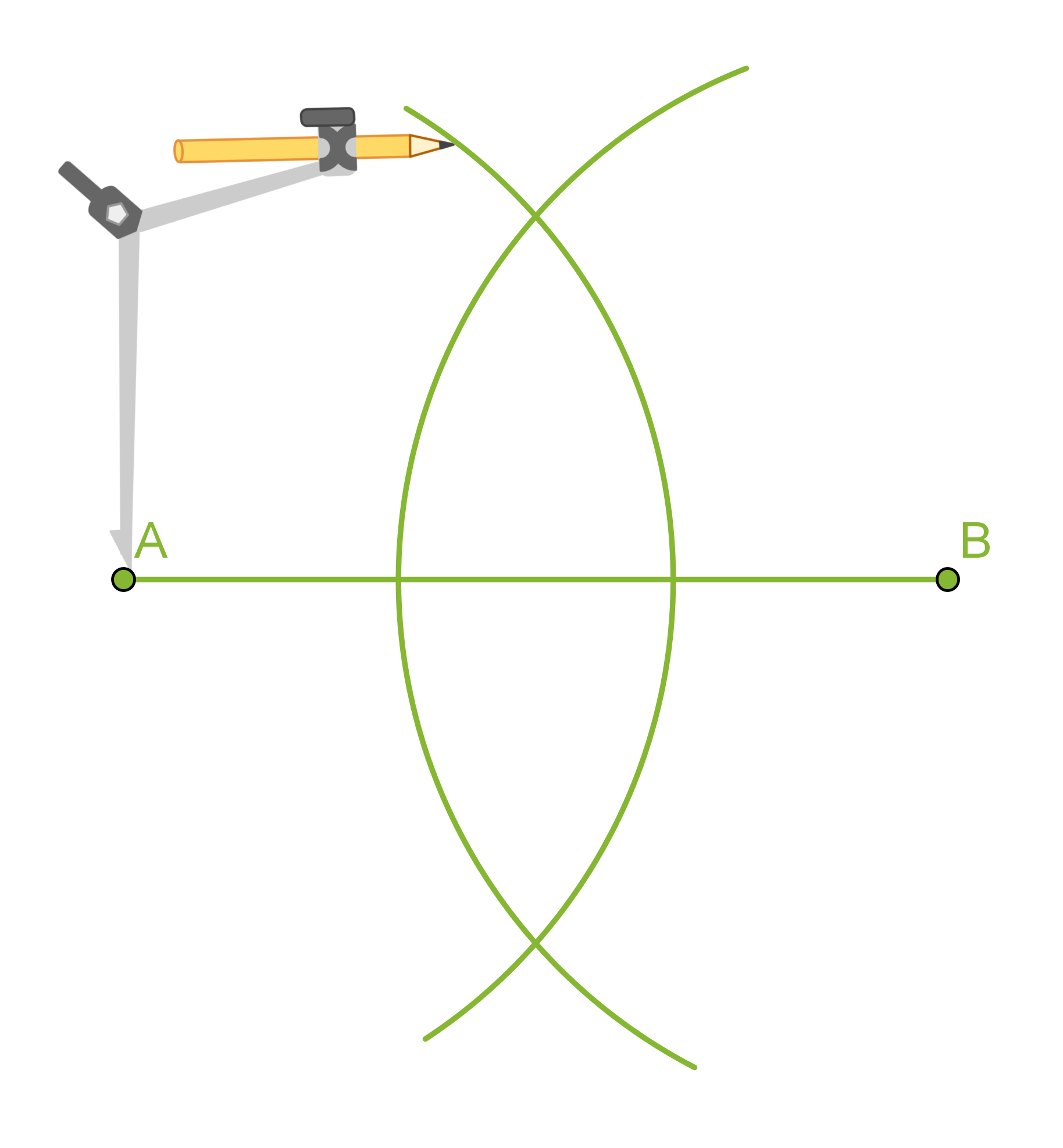
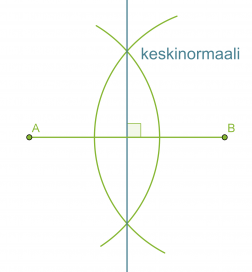
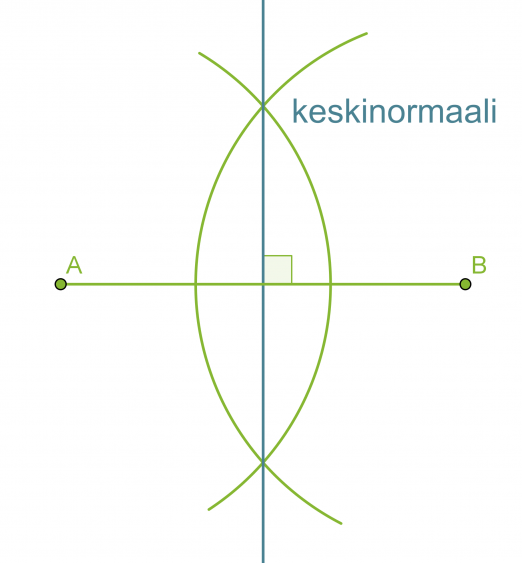
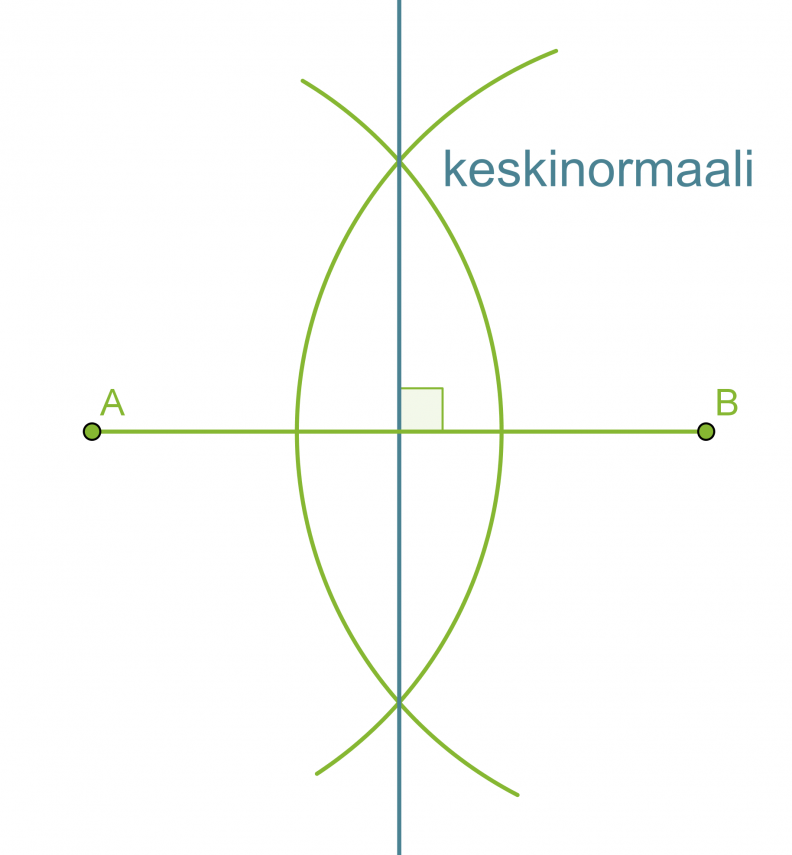
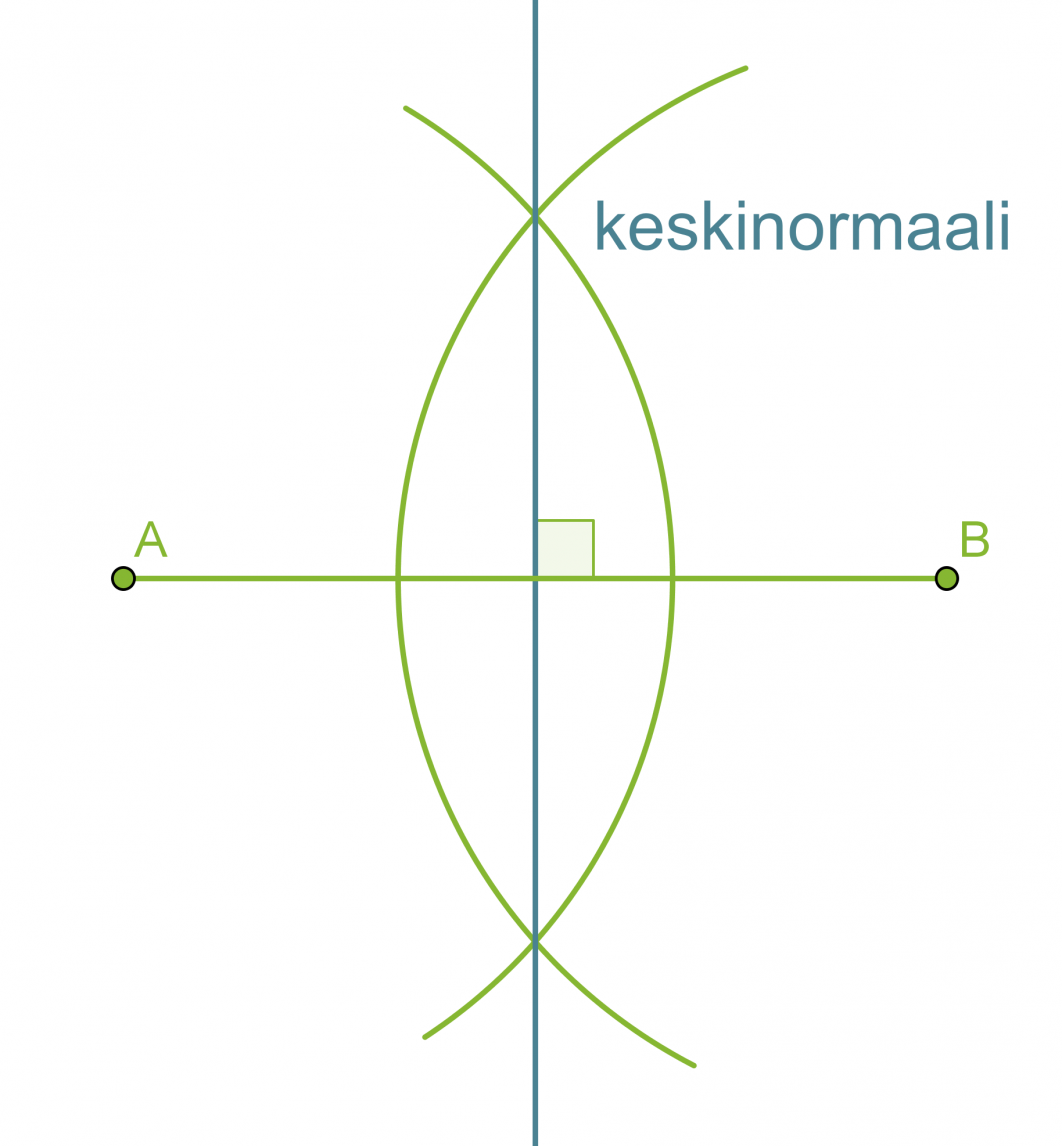
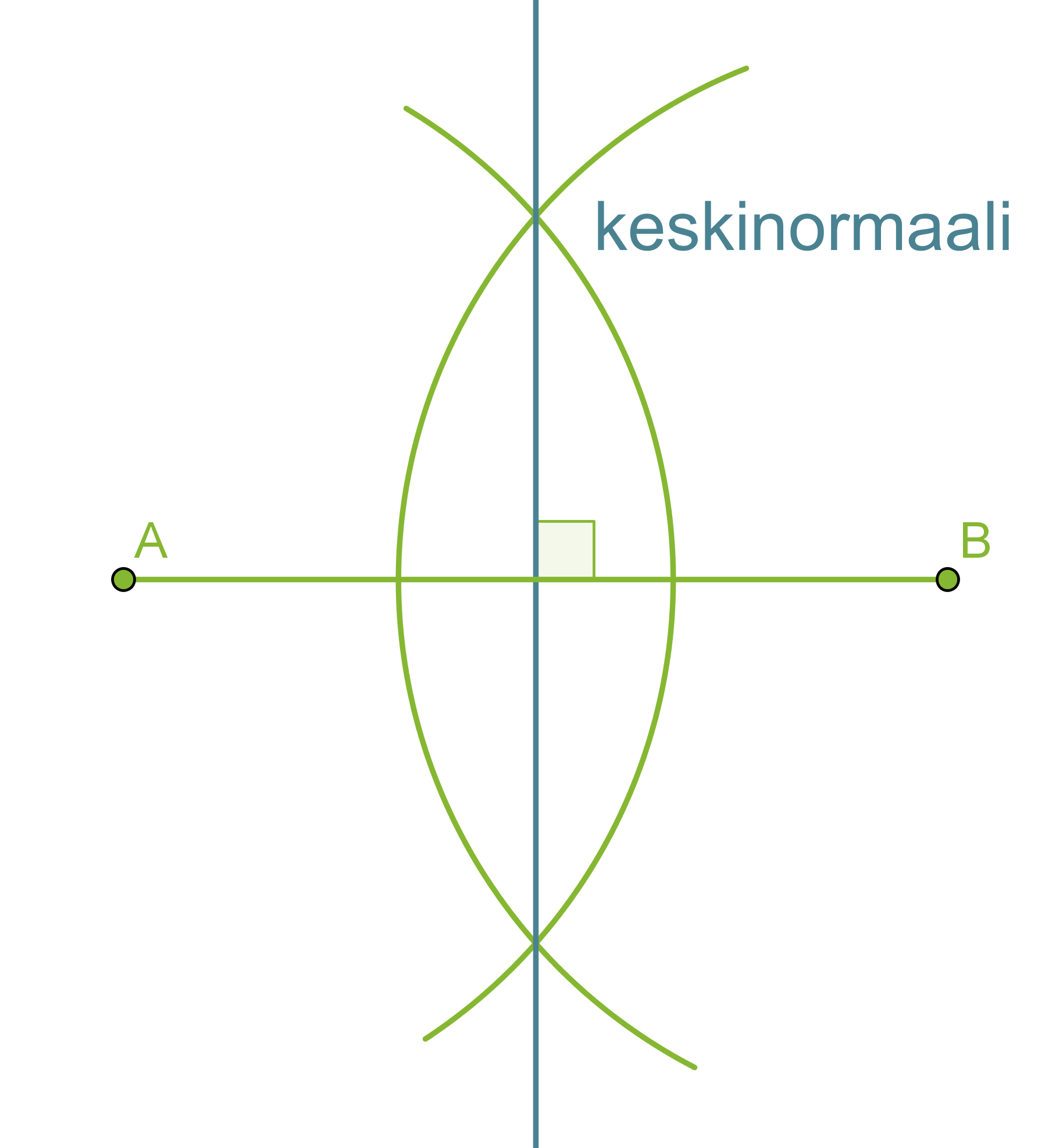
Janan keskinormaali on janan keskipisteeseen piirretty kohtisuora suora. Keskinormaali on niiden pisteiden muodostama suora, jotka ovat yhtä kaukana janan molemmista päätepisteistä.
Janan keskinormaalin piirtäminen
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
- Piirretään janan päätepisteet A ja B keskipisteinä sellaiset samansäteiset ympyrän kaaret, jotka leikkaavat toisensa.
- Piirretään suora, joka kulkee ympyränkaarien leikkauspisteiden kautta. Tämä suora on janan AB keskinormaali
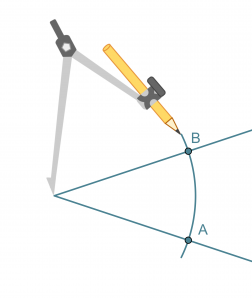
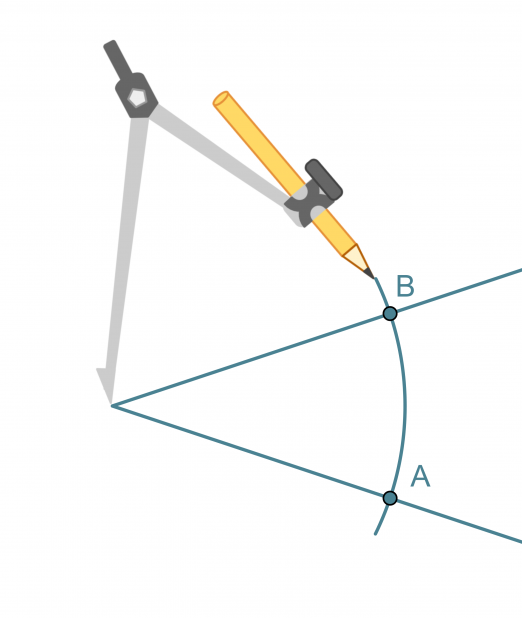
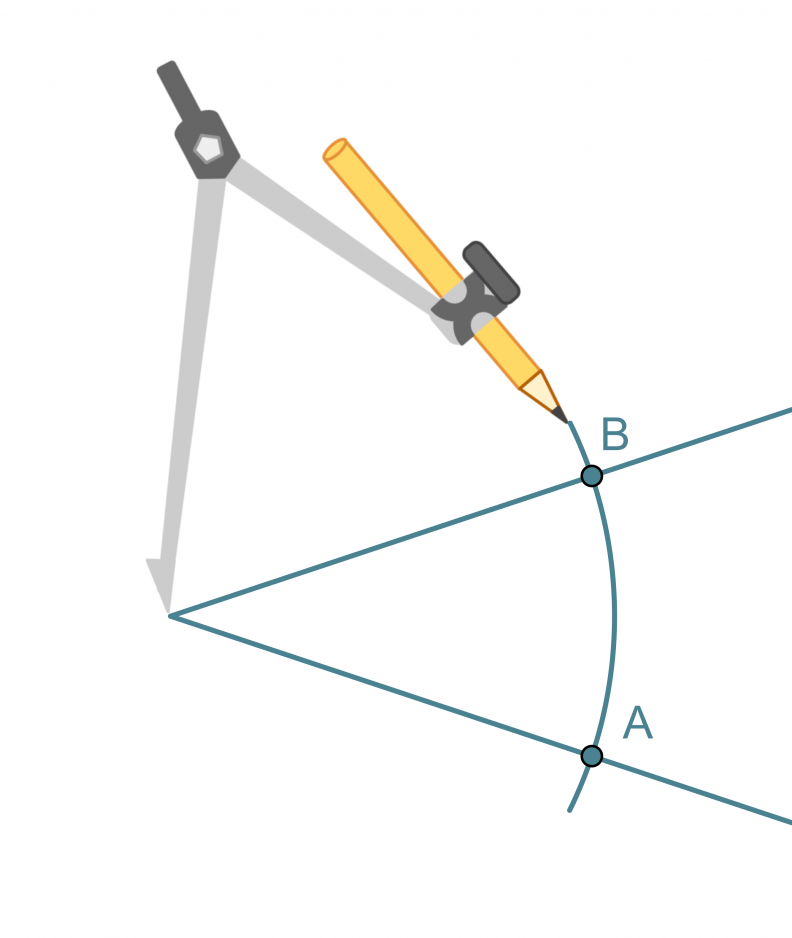
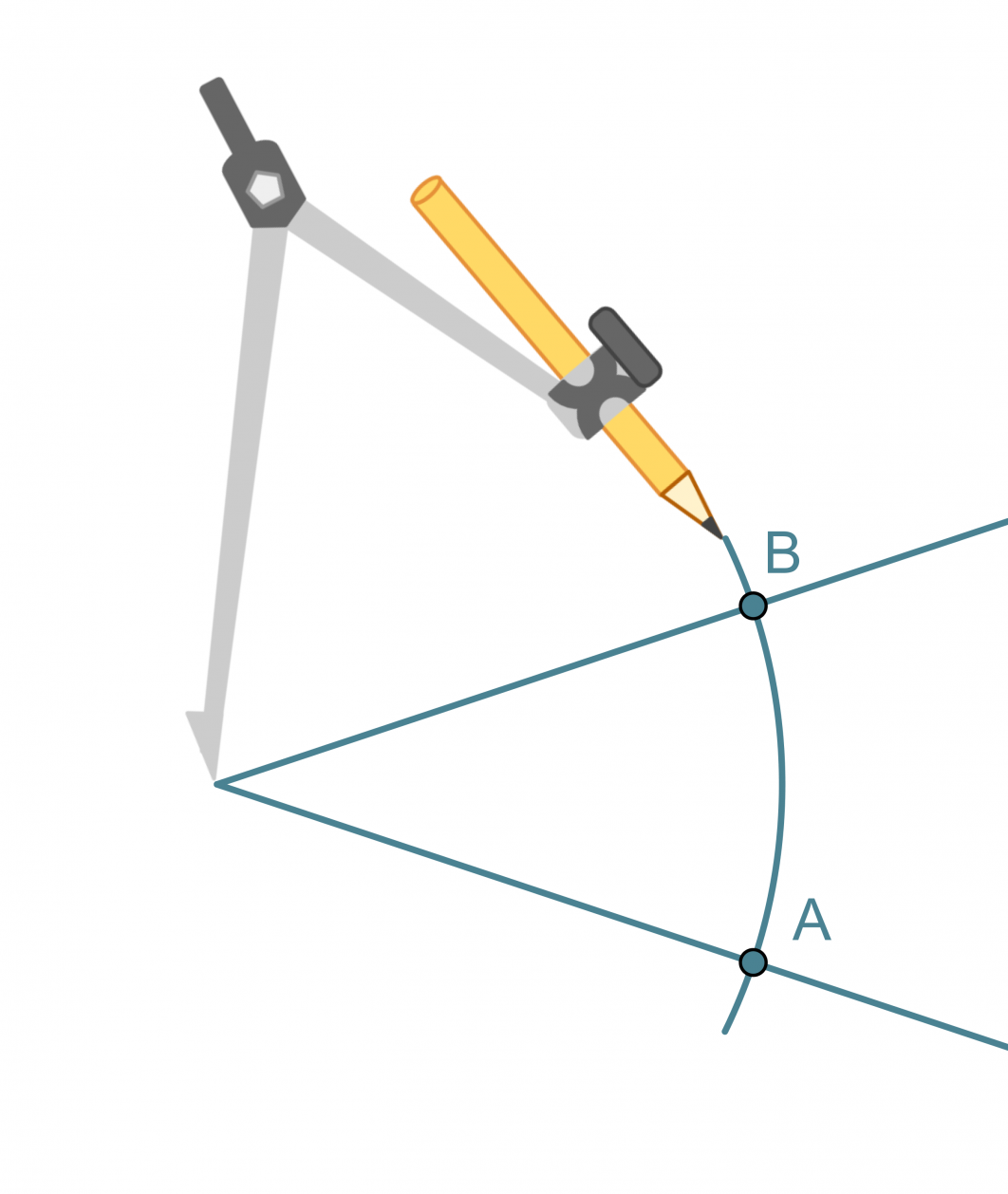
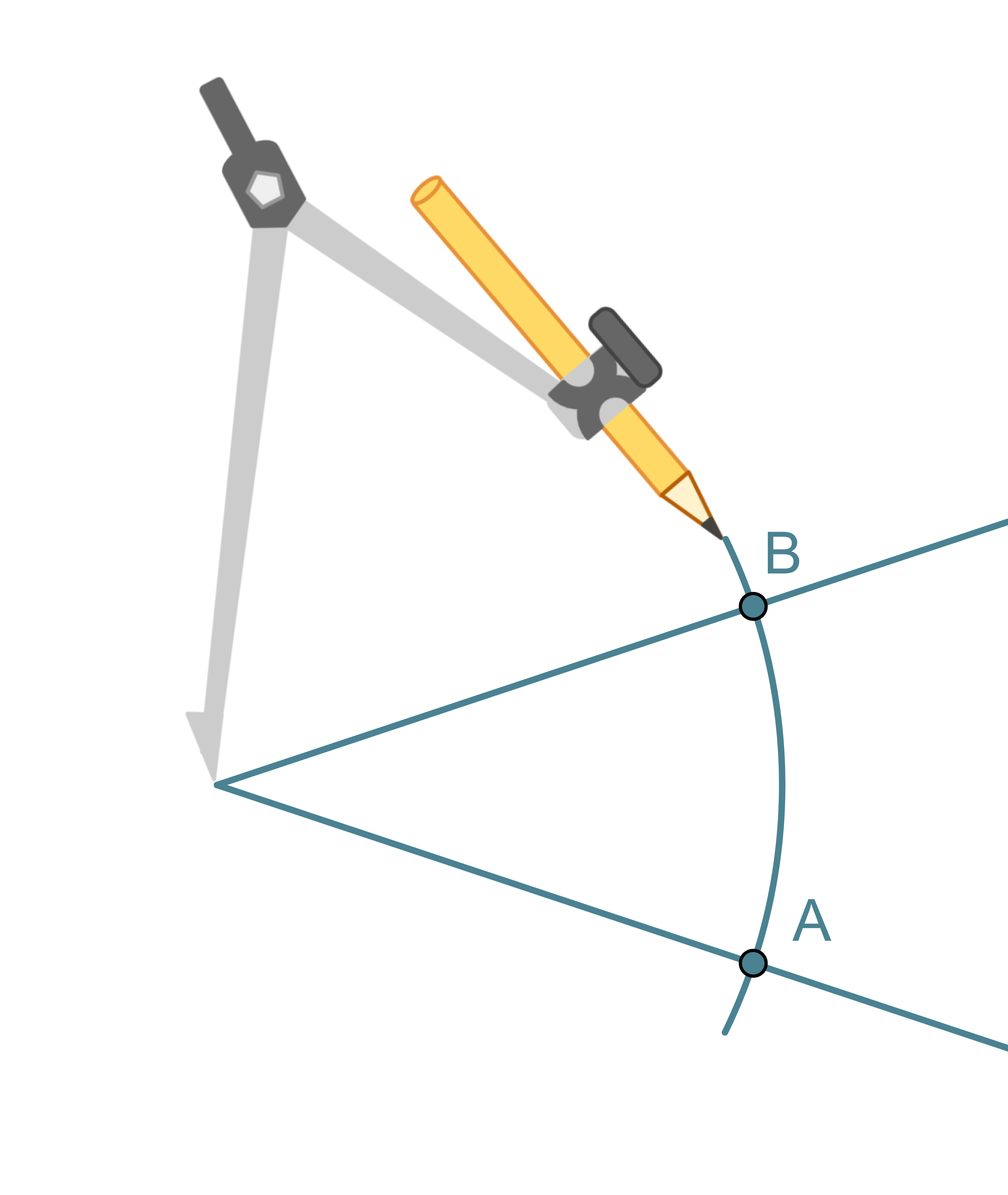
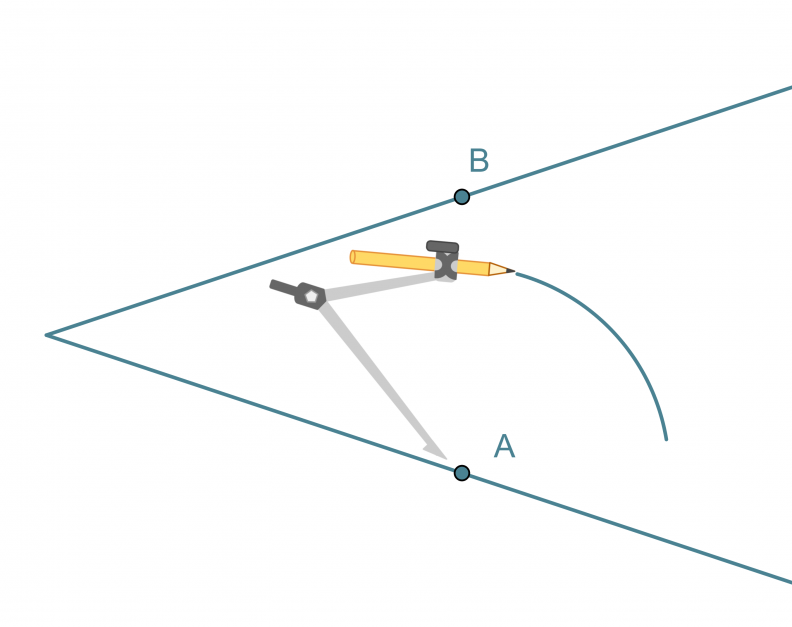
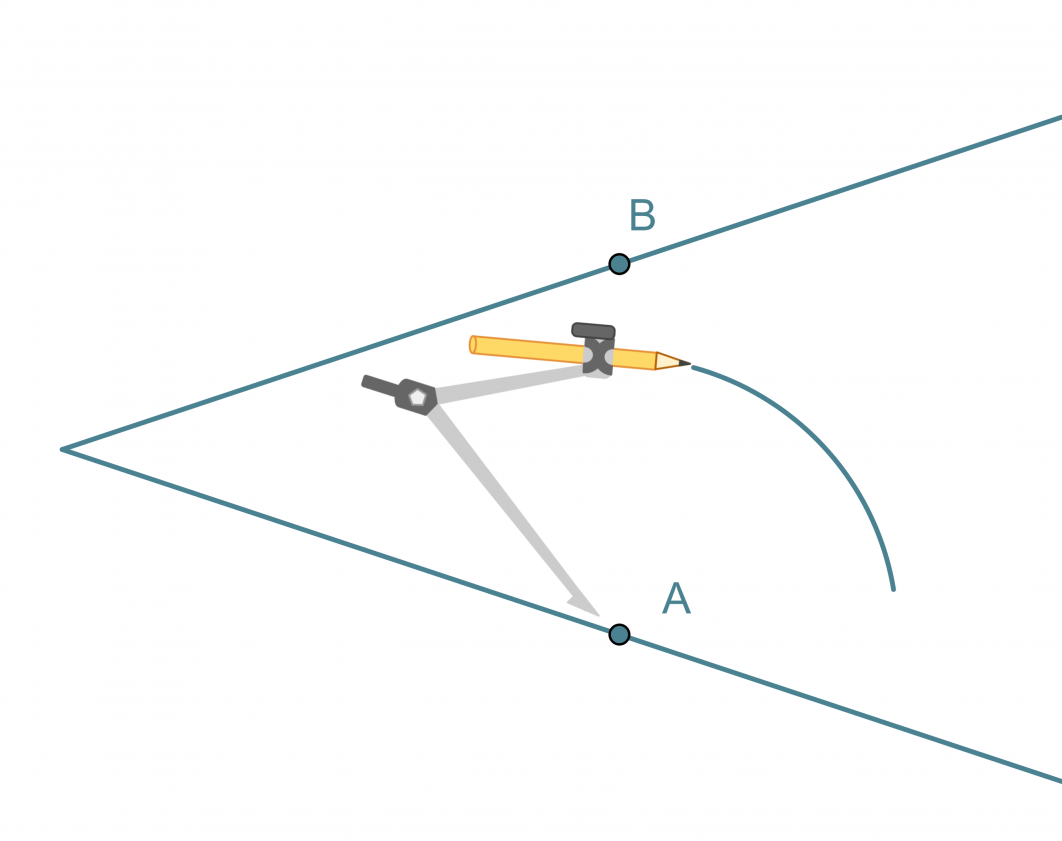
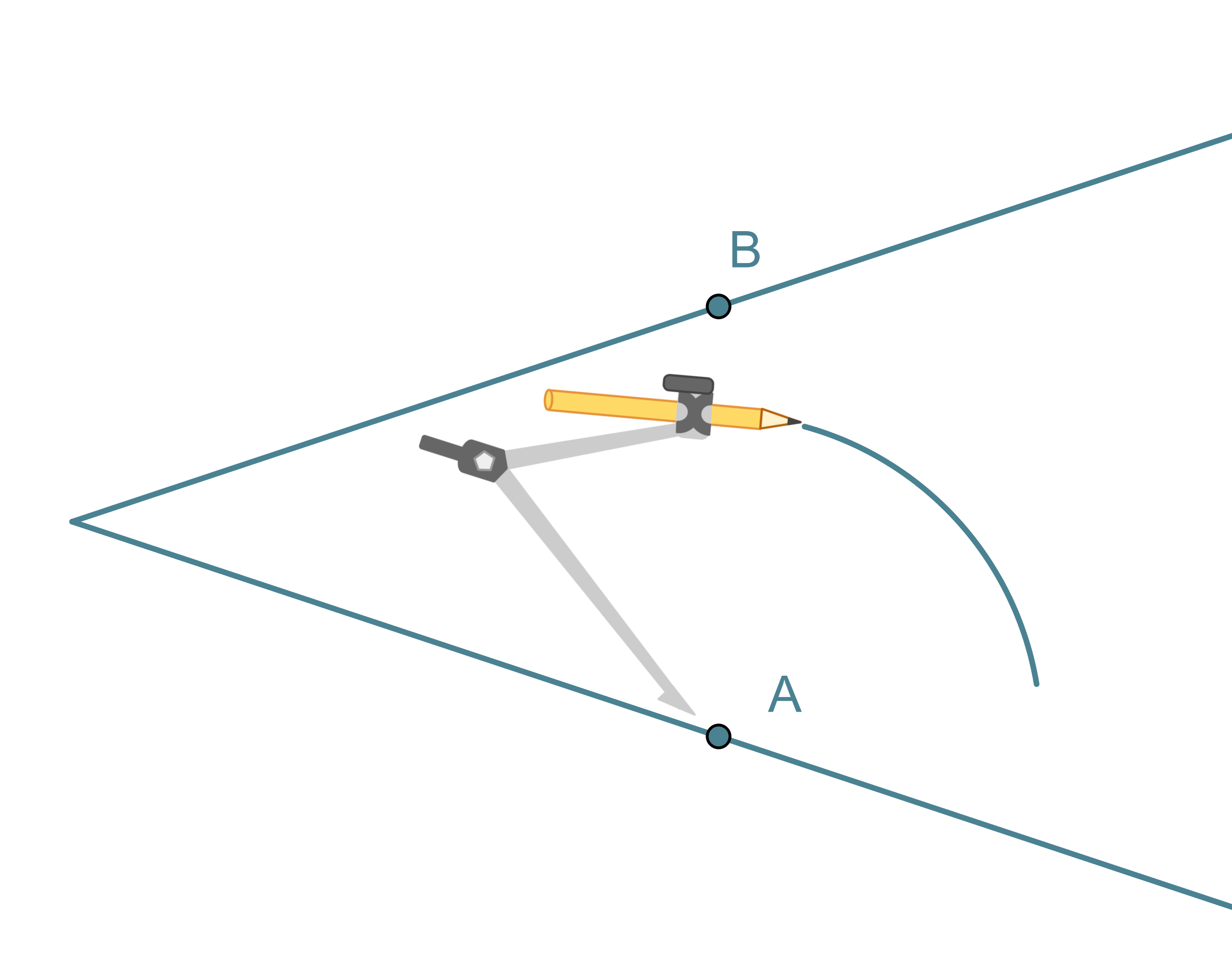
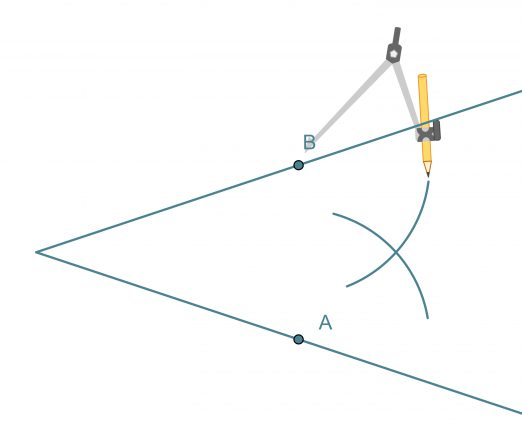
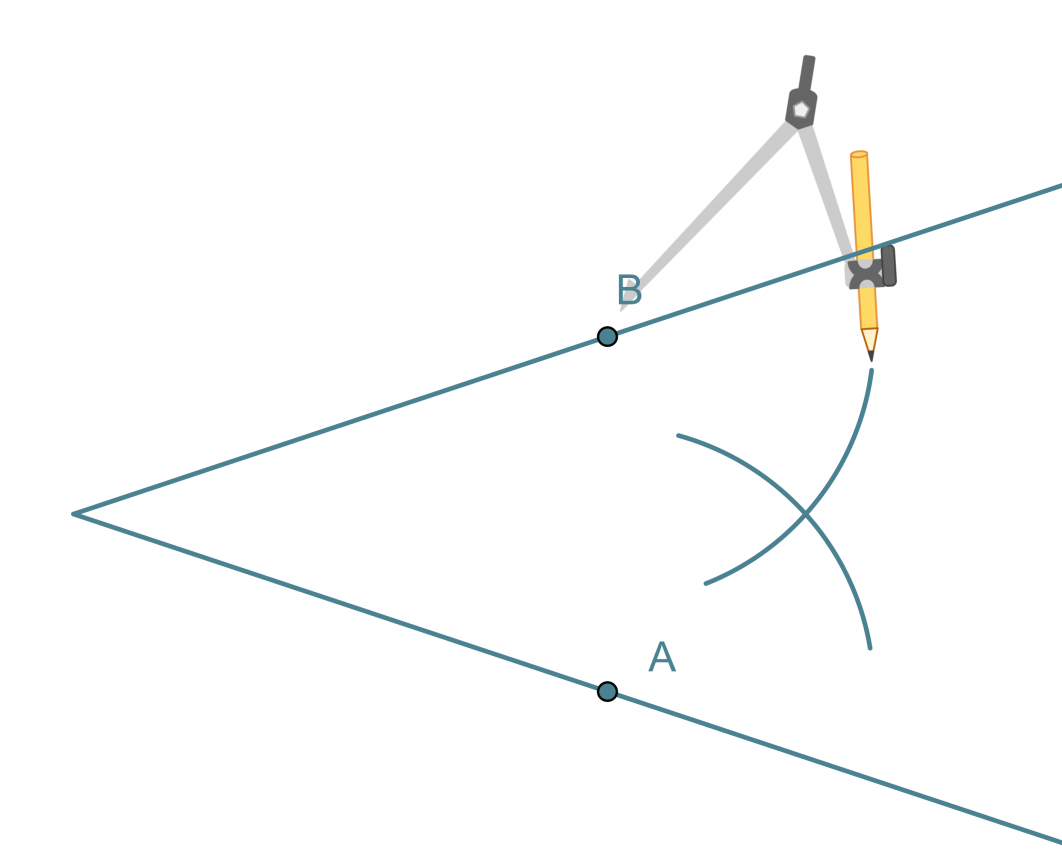
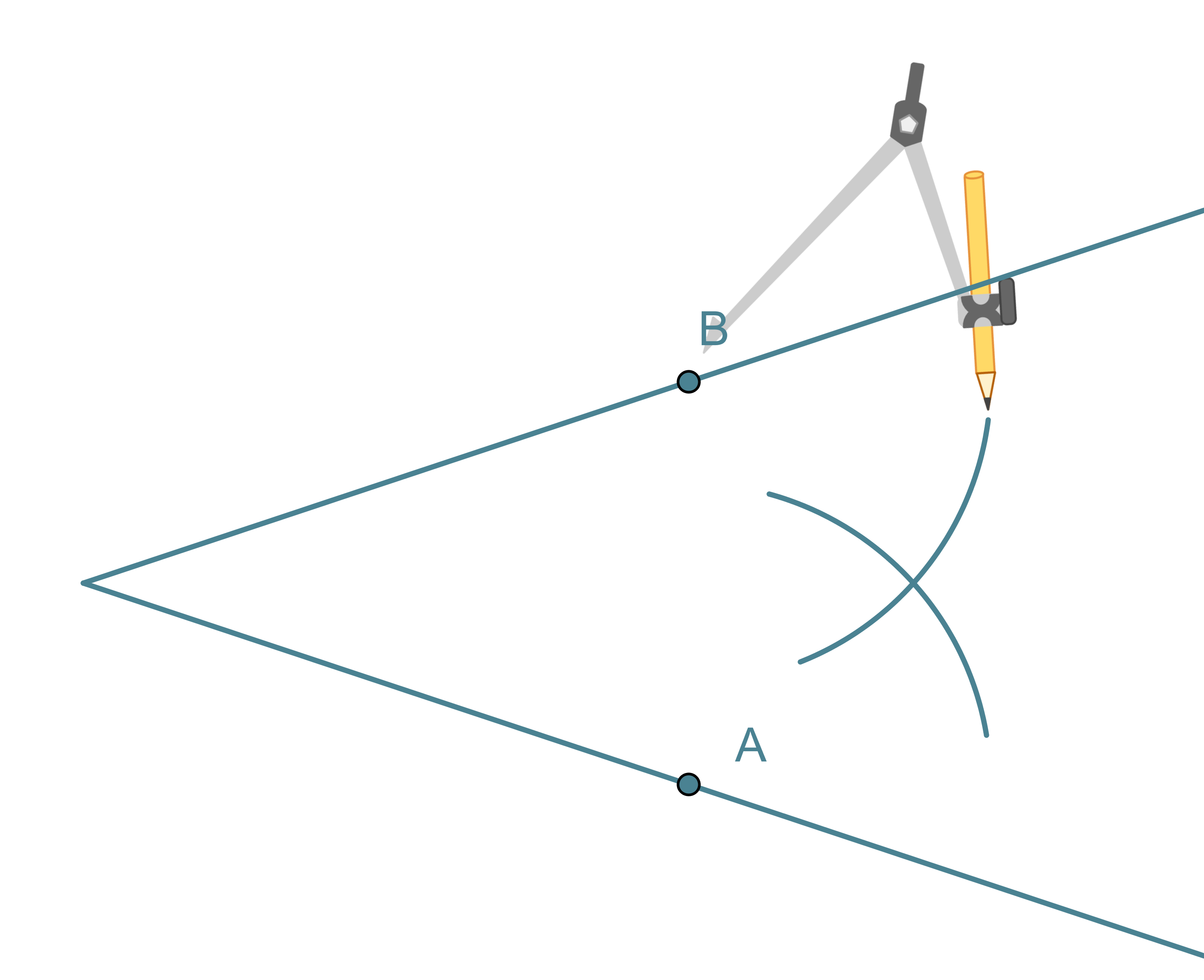
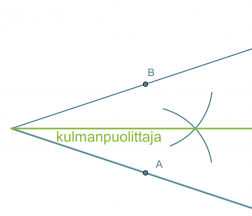
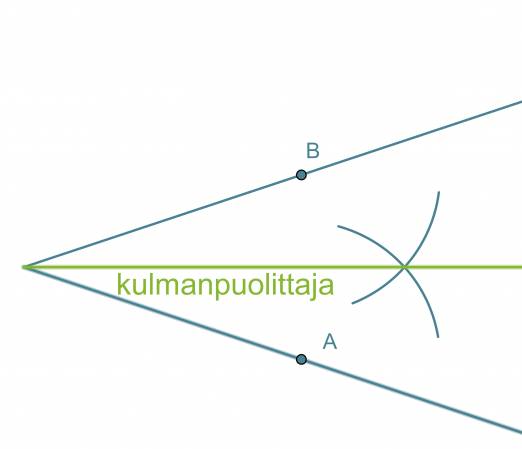
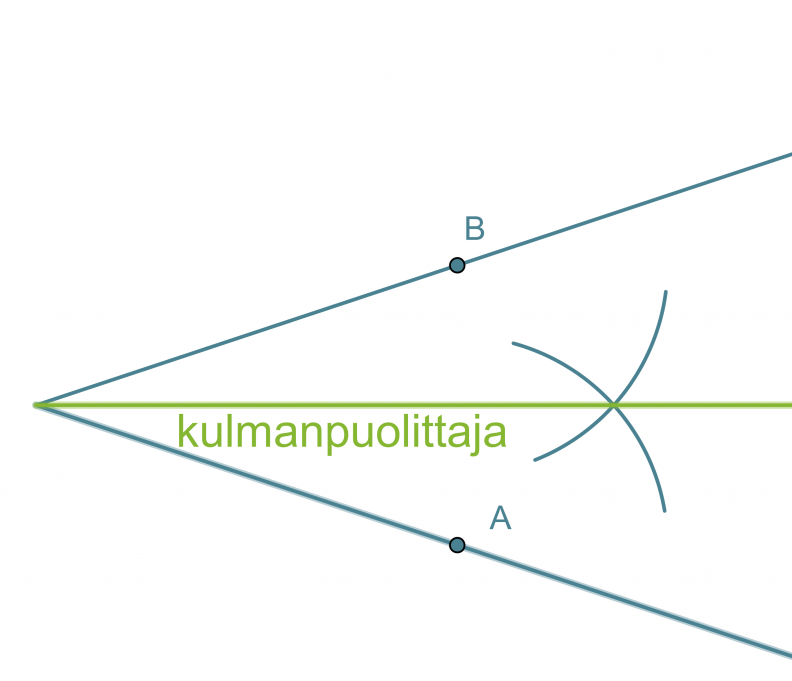
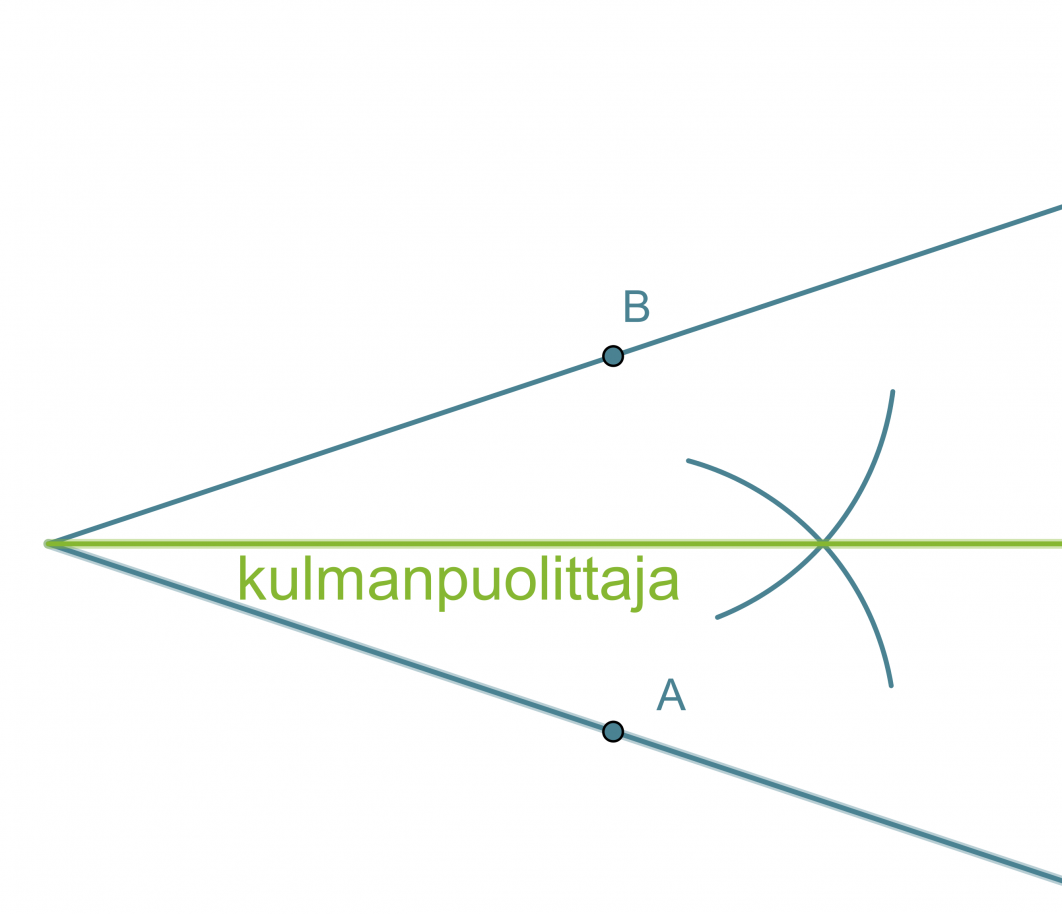
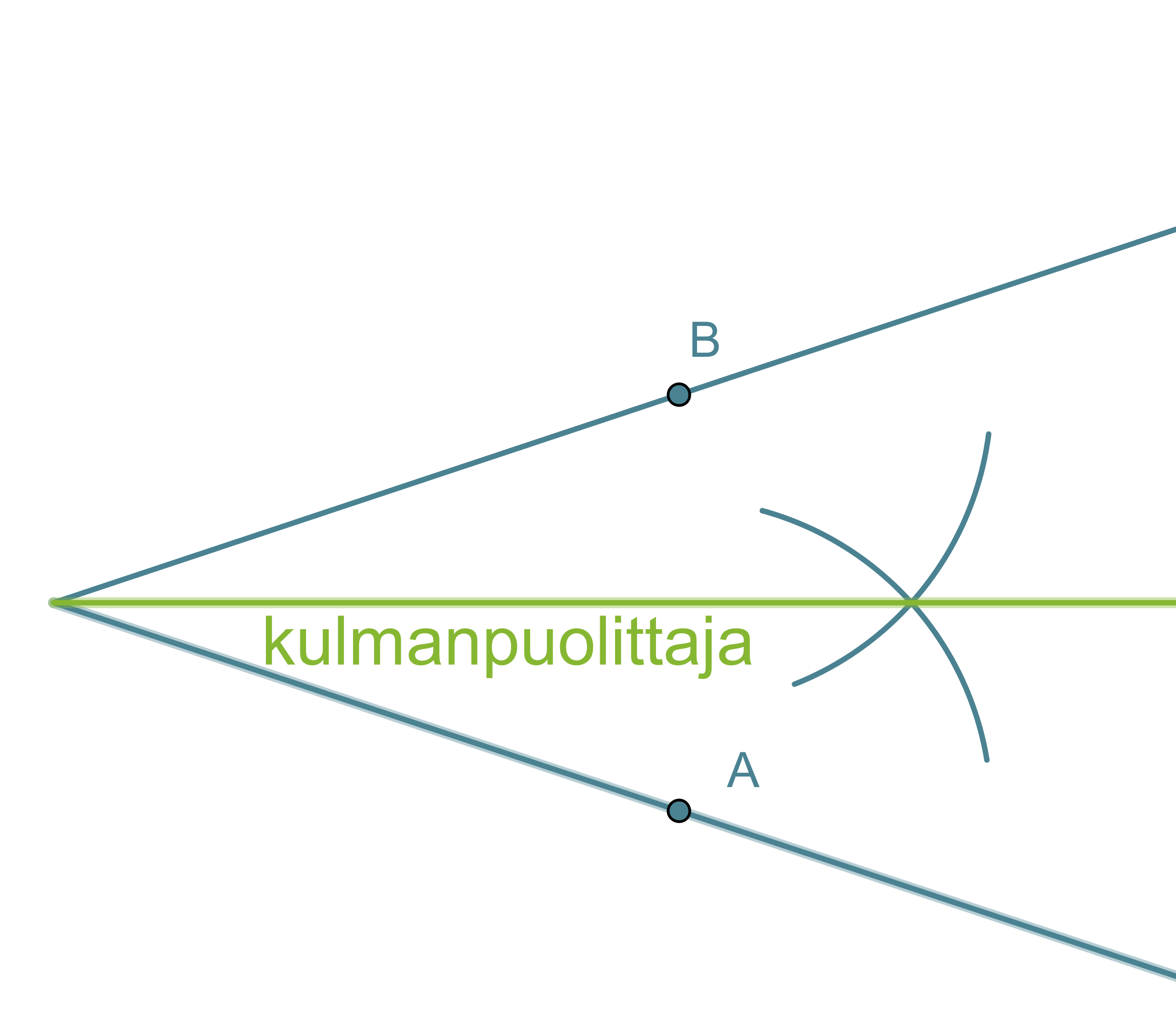
Kulman puolittaja on puolisuora, joka jakaa kulman kahteen yhtä suureen osaan. Kulman puolittaja on niiden pisteiden muodostama puolisuora, jotka ovat yhtä kaukana kummastakin kyljestä.
Kulman puolittajan piirtäminen
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
- Kulman kärki keskipisteenä piirretään ympyränkaari, joka leikkaa kulman molemmat kyljet.
- Leikkauspisteet A ja B keskipisteinä piirretään sellaiset samansäteiset ympyränkaaret, että ne leikkaavat toisensa kulman aukeamassa.
- Ympyränkaarien leikkauspiste yhdistetään kulman kärkipisteeseen. Tämä puolisuora on kulman puolittaja.
Korkeusjana, mediaani, kulman puolittaja ja sivun keskinormaali ovat kolmioon liittyviä janoja ja suoria. Niillä jokaisella on yllättävä ominaisuus.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
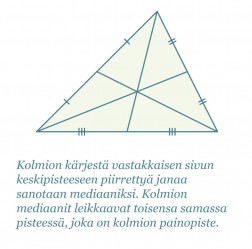
Klikkaa kuva suuremmaksi!
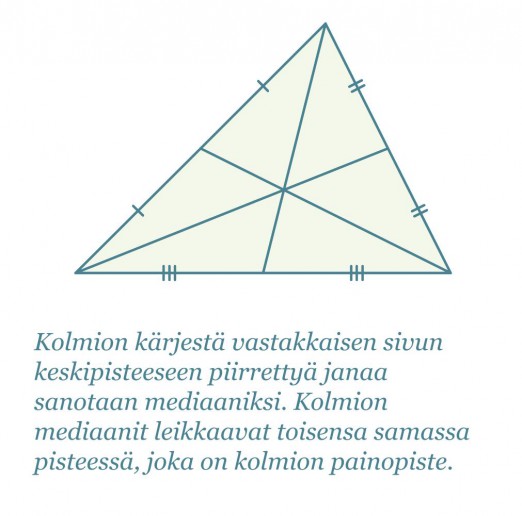
Klikkaa kuva suuremmaksi!
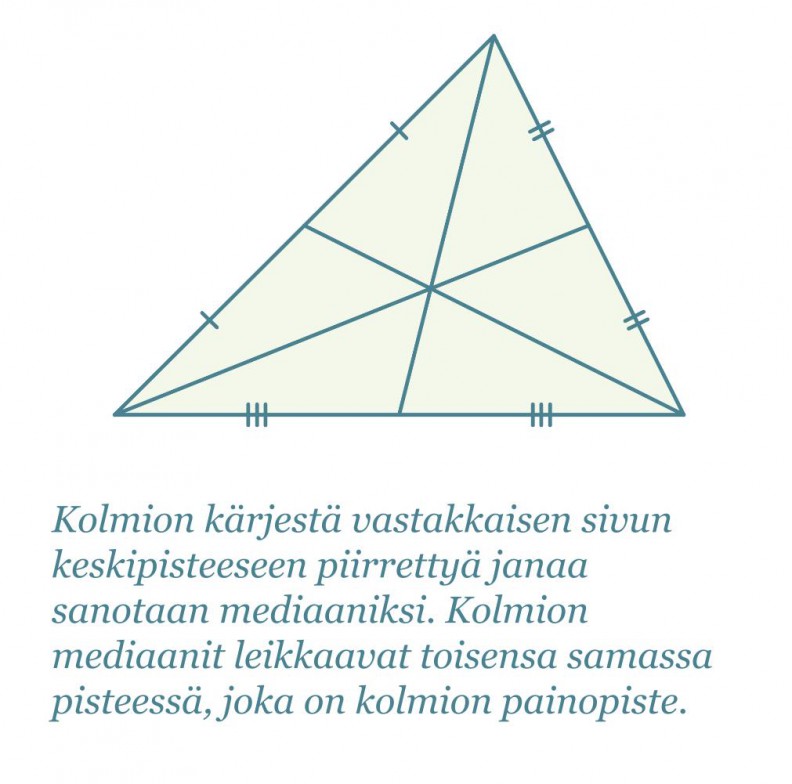
Klikkaa kuva suuremmaksi!
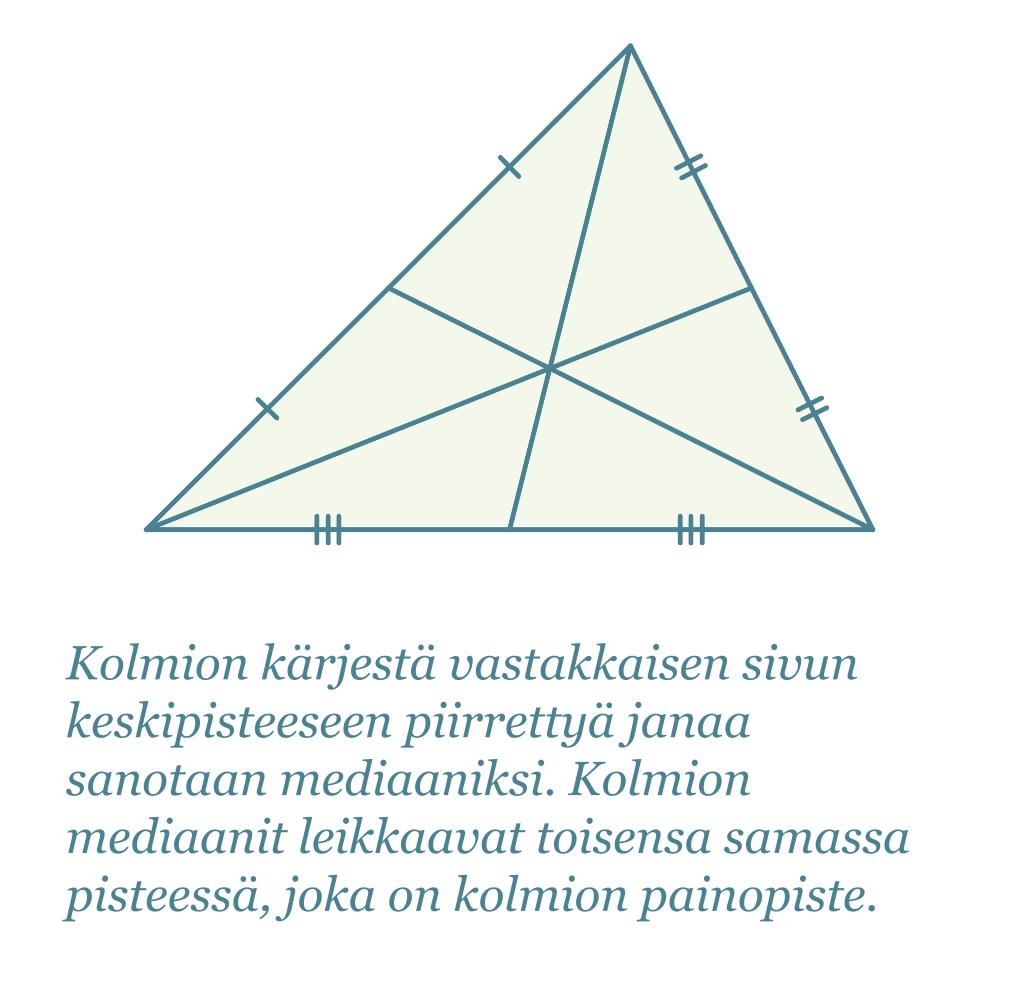
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
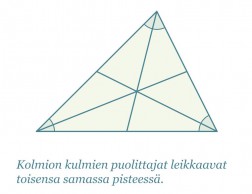
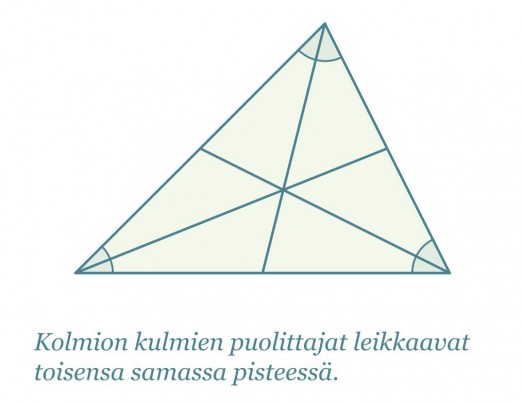
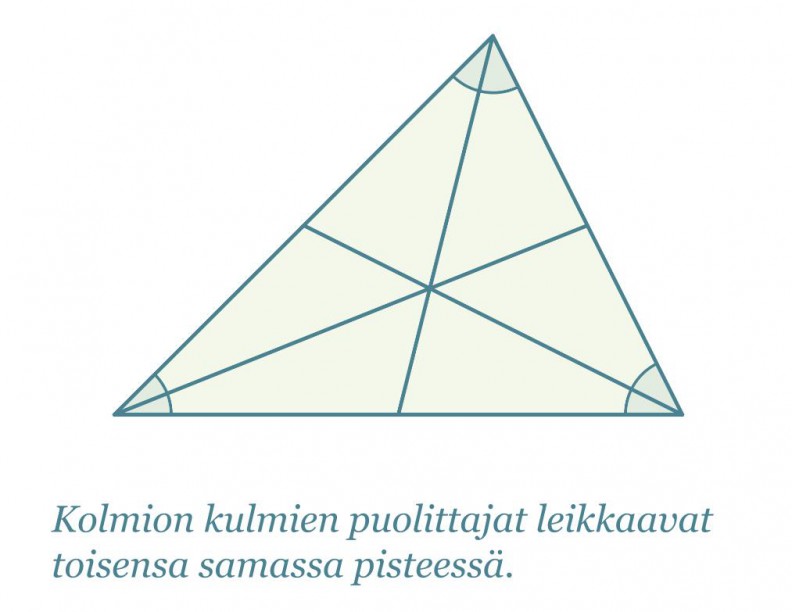
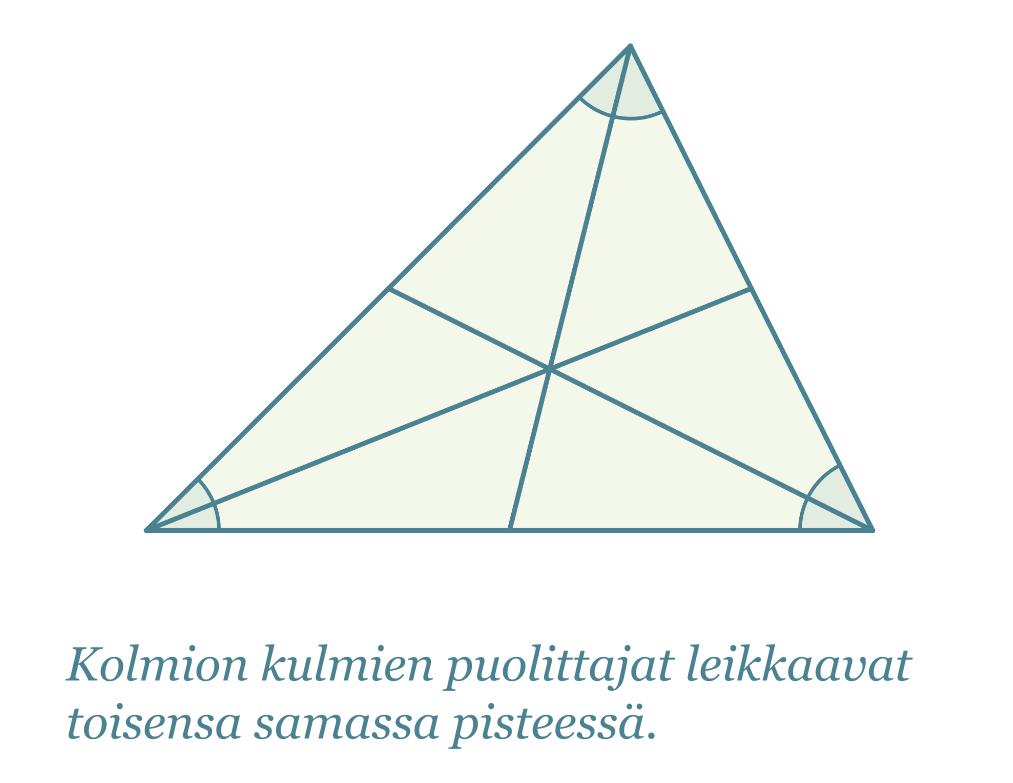
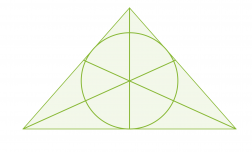
Kolmannesta merkillisestä pisteestä seuraa, että jokaisen kolmion sisään voidaan piirtää ympyrä siten, että se sivuaa jokaista kolmion sivua. Kolmion kulmien puolittajien leikkauspiste on kolmion sisään piirretyn ympyrän keskipiste.
Klikkaa kuva suuremmaksi!
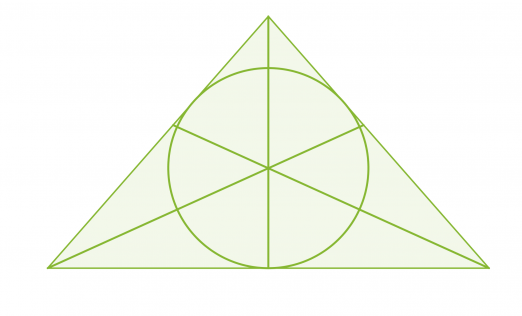
Klikkaa kuva suuremmaksi!
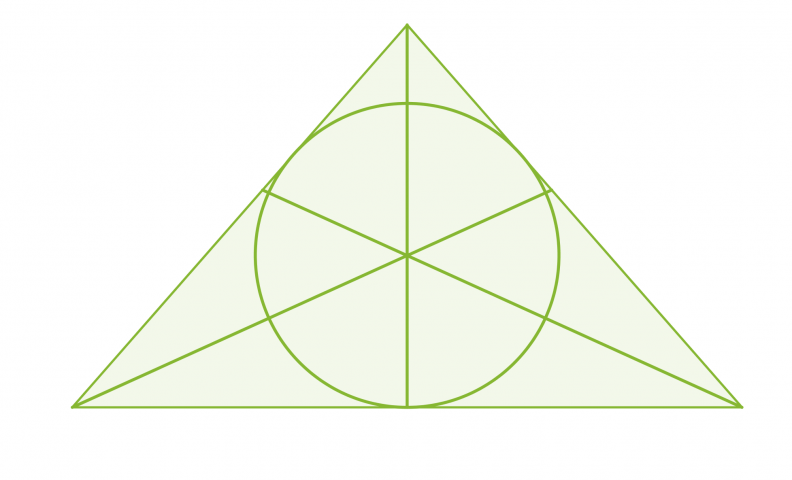
Klikkaa kuva suuremmaksi!
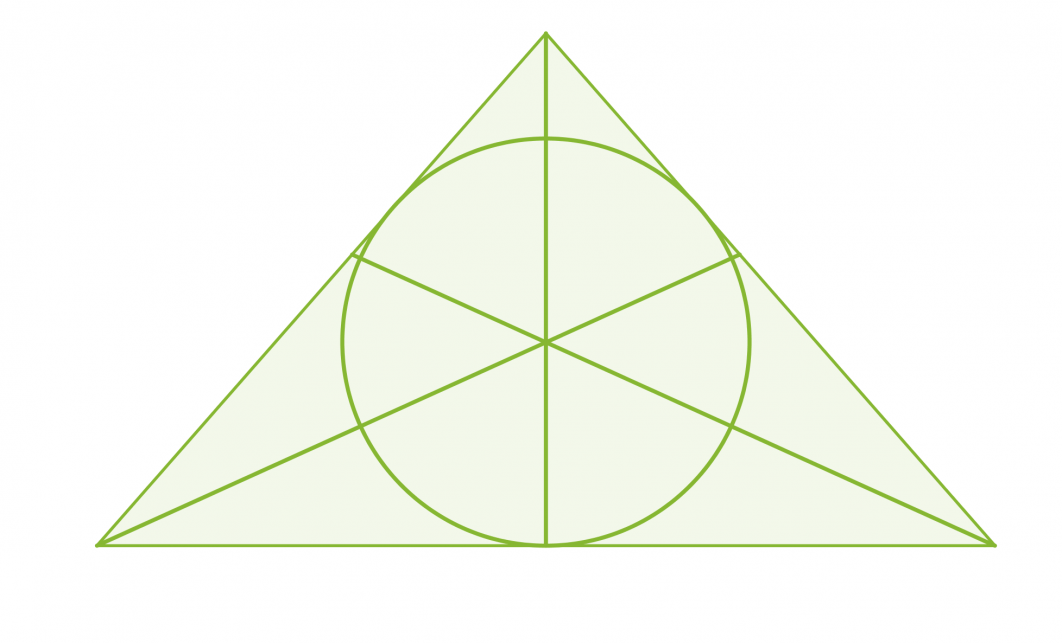
Klikkaa kuva suuremmaksi!
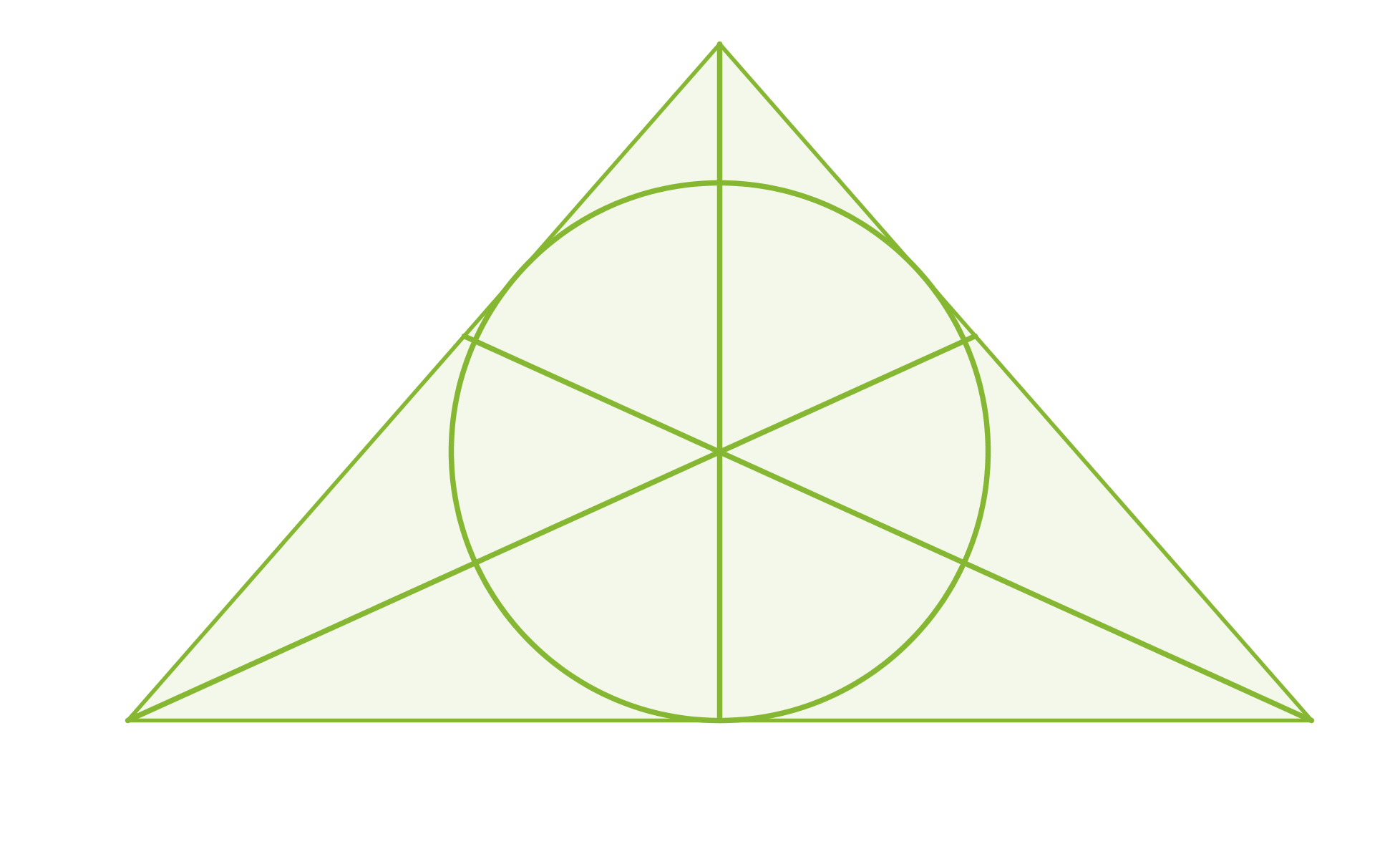
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
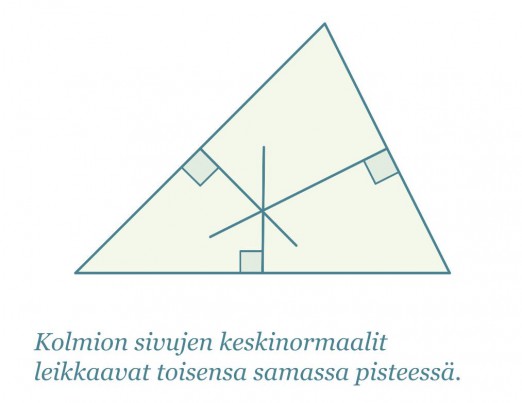
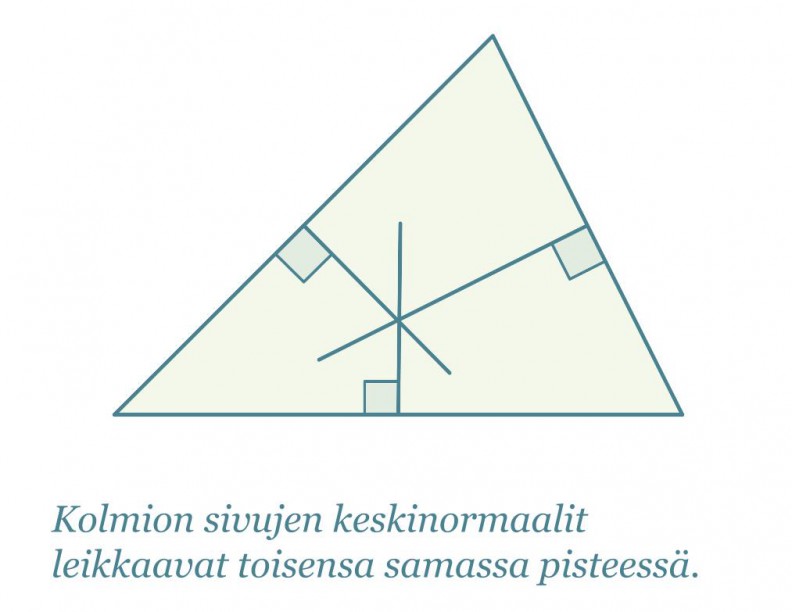
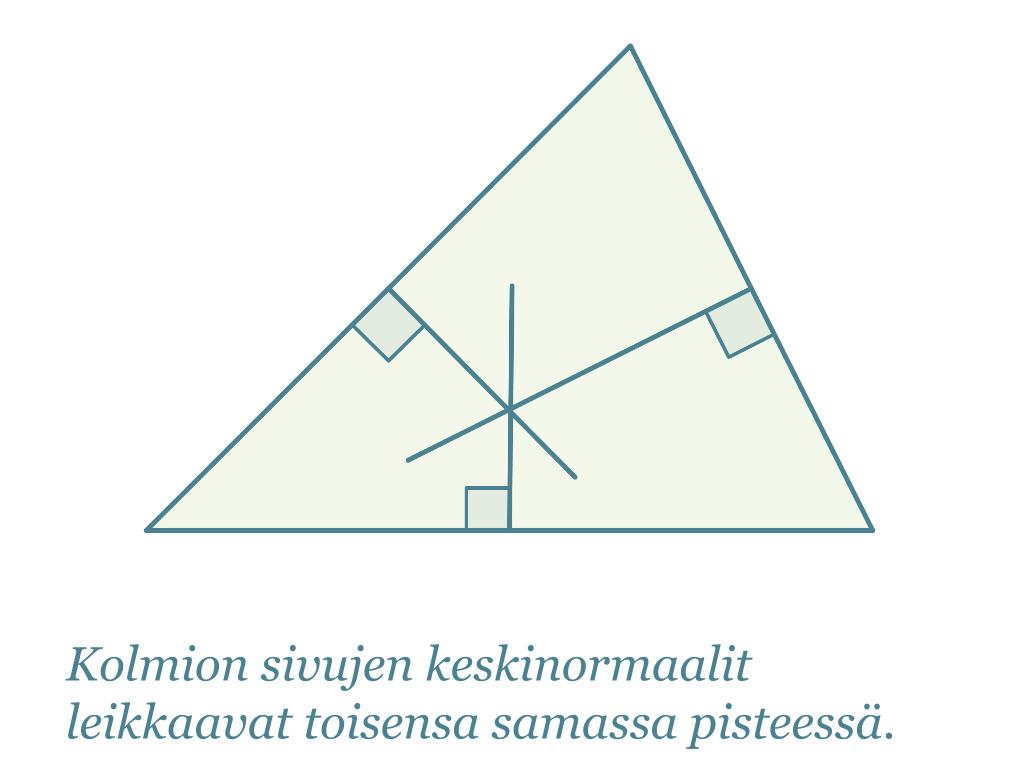
Neljännestä merkillisestä pisteestä seuraa, että jokaisen kolmion ympäri voidaan piirtää ympyrä siten, että jokainen kolmion kärjistä sijaitsee ympyrän kehällä. Kolmion keskinormaalien leikkauspiste on kolmion ympäri piirretyn ympyrän keskipiste.
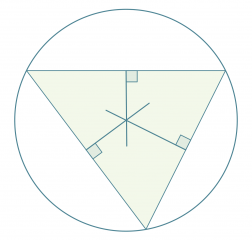
Klikkaa kuva suuremmaksi!
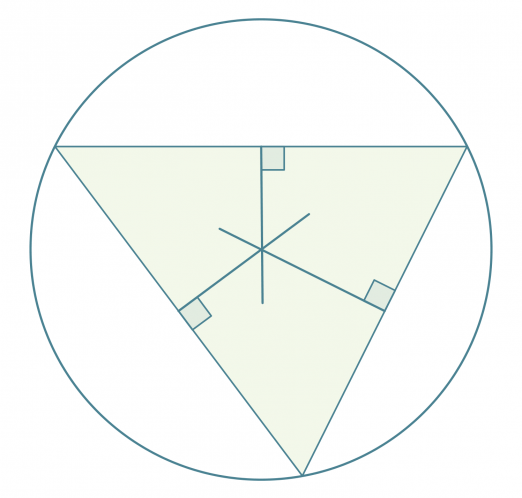
Klikkaa kuva suuremmaksi!
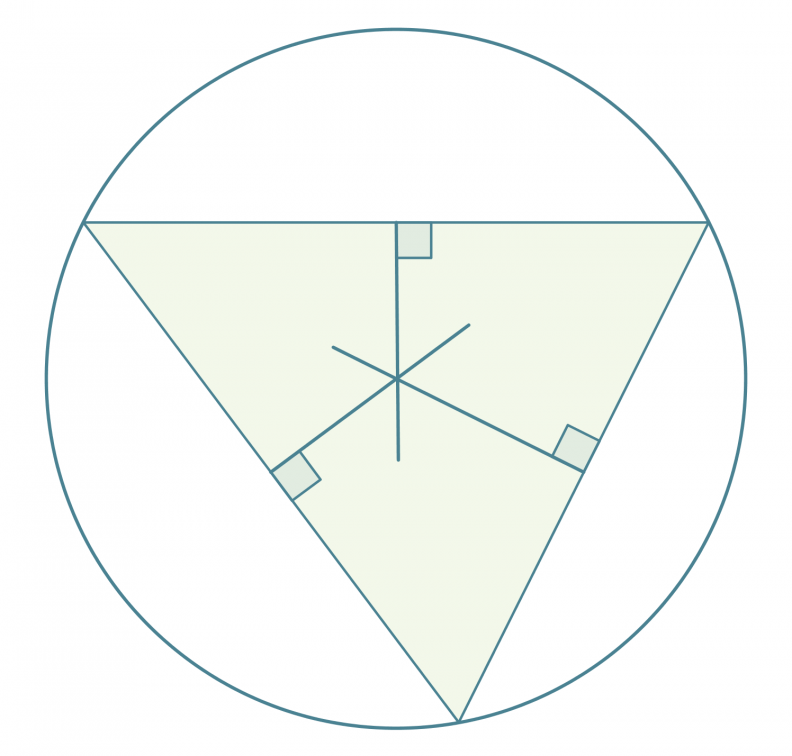
Klikkaa kuva suuremmaksi!
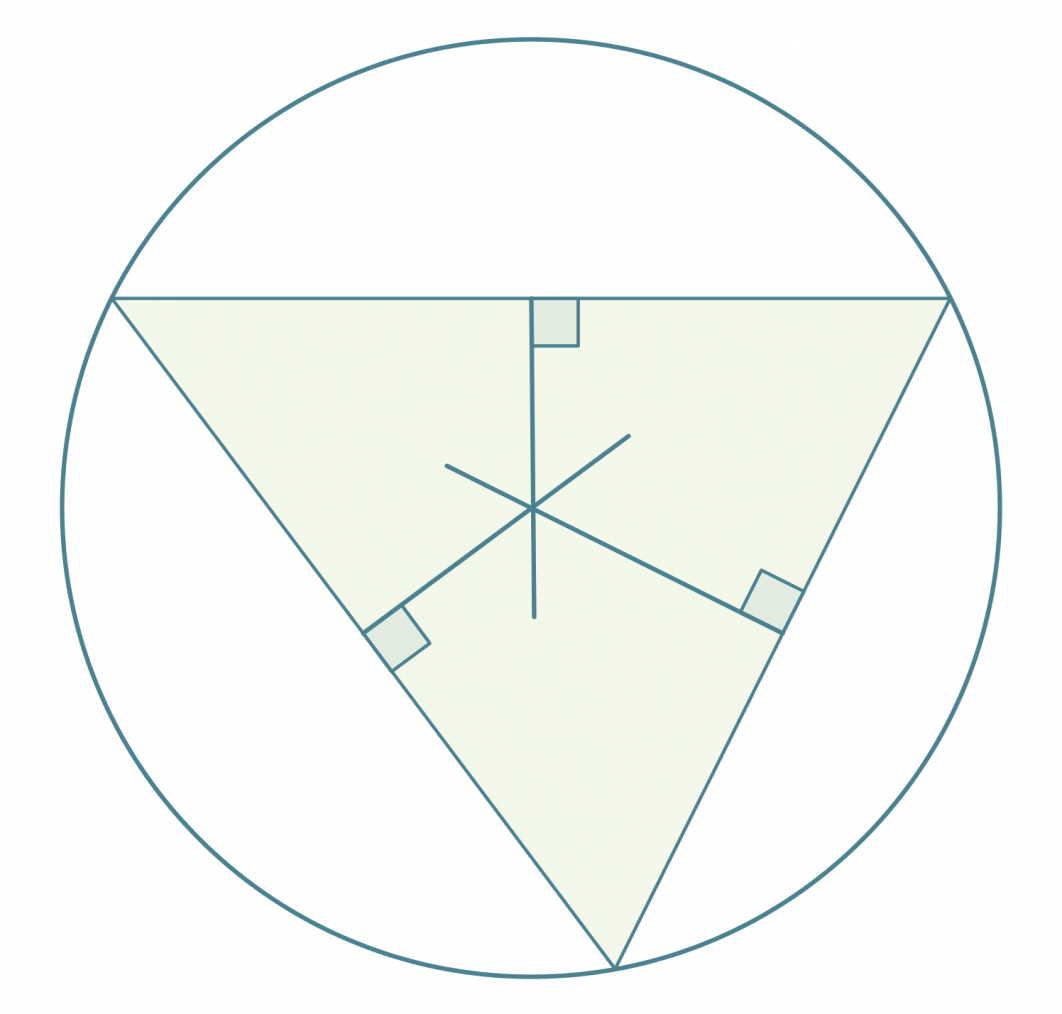
Klikkaa kuva suuremmaksi!
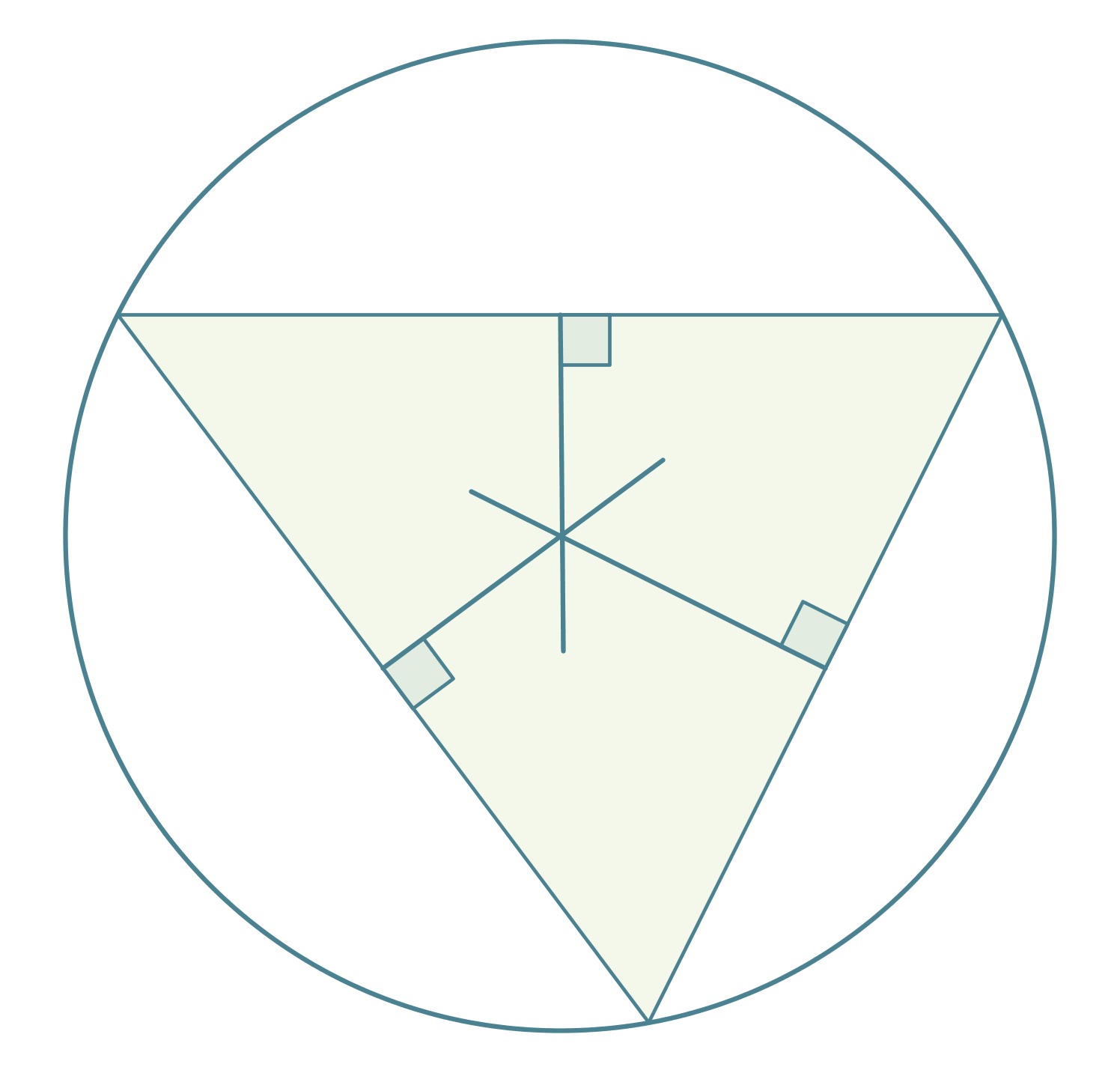
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
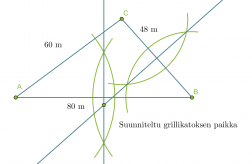
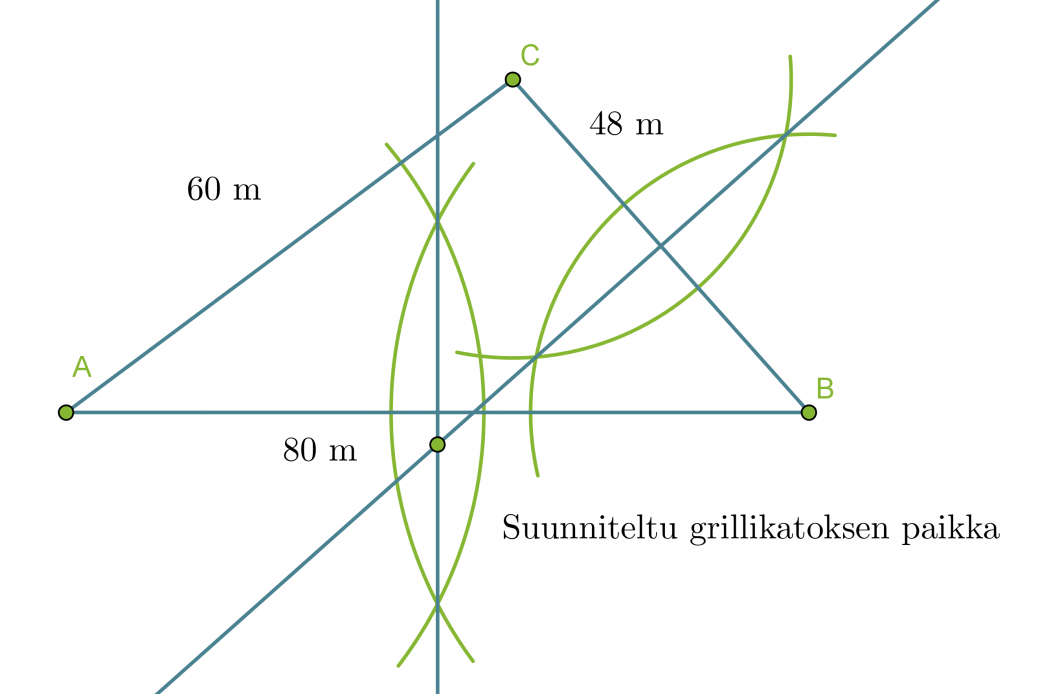
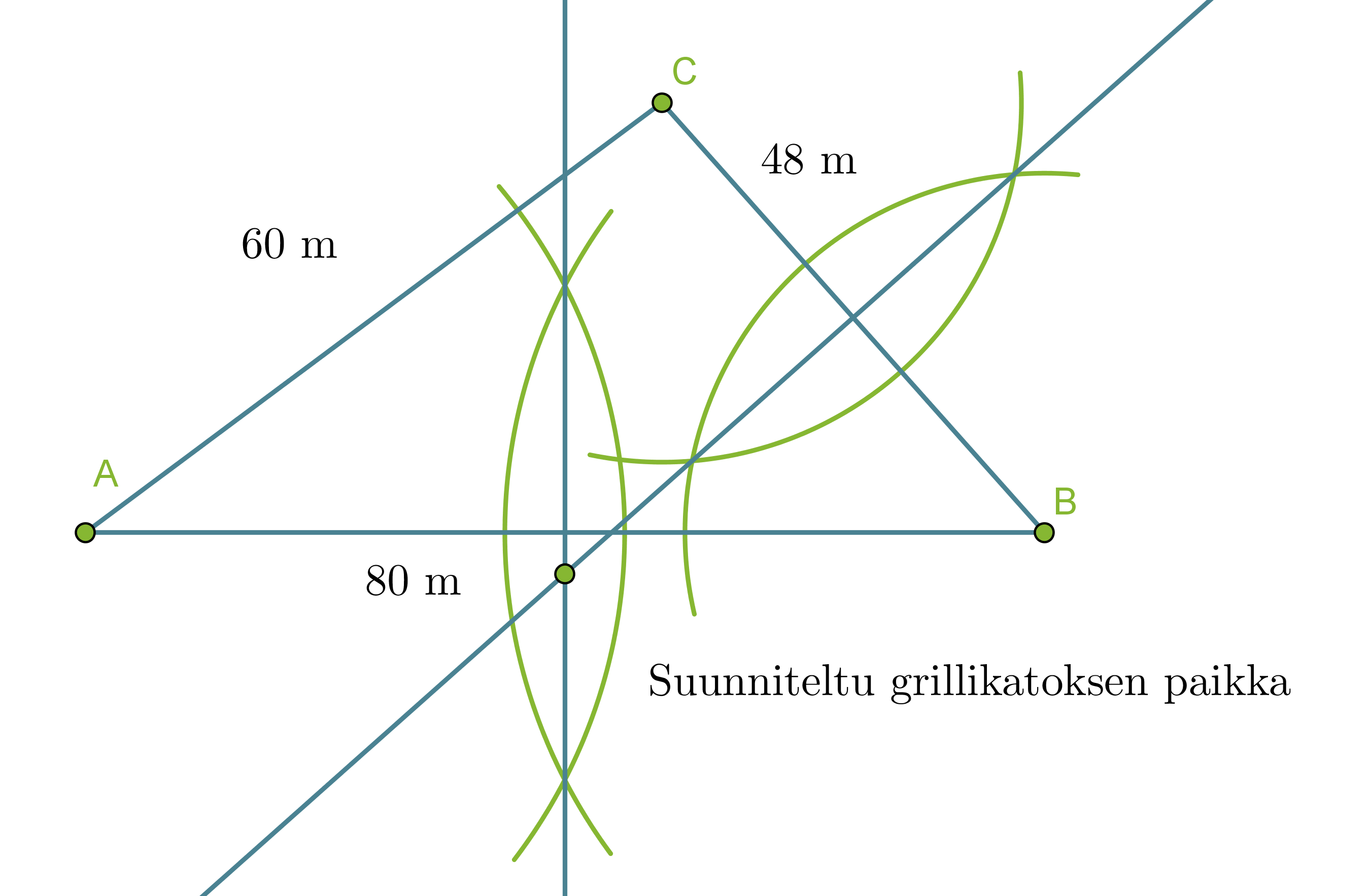
Asunto-osakeyhtiössä on kolme taloa, jotka omistavat pihan yhdessä. Pihalle rakennetaan yhteinen grillikatos. Mihin se pitäisi sijoittaa, jotta jokaiselta talolta olisi sinne yhtä pitkä matka? Piirrä kuva, jossa ilmenee paikka, kun talojen väliset etäisyydet ovat 48 m, 60 m ja 80 m.
Ratkaisu:
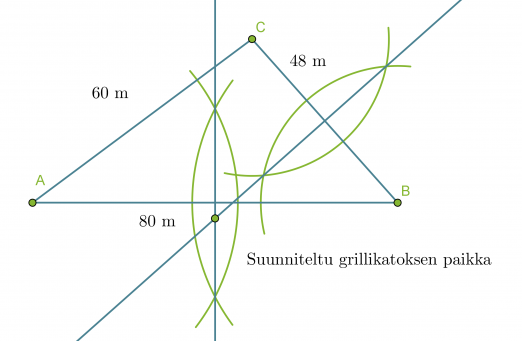
Merkitään piirroksessa taloja kirjaimilla A, B ja C. Piirretään aluksi jana AB, jonka kuvaa pituutta 80 m. Talon C sijainti määritetään harpin avulla käyttäen pisteitä A ja B ympyräkaarien keskipisteinä, jonka säteiden pituudet ovat 60 m ja 48 m.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
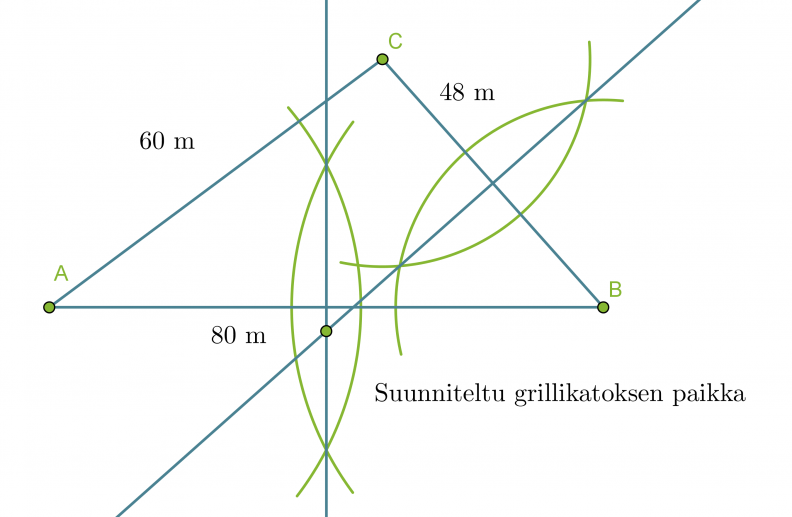
Jotta grillipaikka olisi yhtä kaukana taloista A ja B on sen oltava janan AB keskinormaalilla. Vastaavasti, jotta se olisi yhtä kaukana taloista B ja C, on grillikatoksen sijaittava janan BC keskinormaalilla. Keskinormaalien leikkauspisteestä löytyy paikka, joka on yhtä kaukana kaikista taloista.
Huom! Vastauksen voi tarkistaa piirtämällä keskinormaalin myös janalle AC. Jotta vastaus olisi oikein, tulee janan AC keskinormaalin leikata muiden sivujen keskinormaalit samassa pisteessä.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014