2. Monikulmiot
Suljettua murtoviivan rajoittamaa tasoaluetta sanotaan monikulmioksi ja murtoviivaa monikulmion piiriksi. Jos monikulmiossa kaikki sivut ovat yhtä pitkiä ja kaikki kulmat yhtä suuria, on monikulmio säännöllinen. Monikulmion pinta-alan laskeminen vaatii usein monikulmion jakamista osiin. Säännölliset monikulmiot voidaan jakaa tasakylkisiin keskuskolmioihin, jotka ovat yhteneviä.
Monikulmio nimetään siinä olevien kulmien, kärkien tai sivujen mukaan. Yleisesti n-kulmiolla on n kulmaa, n kärkeä ja n sivua.
n-kulmion kulmien summa on (n-2) · 180°.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
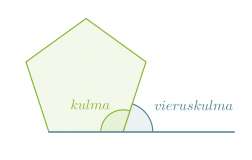
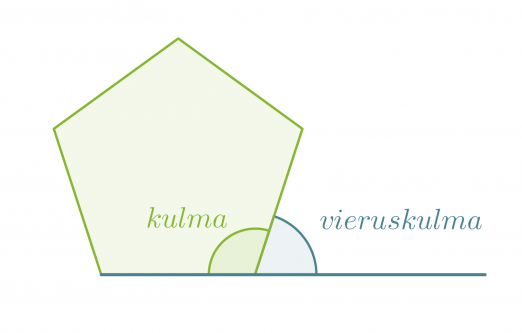
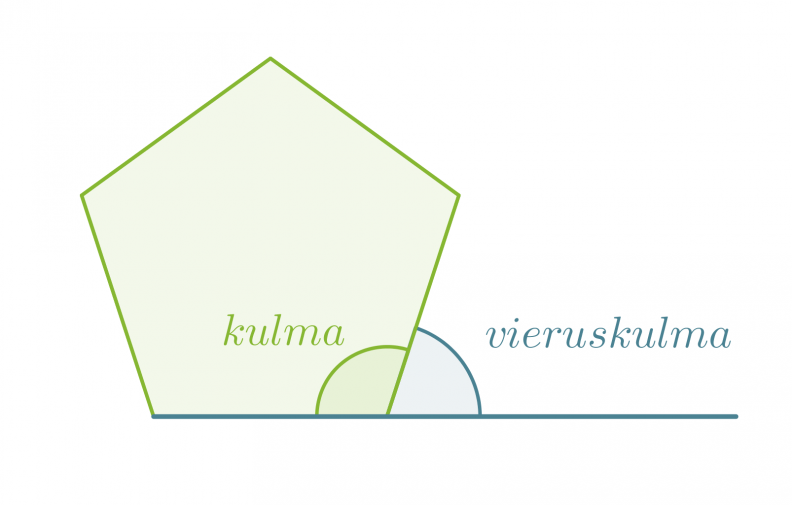
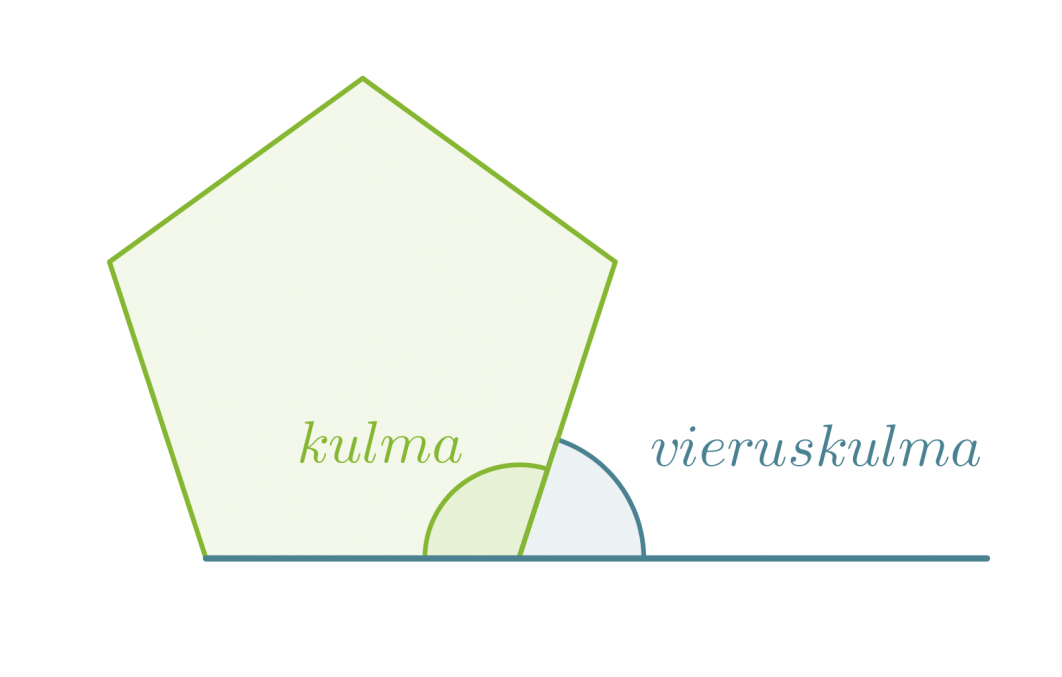
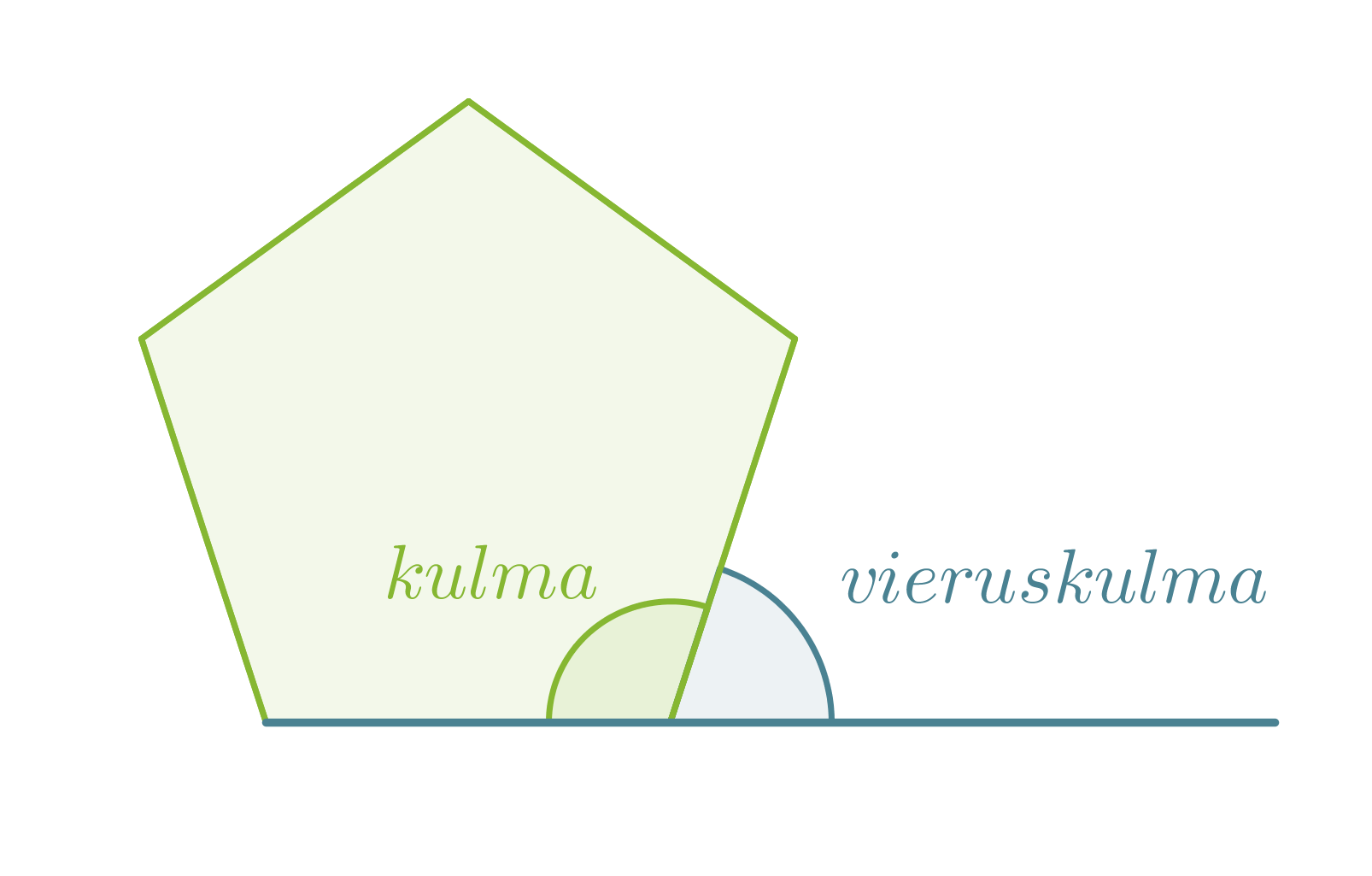
Monikulmion kulman ja sitä vastaavan vieruskulman summa on aina 180°. Kaikkien monikulmion vieruskulmien summa on puolestaan 360°.
Säännöllisen n-kulmion kulman vieruskulman suuruus on
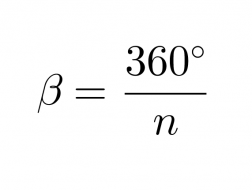
Klikkaa kuva suuremmaksi!
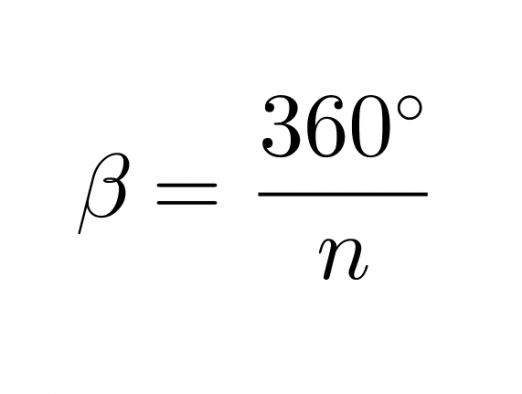
Klikkaa kuva suuremmaksi!
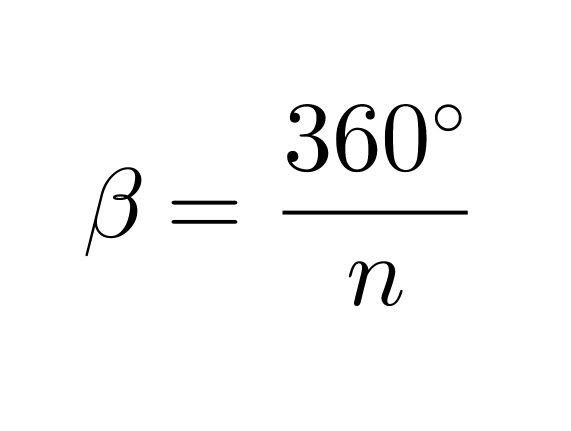
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Säännölliset monikulmiot ovat yhdenmuotoisia keskenään: kaikki tasasivuiset kolmiot ovat siis keskenään yhdenmuotoisia, kaikki neliöt ovat keskenään yhdenmuotoisia jne.
Yhdenmuotoisten kuvioiden pinta-alojen suhde on verrannollinen pituuksien suhteiden neliöön.
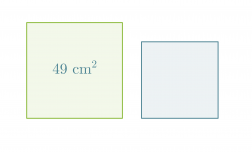
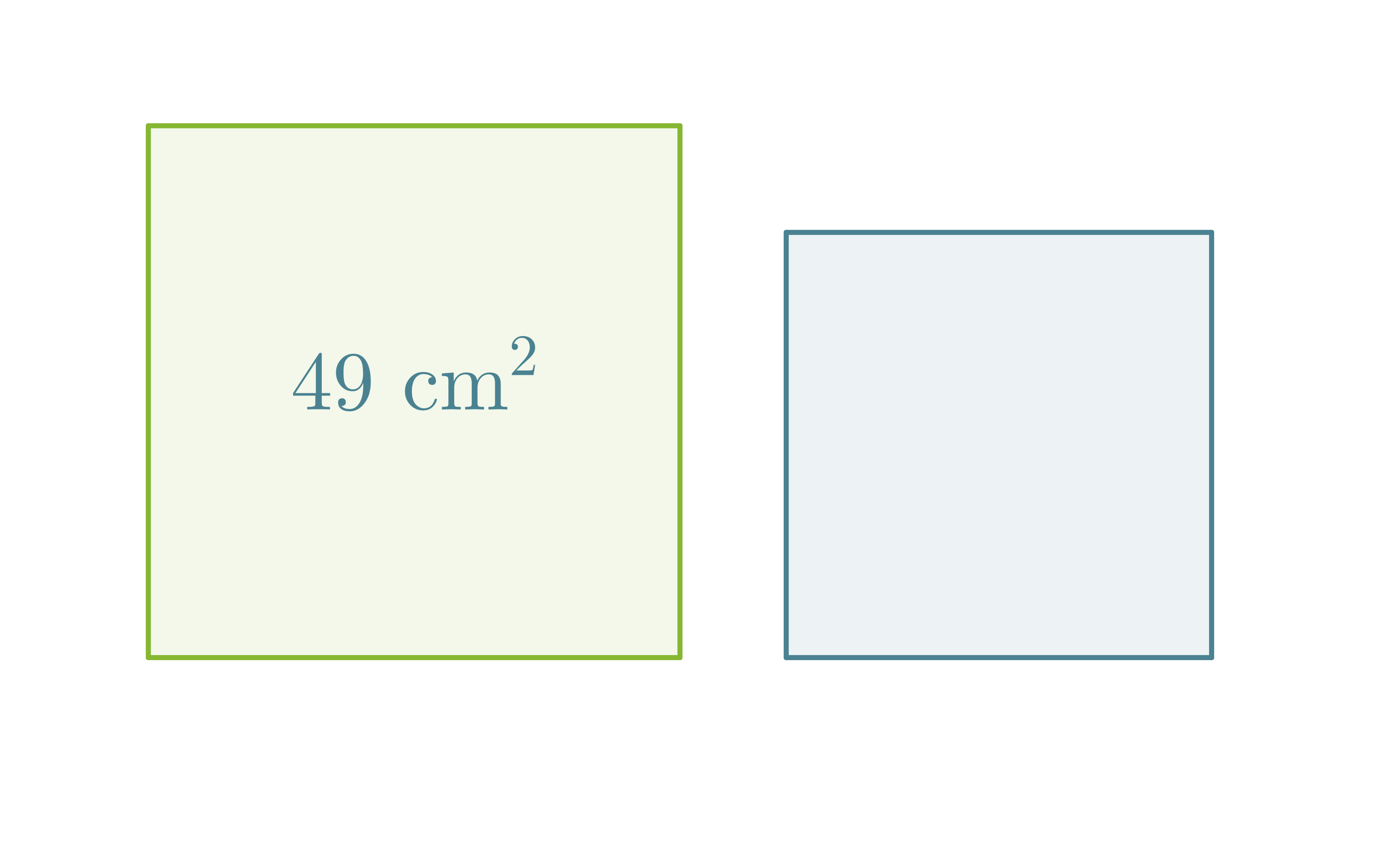
Esimerkki 1.
Mikä on pienemmän neliön pinta-ala, kun neliöiden sivujen pituuksien suhde on 5 : 4?
Klikkaa kuva suuremmaksi!
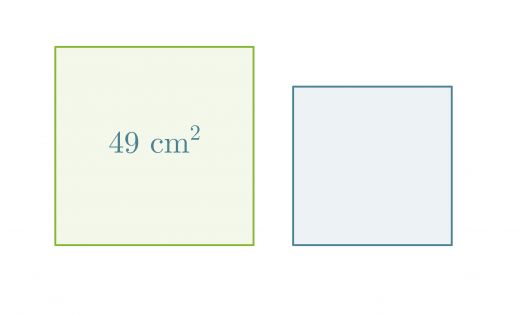
Klikkaa kuva suuremmaksi!
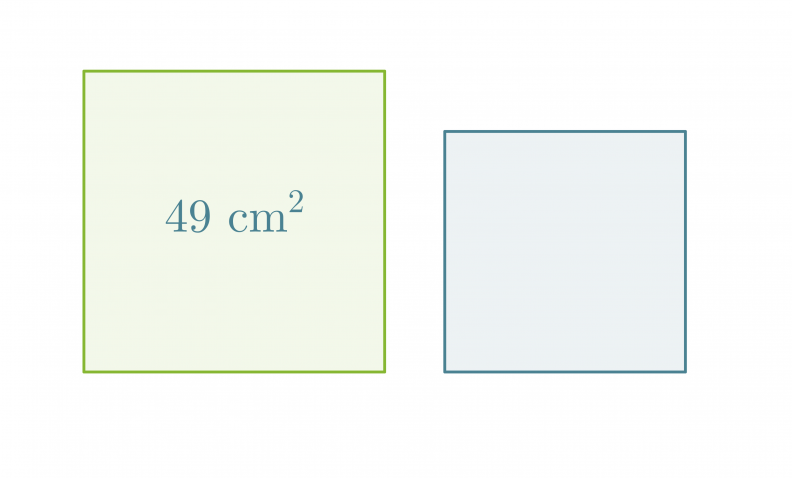
Klikkaa kuva suuremmaksi!
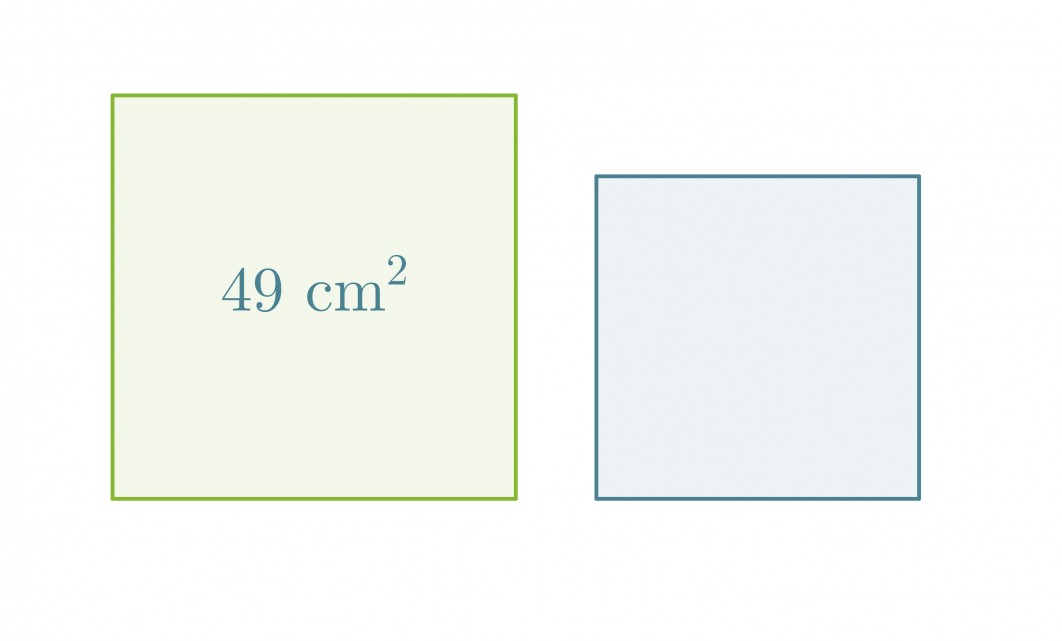
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
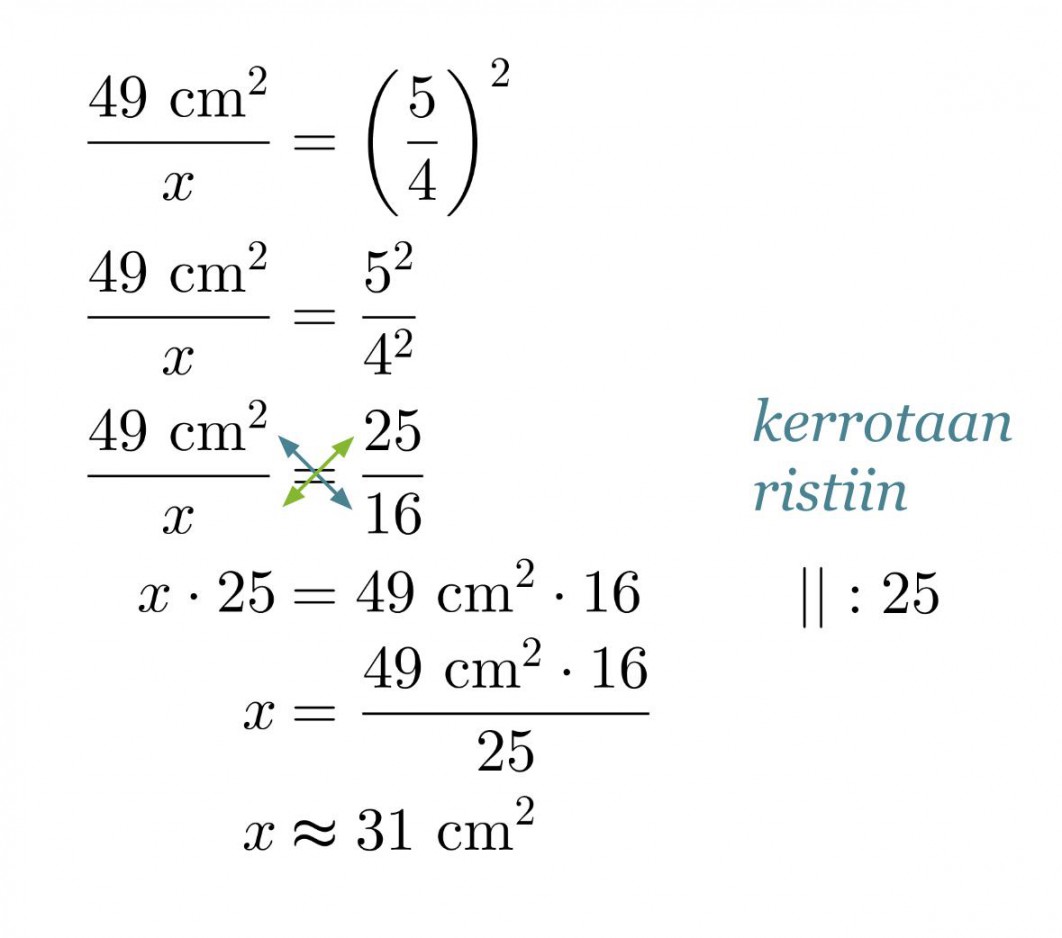
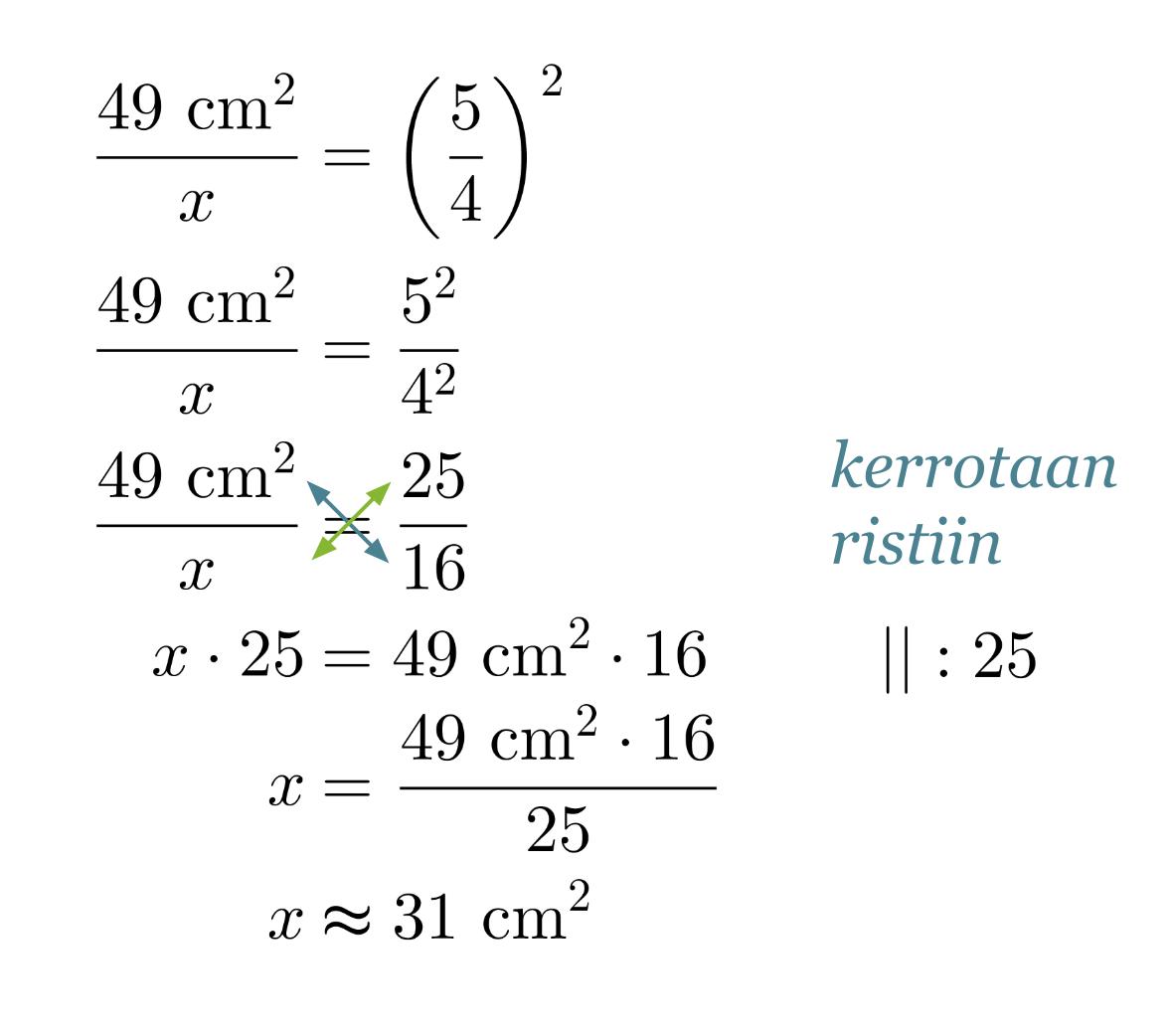
Merkitään pienemmän neliön pinta-alaa x:llä. Kaikki neliöt ovat keskenään yhdenmuotoisia, jolloin niiden pinta-alojen suhde on verrannollinen pituuksien suhteiden neliöön.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Pienemmän neliön pinta-ala on noin 31 cm2.
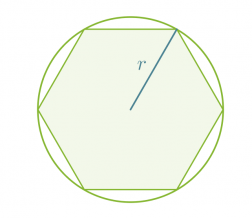
Säännöllisellä monikulmiolla on keskipiste, joka on yhtä kaukana monikulmion kärjistä ja yhtä kaukana sivuista. Säännöllisen monikulmion ympäri ja sisään voidaan piirtää ympyrä käyttäen keskipisteenä monikulmion keskipistettä. Säännölliset monikulmiot voidaan piirtää hyödyntämällä ympyräsektoreita, joiden säde on keskipisteen etäisyys monikulmion kärjestä tai sivusta.
Klikkaa kuva suuremmaksi!
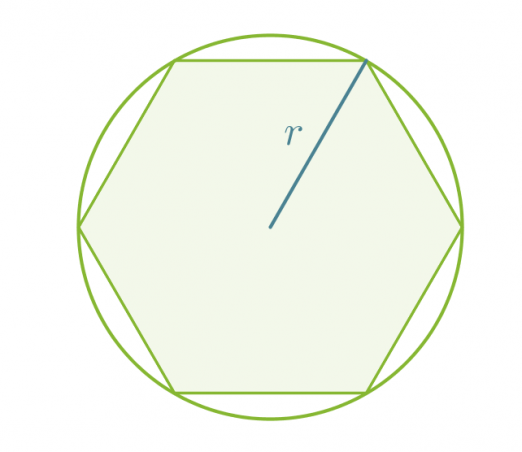
Klikkaa kuva suuremmaksi!
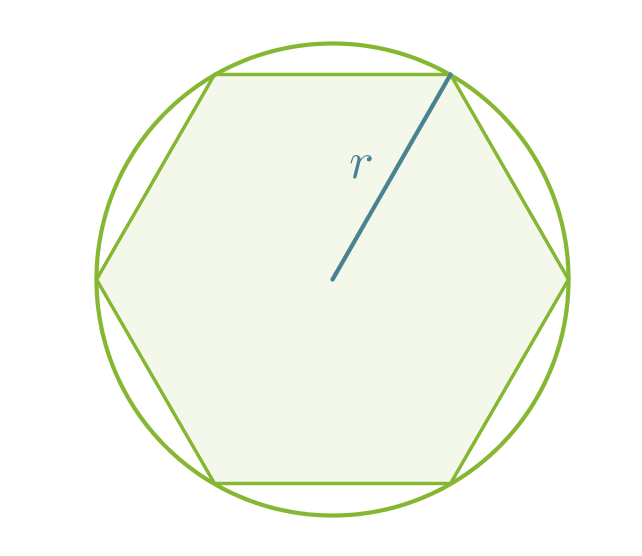
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jokainen säännöllisen monikulmion kärki sijaitsee ympyrän kehällä.
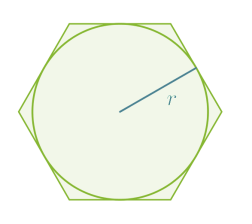
Klikkaa kuva suuremmaksi!
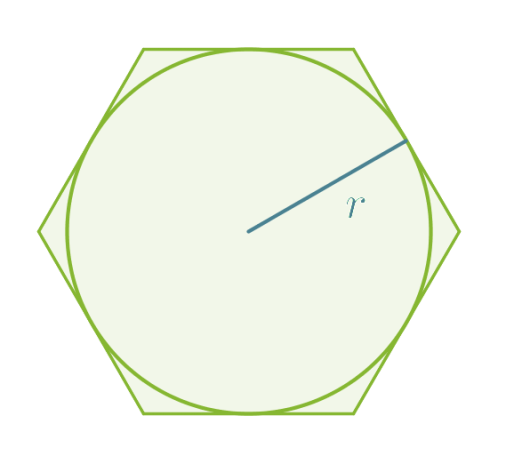
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jokainen säännöllisen monikulmion sivu sivuaa eli koskettaa ympyrän kehää.
Esimerkki 2.
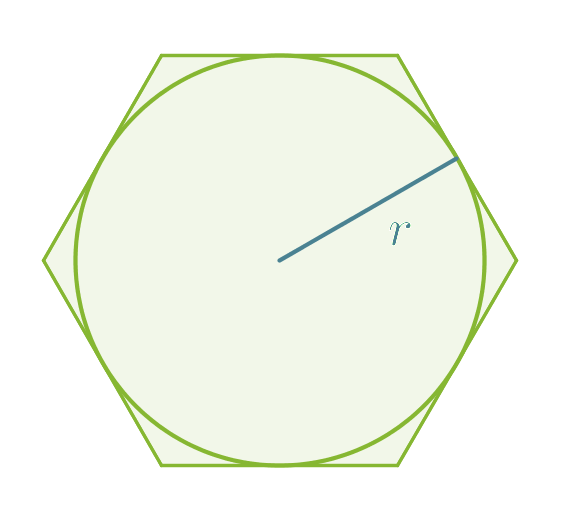
Piirretään säännöllinen kahdeksankulmio.
Säännöllisen monikulmion vieruskulma b saadaan lasketuksi, kun tiedetään sivujen lukumäärä.
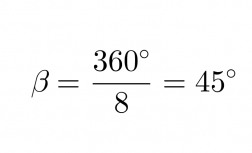
Klikkaa kuva suuremmaksi!
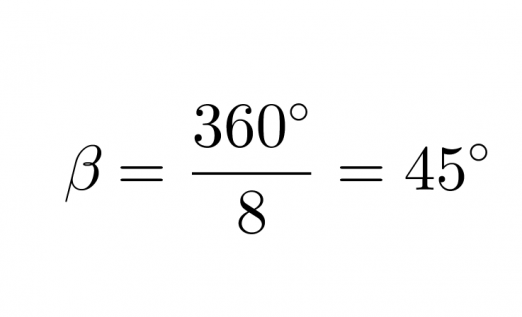
Klikkaa kuva suuremmaksi!
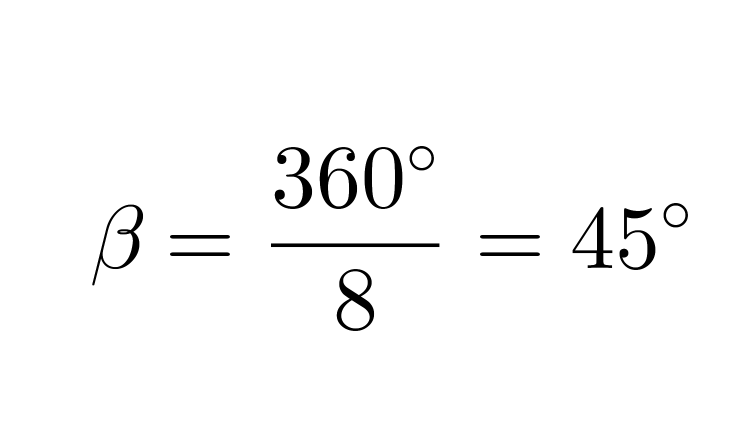
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jaetaan ympyrä vieruskulman suuruisiin sektoreihin.
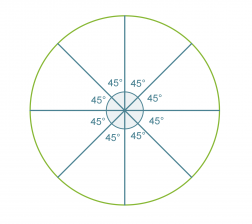
Klikkaa kuva suuremmaksi!
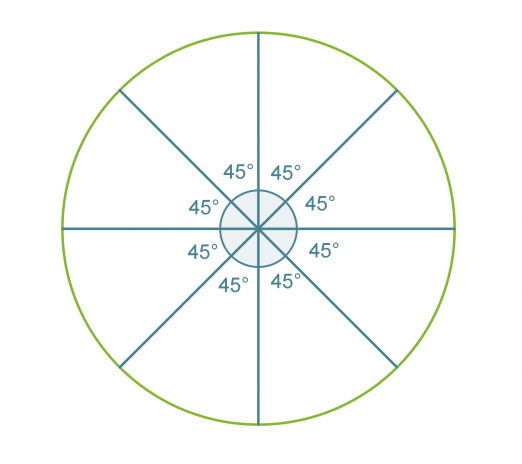
Klikkaa kuva suuremmaksi!
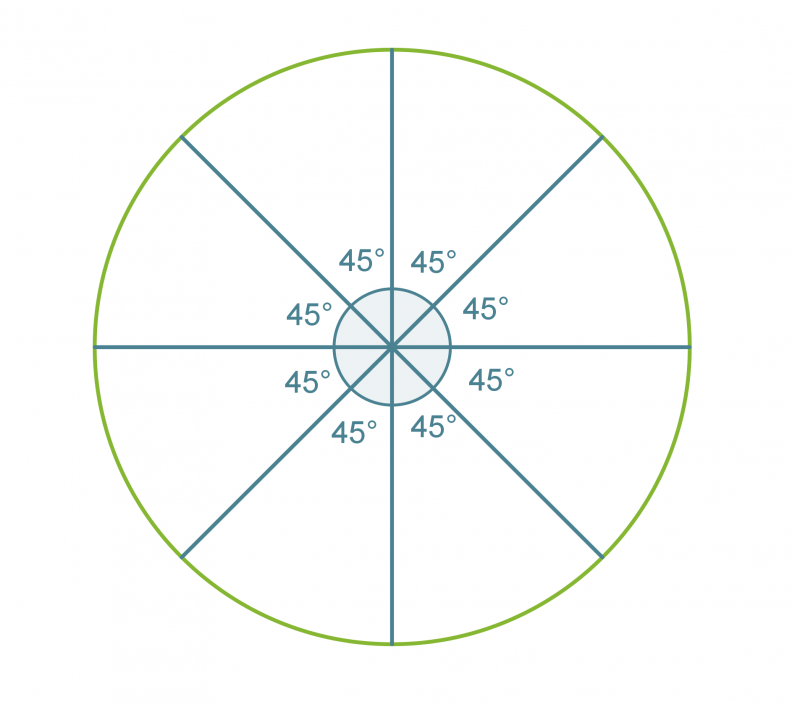
Klikkaa kuva suuremmaksi!
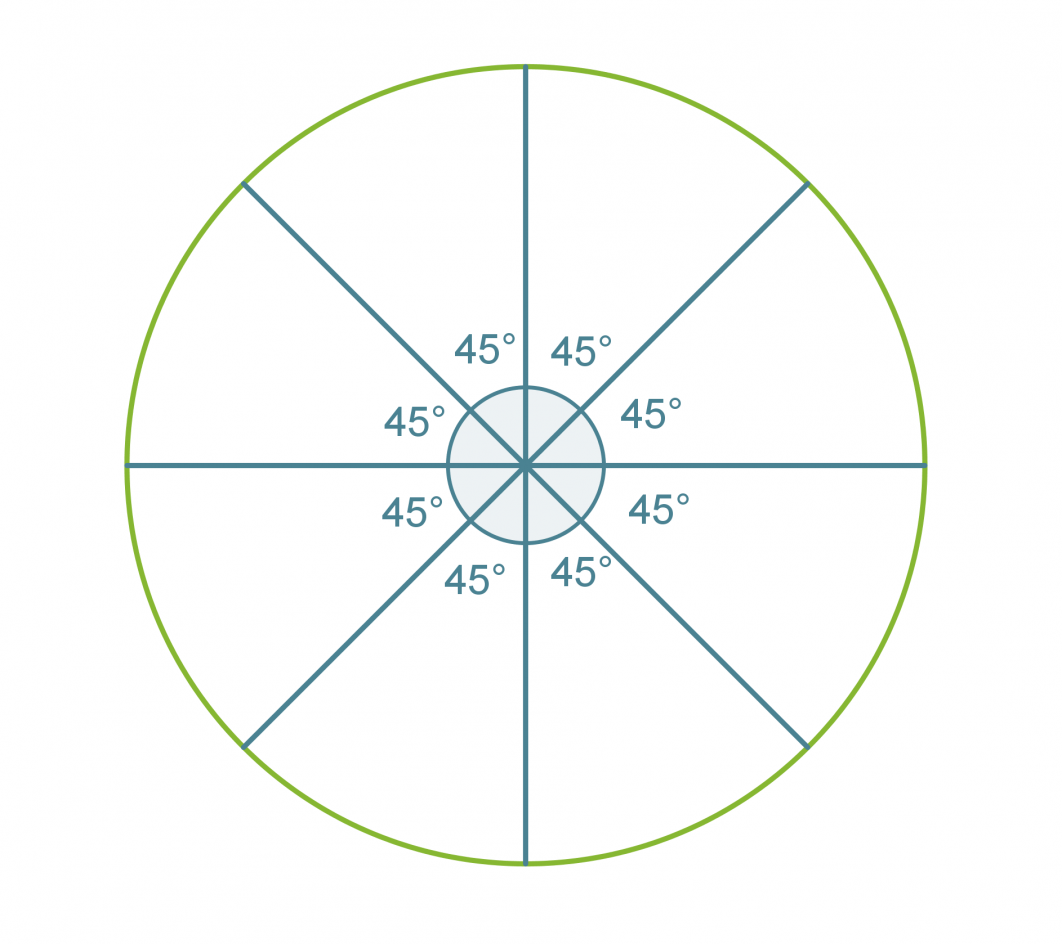
Klikkaa kuva suuremmaksi!
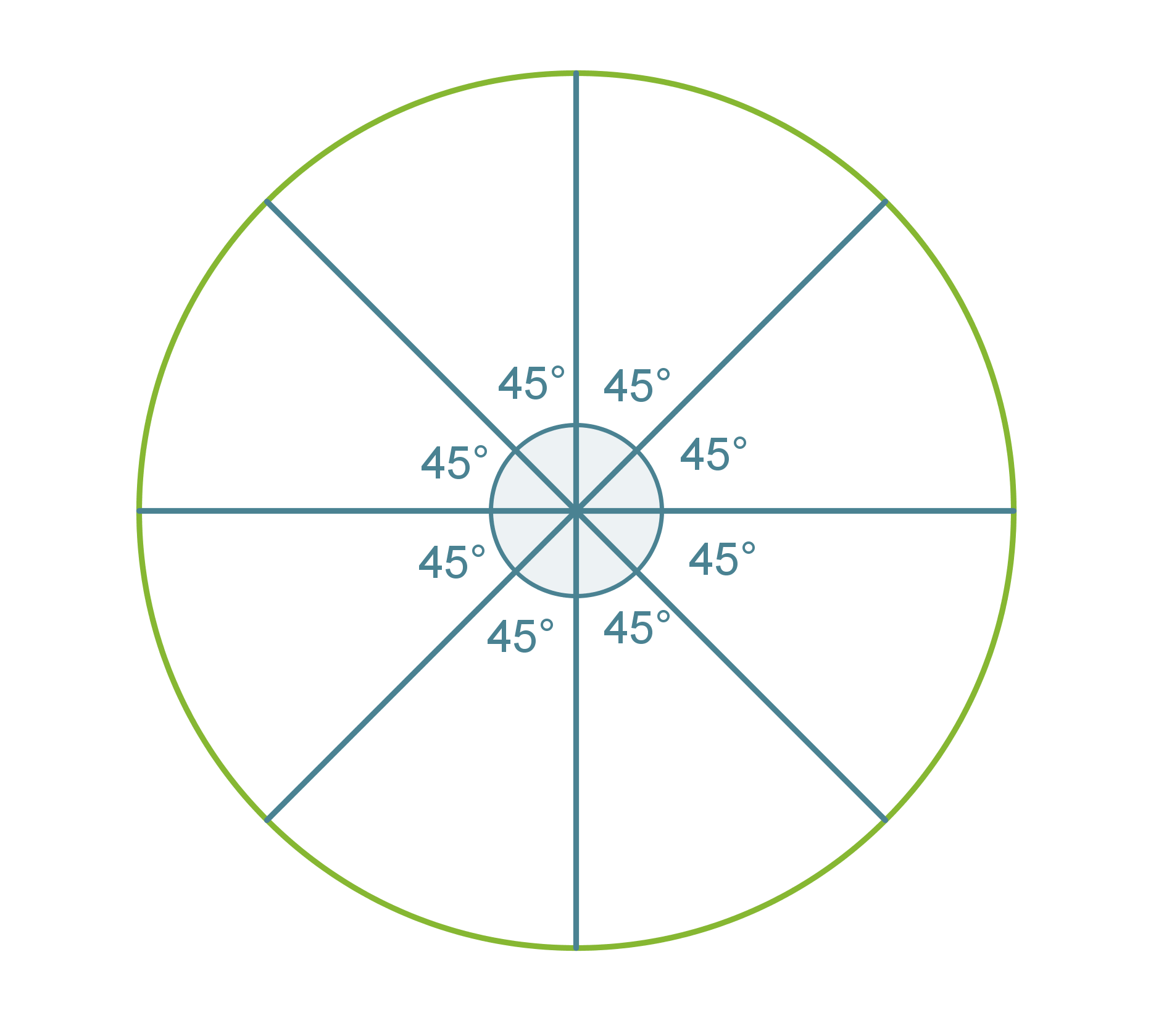
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
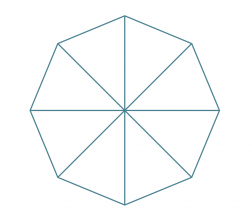
Klikkaa kuva suuremmaksi!
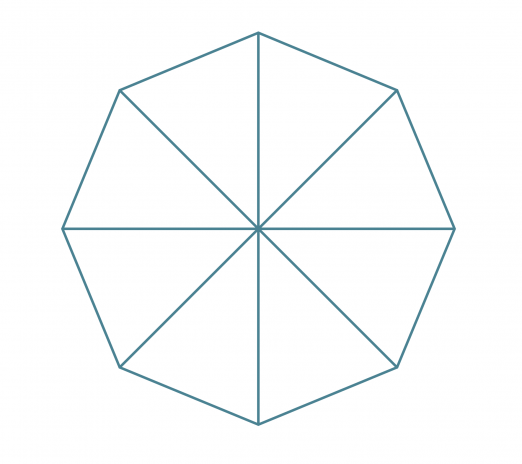
Klikkaa kuva suuremmaksi!
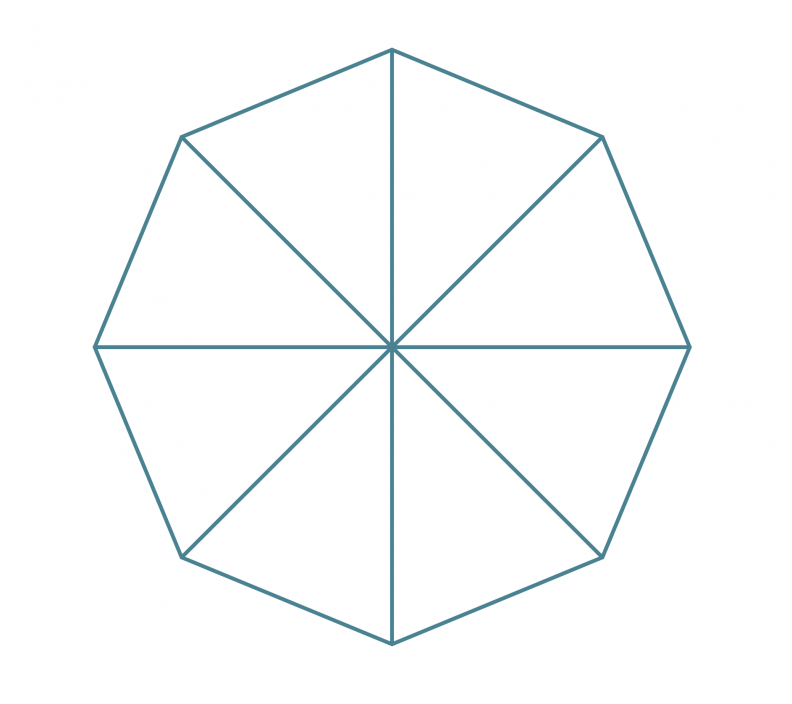
Klikkaa kuva suuremmaksi!
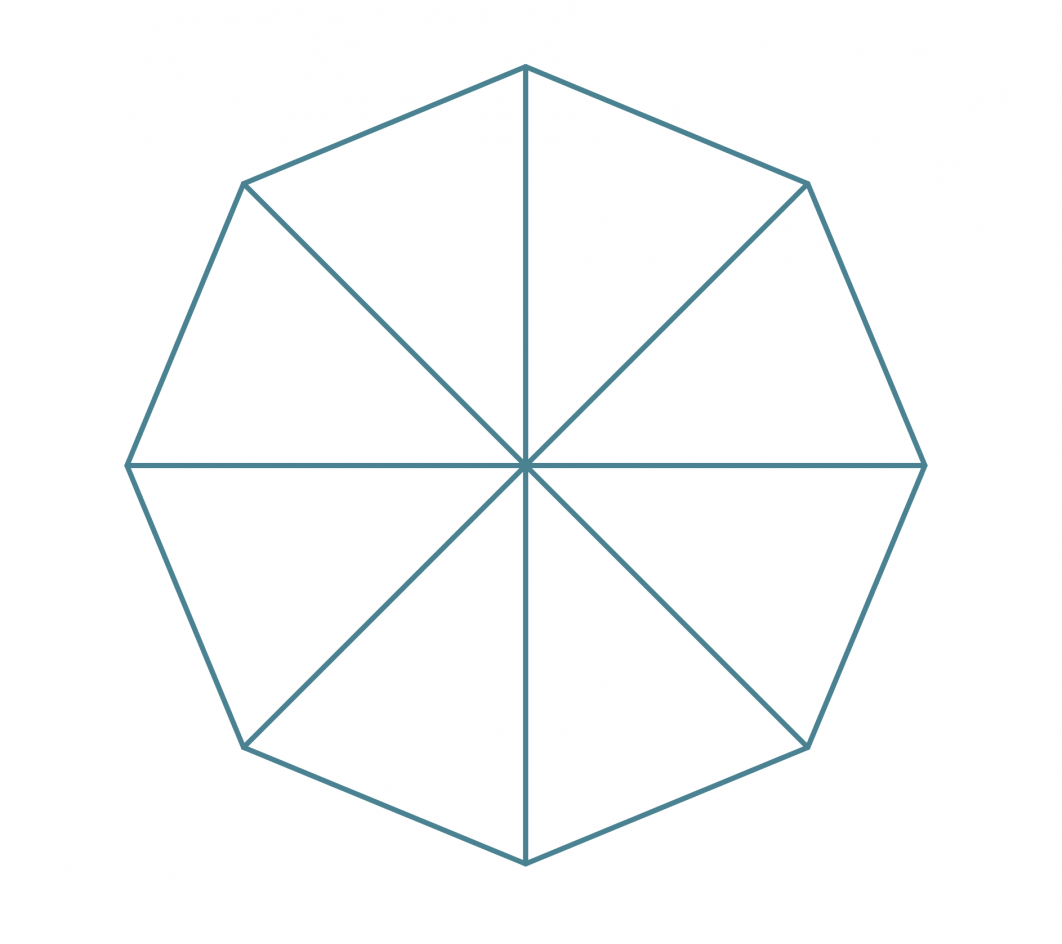
Klikkaa kuva suuremmaksi!
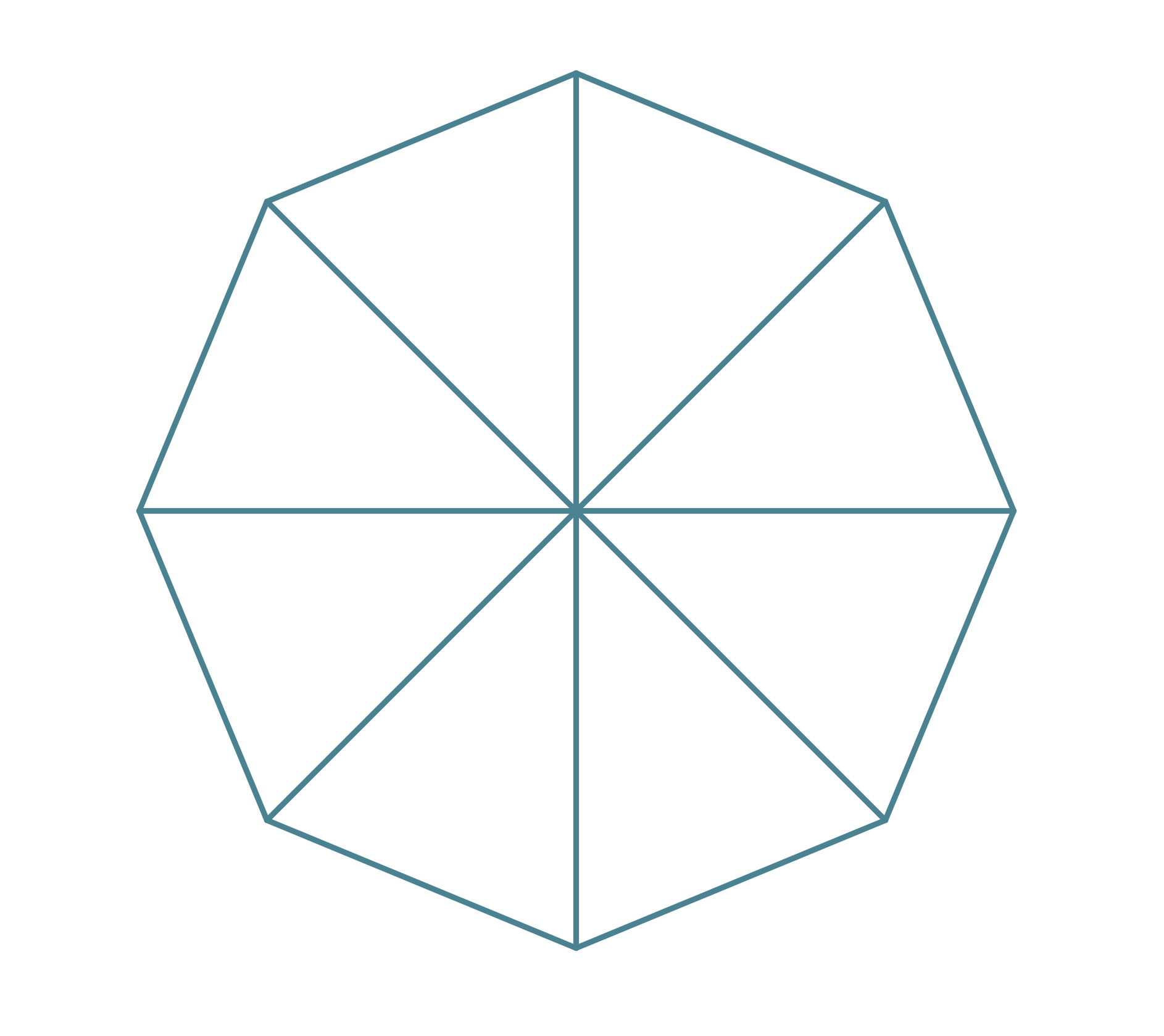
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yhdistetään säteet.
“Monikulmioista yksinkertaisin on kolmio.”
Säännöllisen monikulmion piirtäminen