3. Tangentti
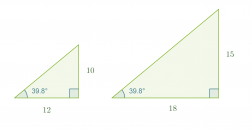
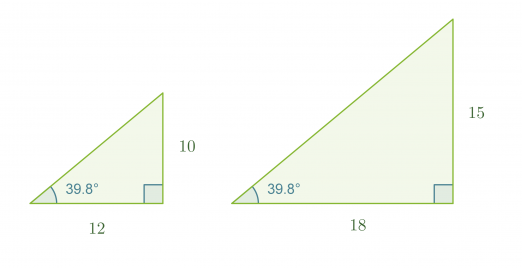
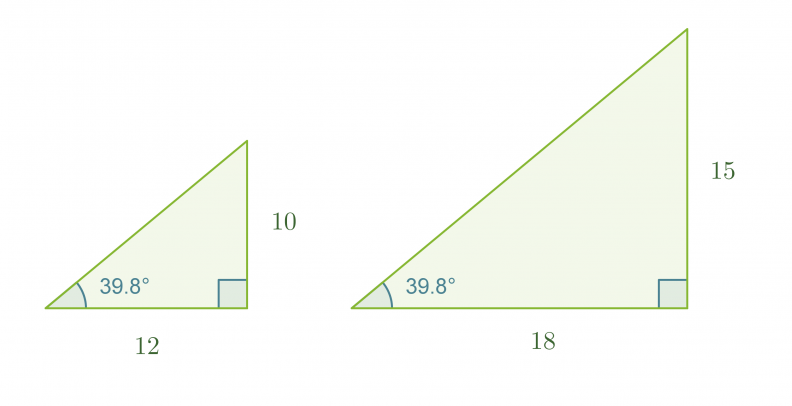
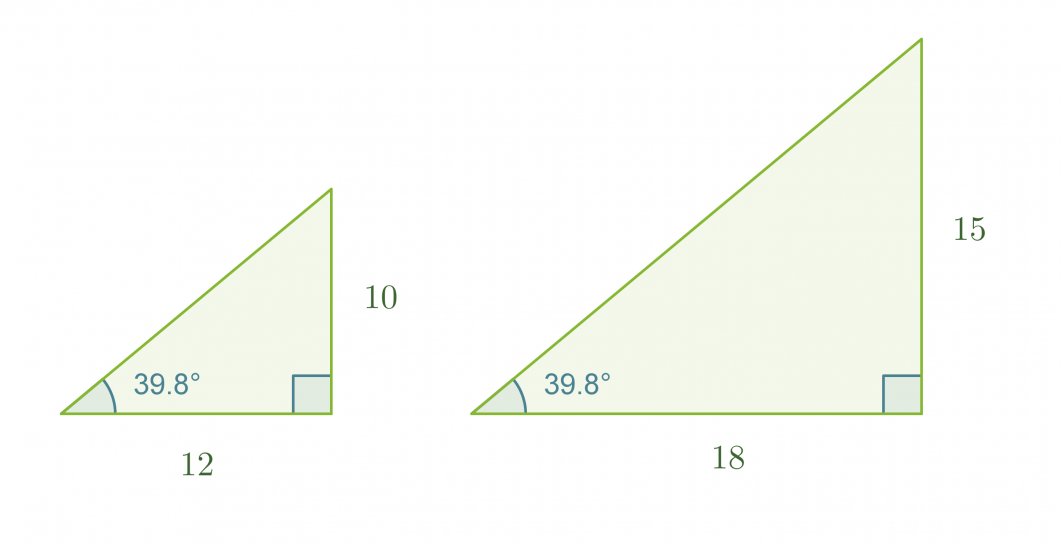
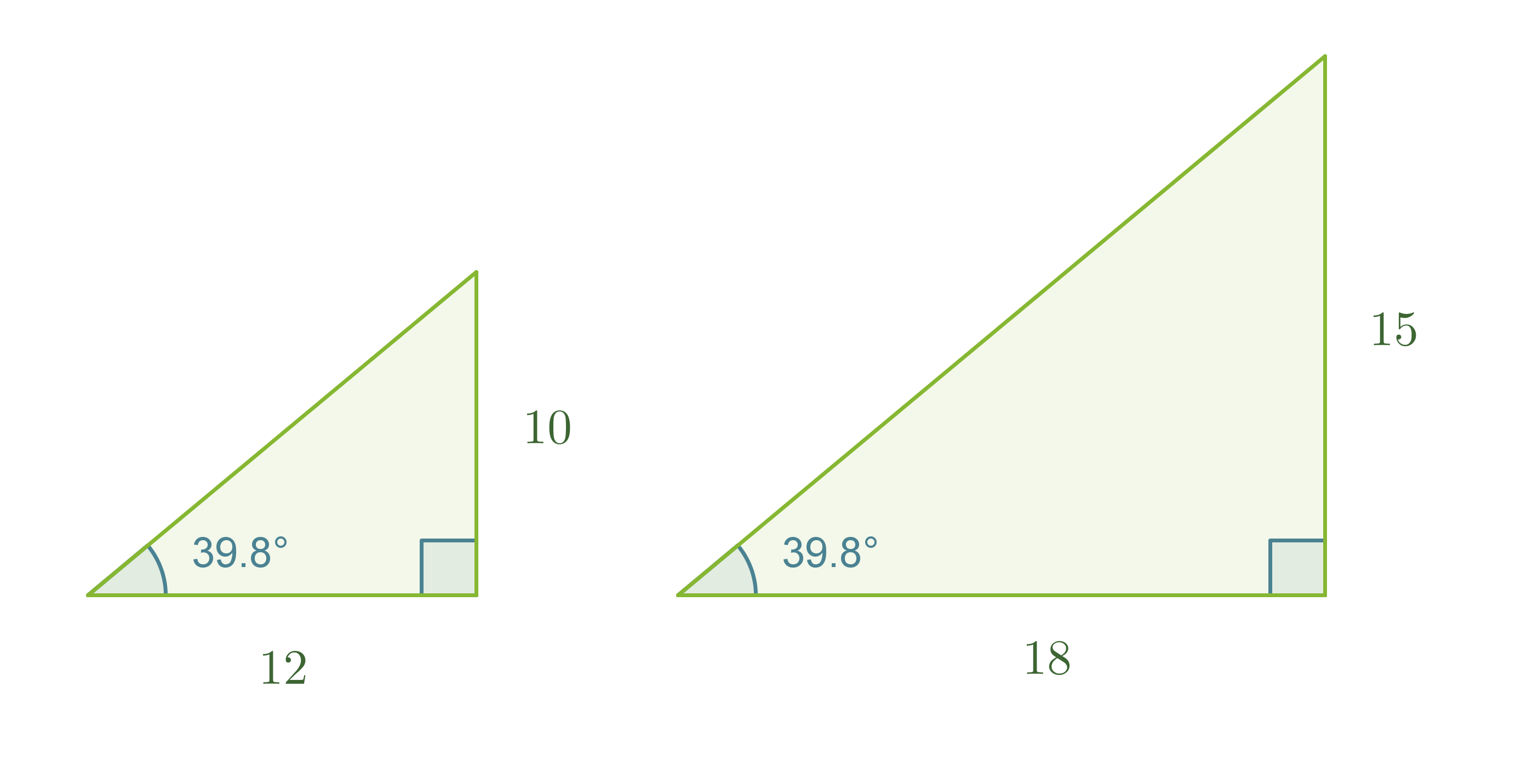
Tarkastellaan kahta suorakulmaista kolmiota, joiden molempien toinen terävä kulma on 39,8˚. Kolmiot ovat yhdenmuotoisia, koska molempien kolmioiden kolmannetkin kulmat ovat yhtä suuria.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yhdenmuotoisien kolmioiden vastinsivujen suhteet ovat samat, jolloin voidaan muodostaa verranto
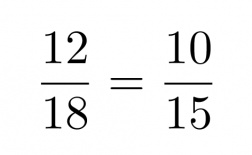
Klikkaa kuva suuremmaksi!
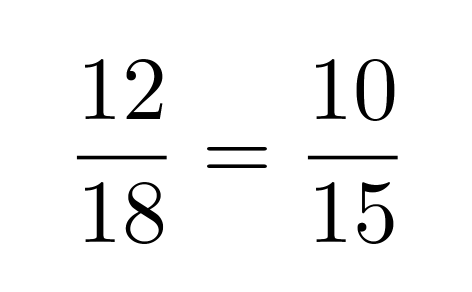
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suoritetaan verrannolle ristiin kertominen ja muutetaan se toiseen muotoon.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tässä muodossa ilmaistu verranto tarkoittaa, että kulman 39,8˚ vastaisen kateetin suhde viereiseen kateettiin on vakio. Suhteet 10/12 ja 15/18 ovat muodostuneet ainoastaan yhden kolmion sivujen pituuksista. Näitä suhteita kutsutaan kulman 39,8˚ tangentiksi.
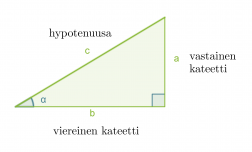
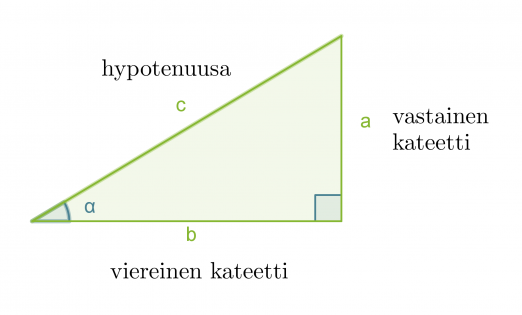
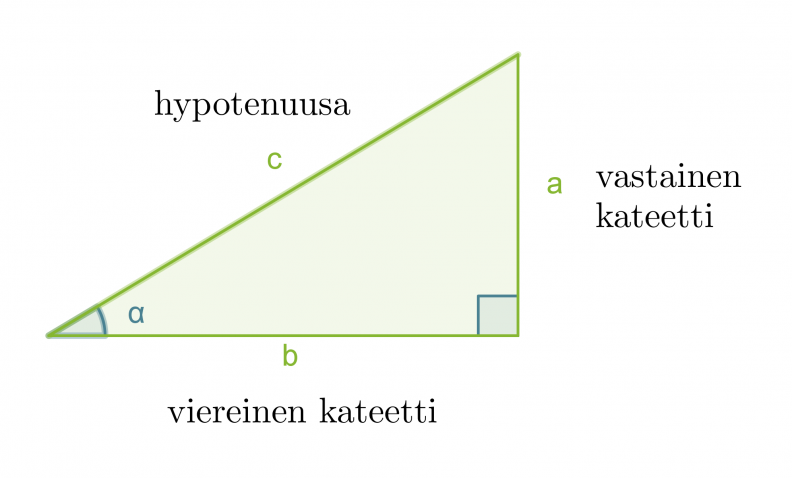
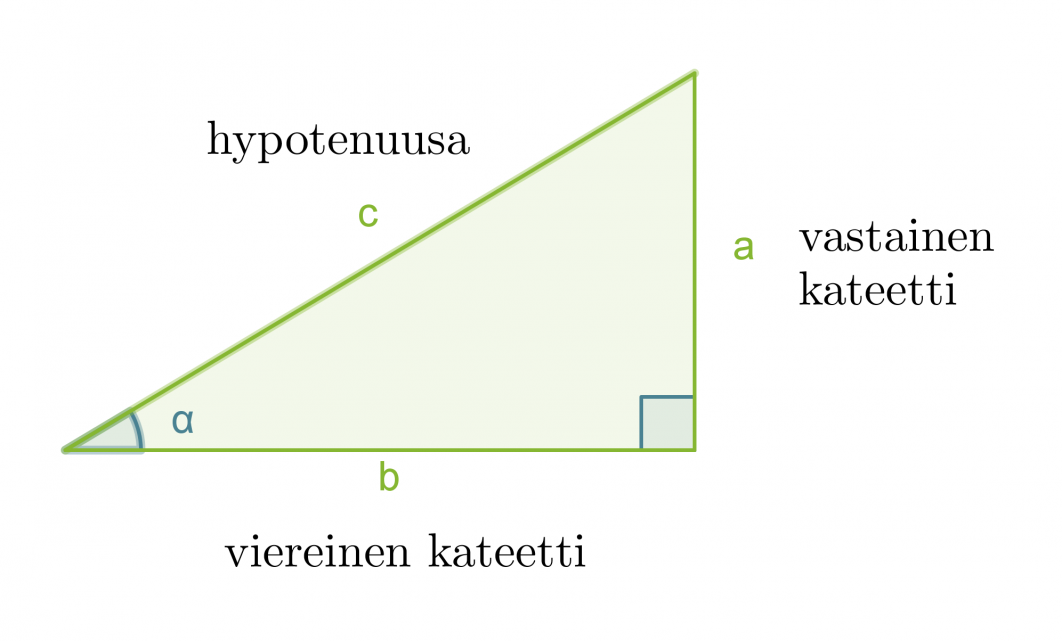
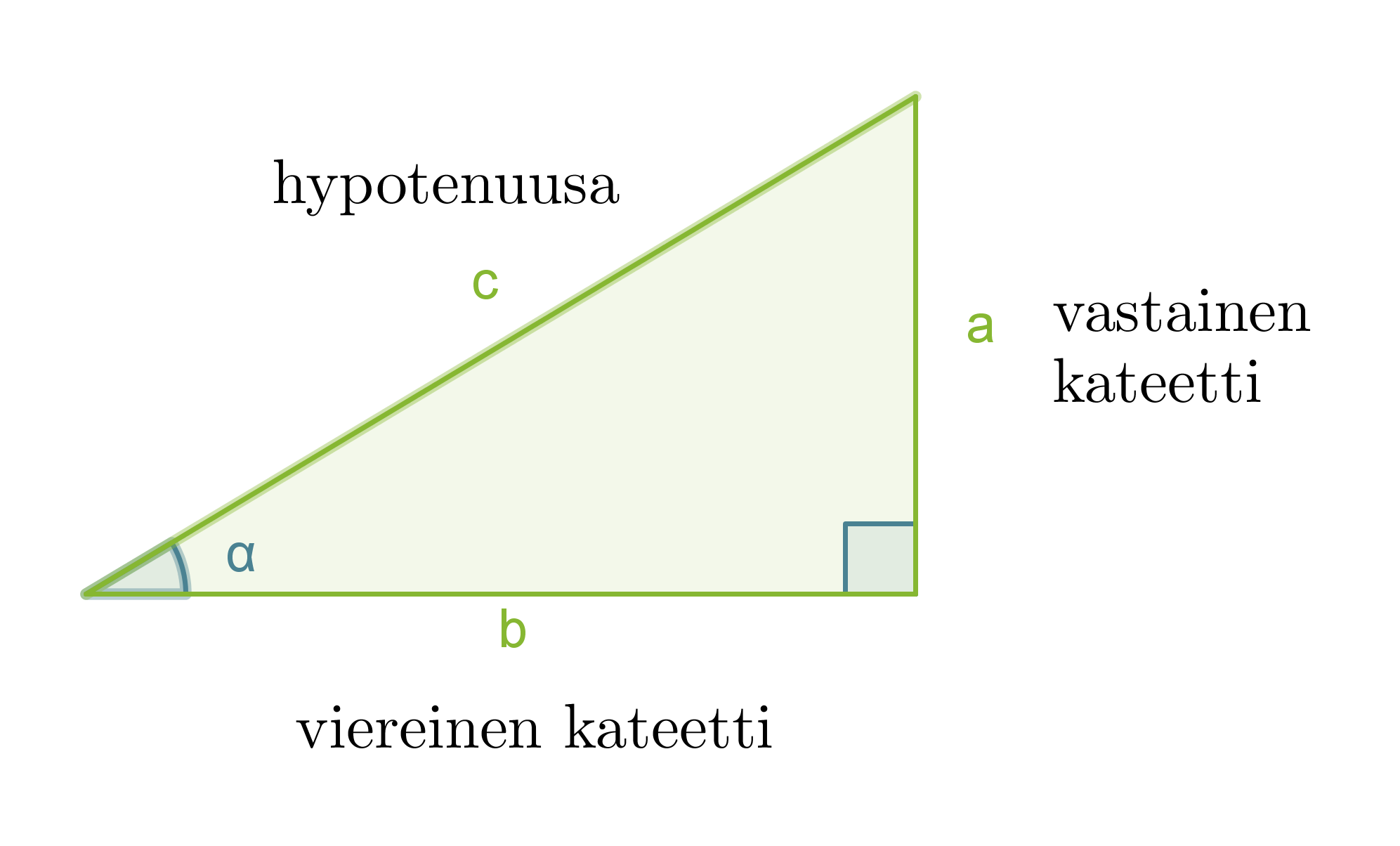
Suorakulmaisessa kolmiossa terävän kulman α tangentti on kulman vastaisen kateetin suhde kulman viereiseen kateettiin.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
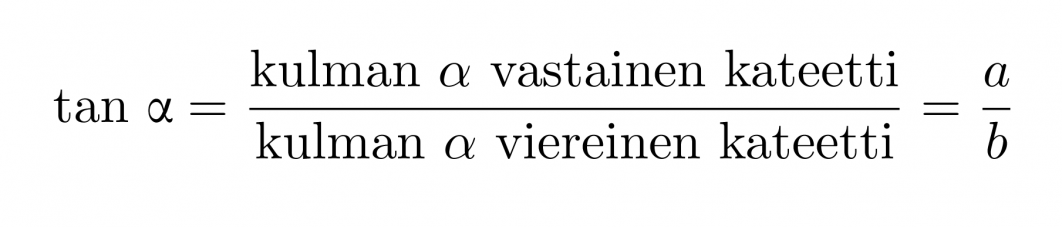
Klikkaa kuva suuremmaksi!
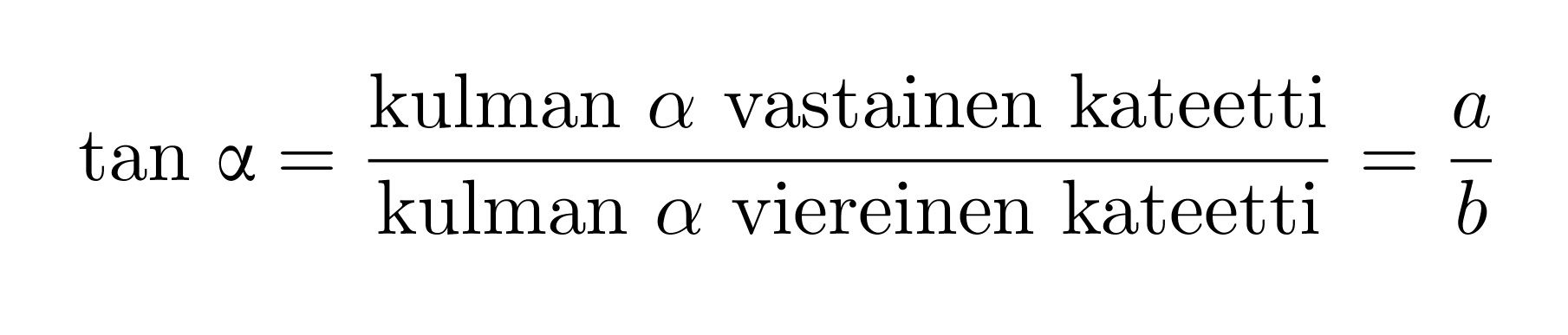
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
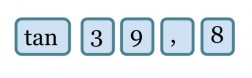
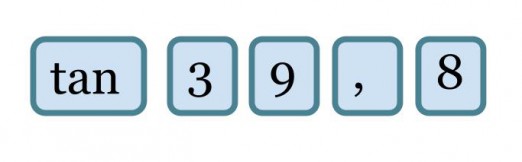
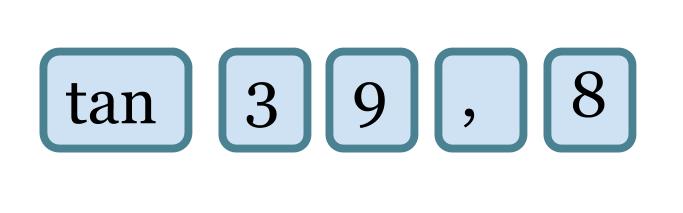
Trigonometria perustuu suorakulmaisten kolmioiden yhdenmuotoisuuteen. Trigonometristen funktioiden arvoja on valmiiksi taulukoituna, mutta ne saadaan myös laskettua kätevästi funktiolaskimilla. Jos laskimeen näppäillään
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
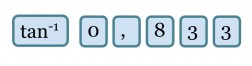
saadaan tulokseksi noin 0,833 eli sama tulos kuin jakolaskusta 10 : 12 tai 15 : 18. Trigonometristen funktioiden käyttö usein helpottaa suorakulmaisiin kolmioihin liittyviä laskuja, koska sivujen suhteita voidaan välittömästi käyttää hyväksi, kun toinen suorakulmaisen kolmion terävistä kulmista tunnetaan.
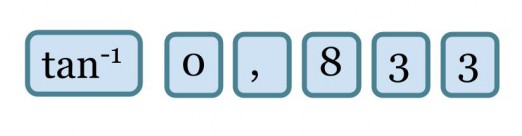
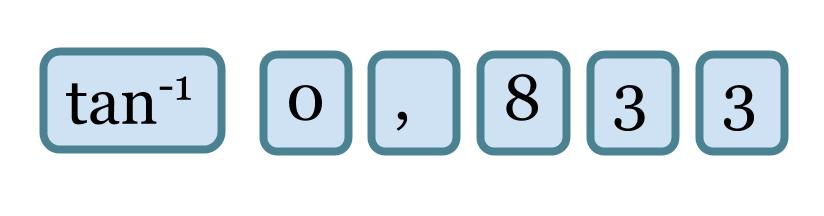
Vastaavasti, jos suorakulmaisen kolmion molempien kateettien pituudet tunnetaan, voidaan niiden verrannon avulla määrittää kolmion terävät kulmat. Laskimella otetaan silloin kateettien pituuksien suhteesta tangentin käänteistoiminto, joka antaa tulokseksi kulman suuruuden asteina.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1
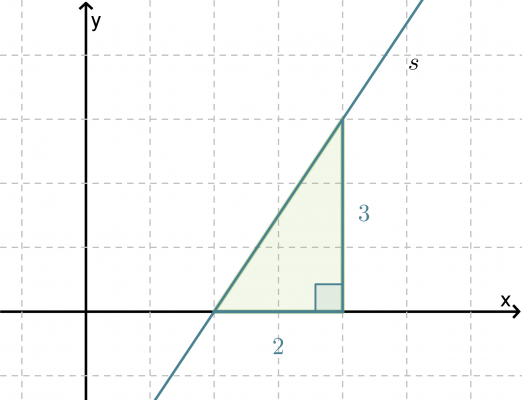
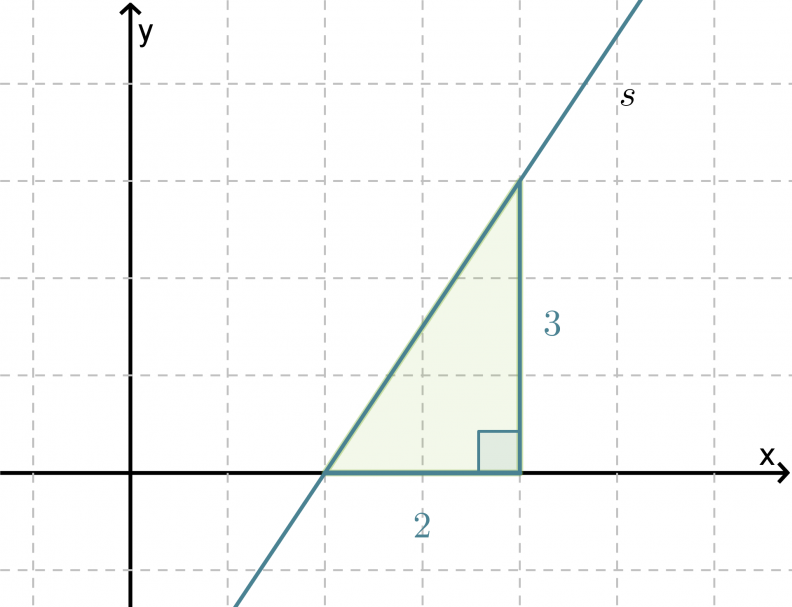
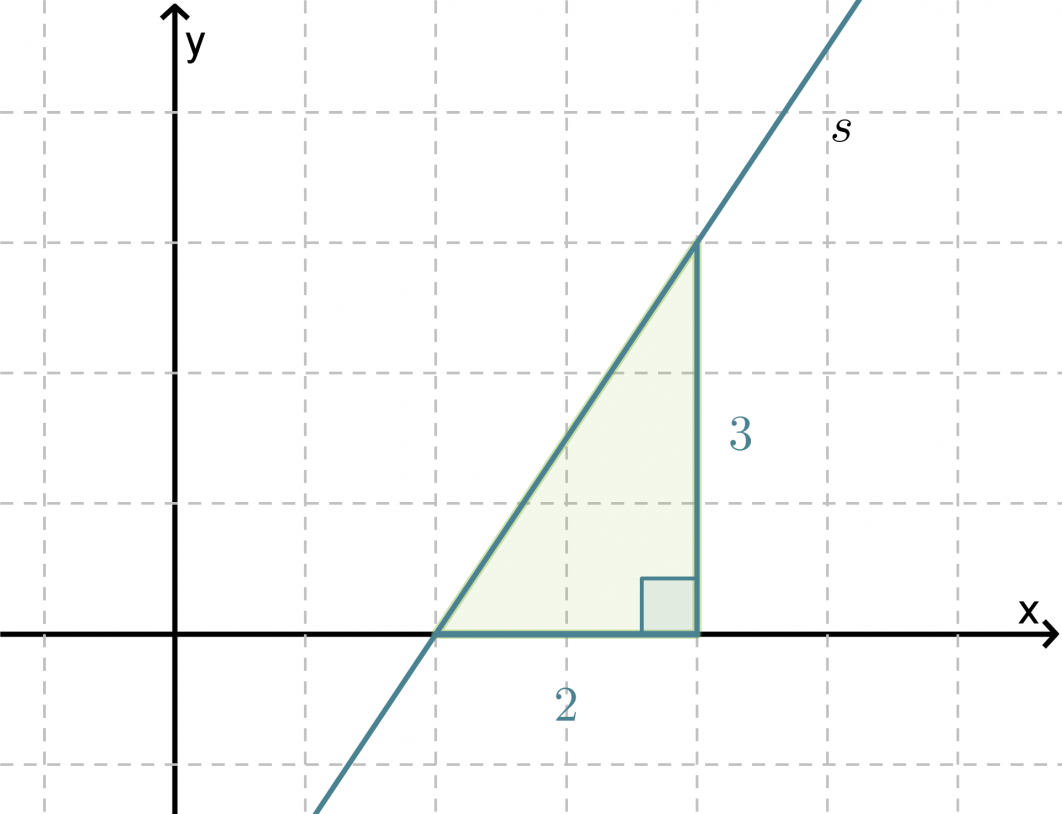
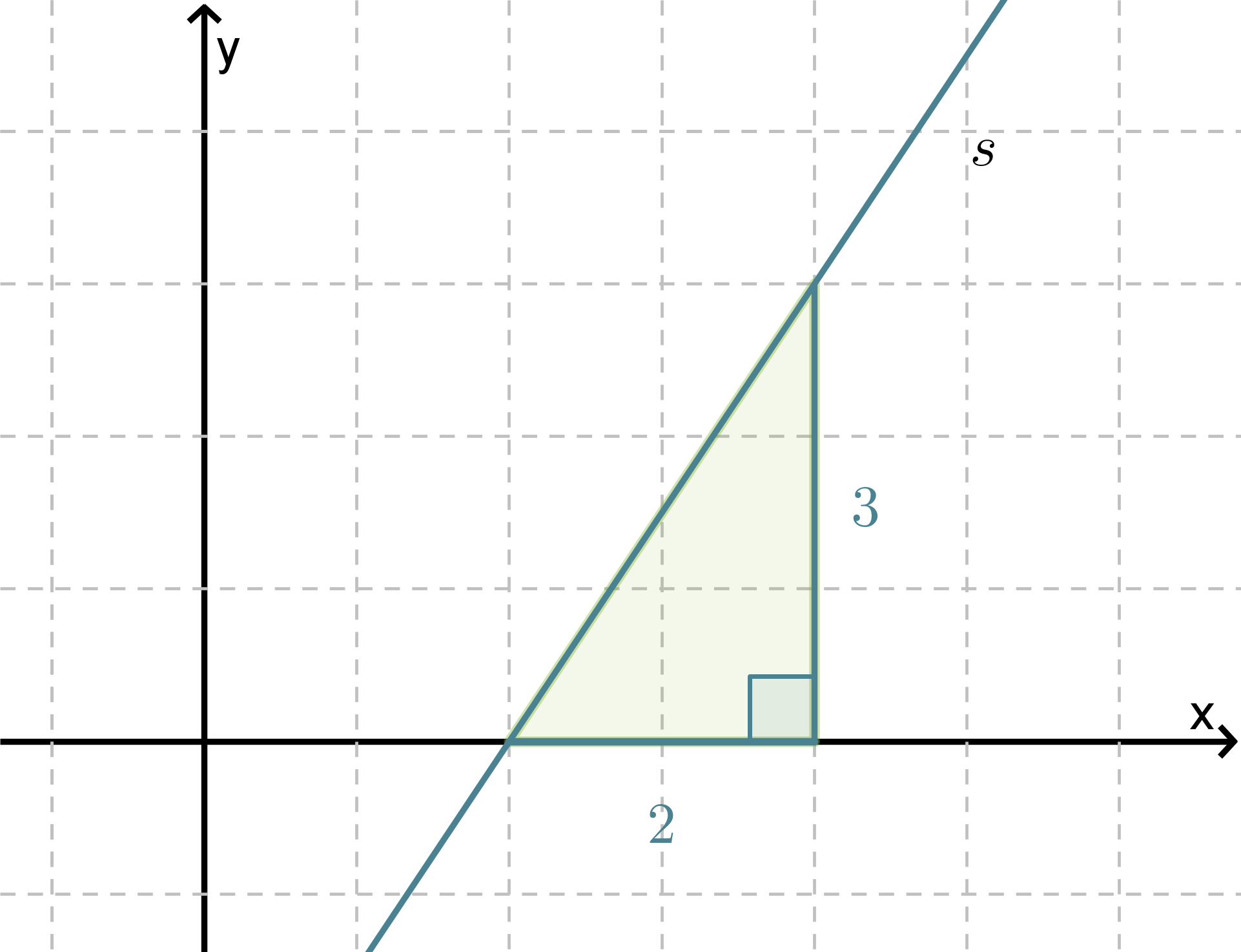
Lasketaan, kuinka suuren kulman suora s muodostaa x-akselin kanssa. Kyseistä kulmaa sanotaan suoran suuntakulmaksi.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
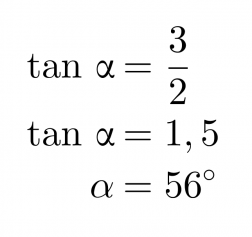
Klikkaa kuva suuremmaksi!
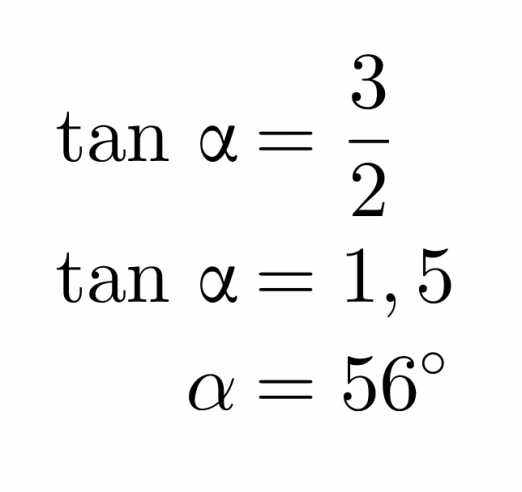
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
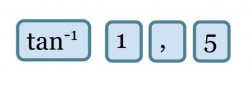
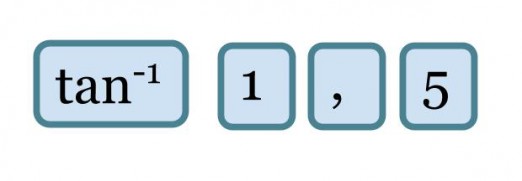
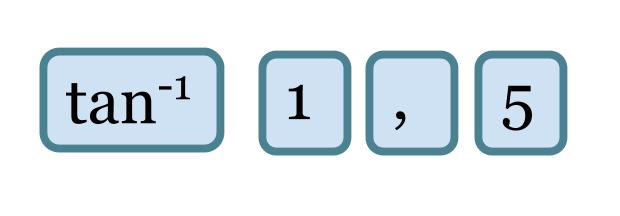
Kulma α saadaan selville näppäilemällä laskimeen
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Kulman suuruus on 56°.
Esimerkki 2.
Lasketaan kuvassa olevan puun korkeus.
Tangentin määritelmän mukaan voidaan kirjoittaa yhtälö
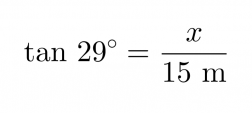
Klikkaa kuva suuremmaksi!
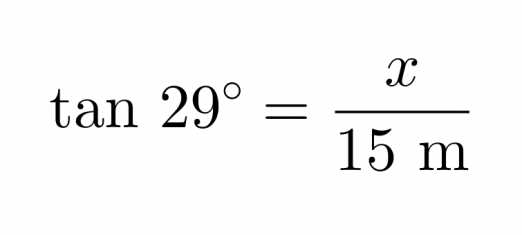
Klikkaa kuva suuremmaksi!
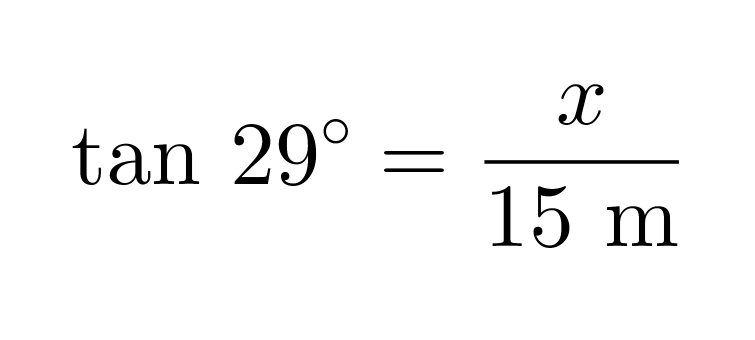
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
joka ratkaistaan seuraavasti:

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
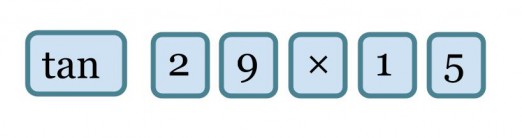
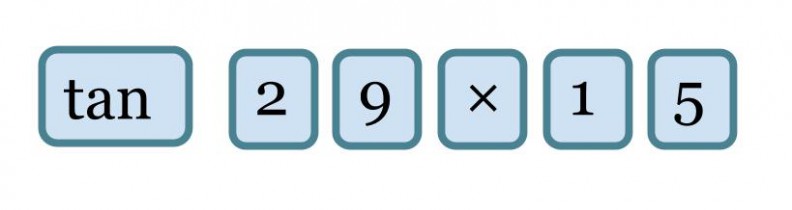
Kateetin x pituus saadaan lasketuksi näppäilemällä laskimeen

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Puun korkeus on 8,3 m.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014