5. Pythagoraan lause ja *muistikolmiot
Pythagoraan lause
Suorakulmaisessa kolmiossa kateettien neliöiden summa on hypotenuusan neliö a² + b² = c².
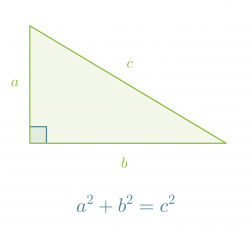
Klikkaa kuva suuremmaksi!
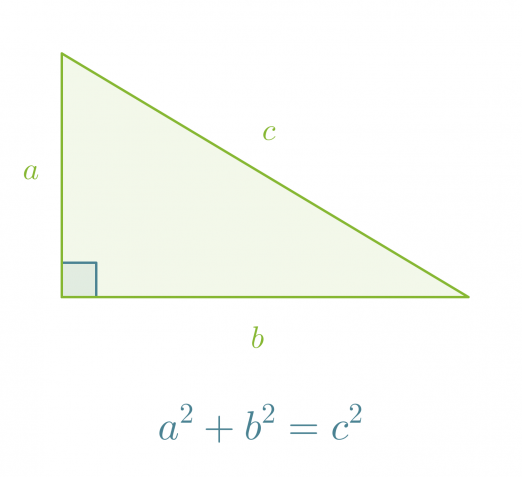
Klikkaa kuva suuremmaksi!
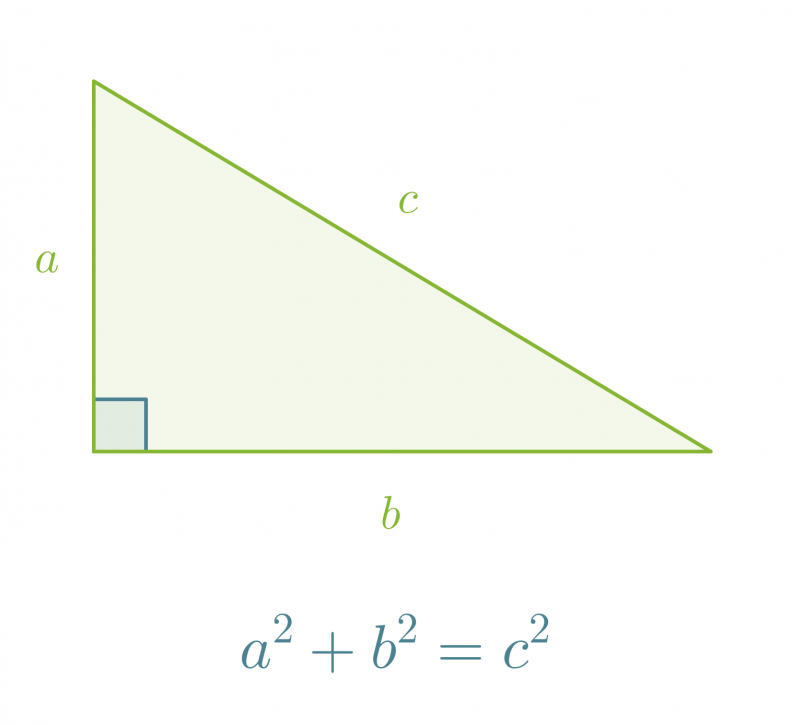
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
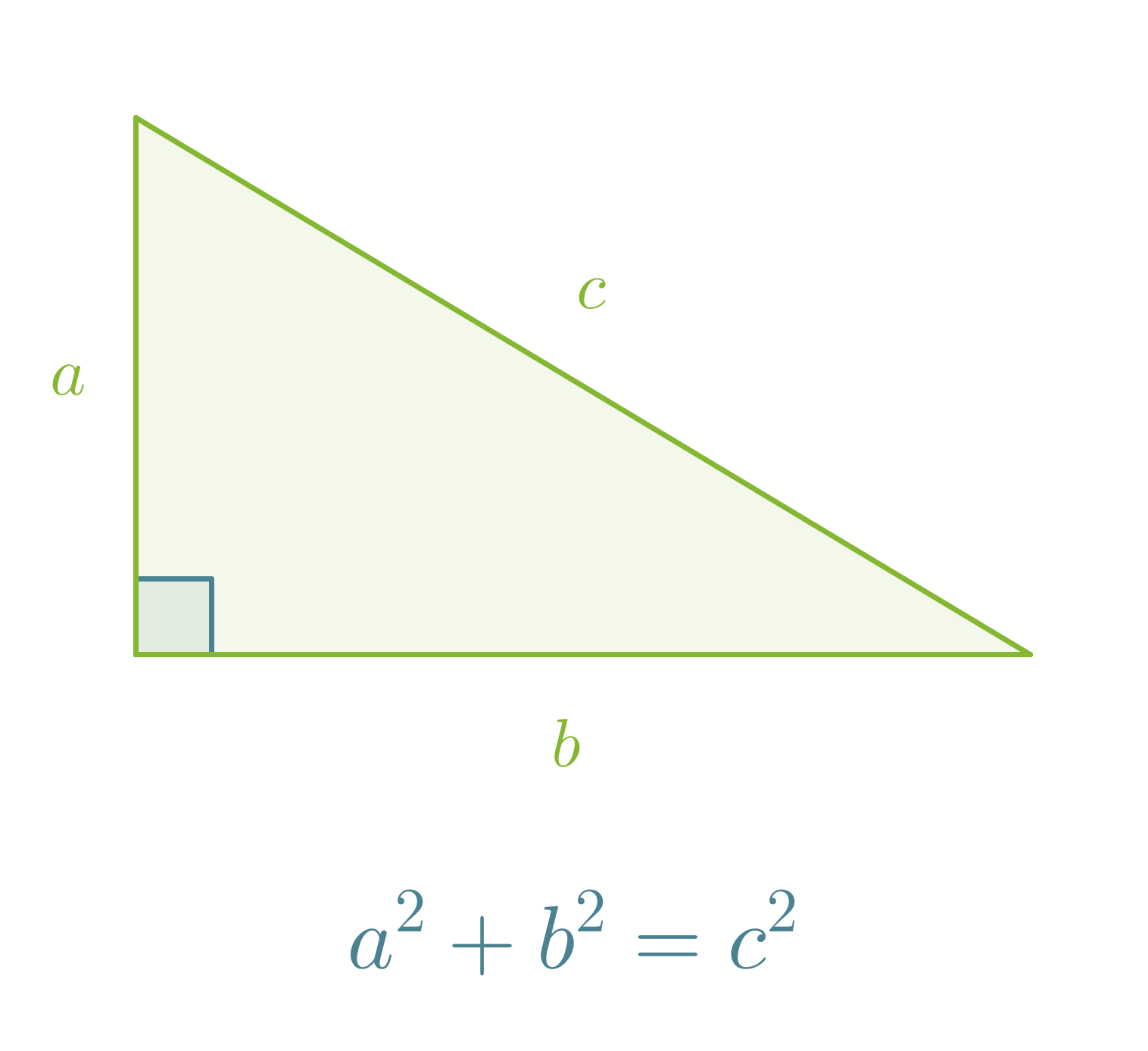
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
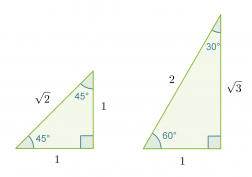
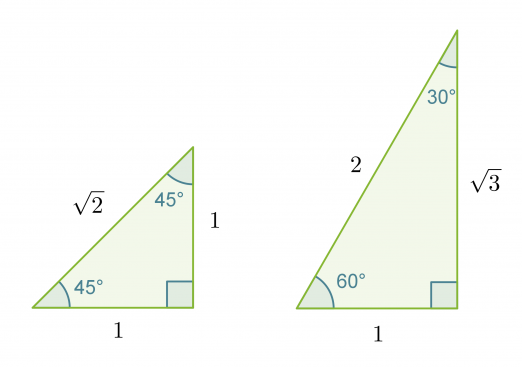
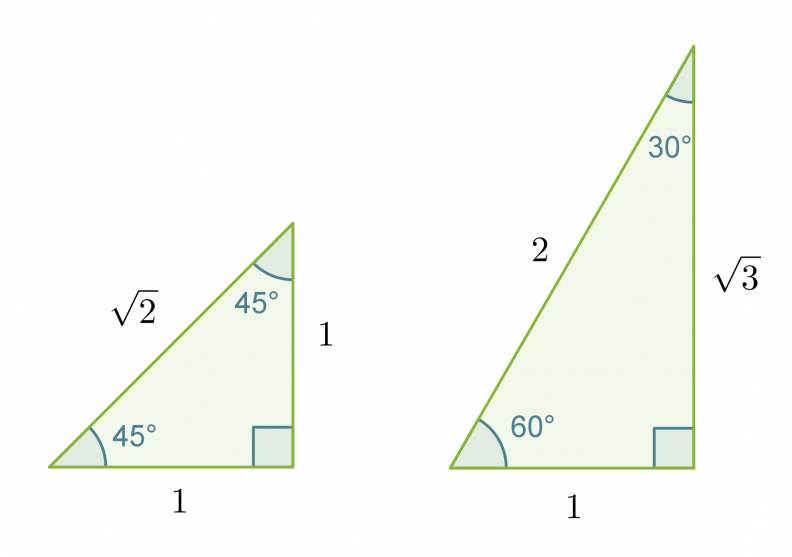
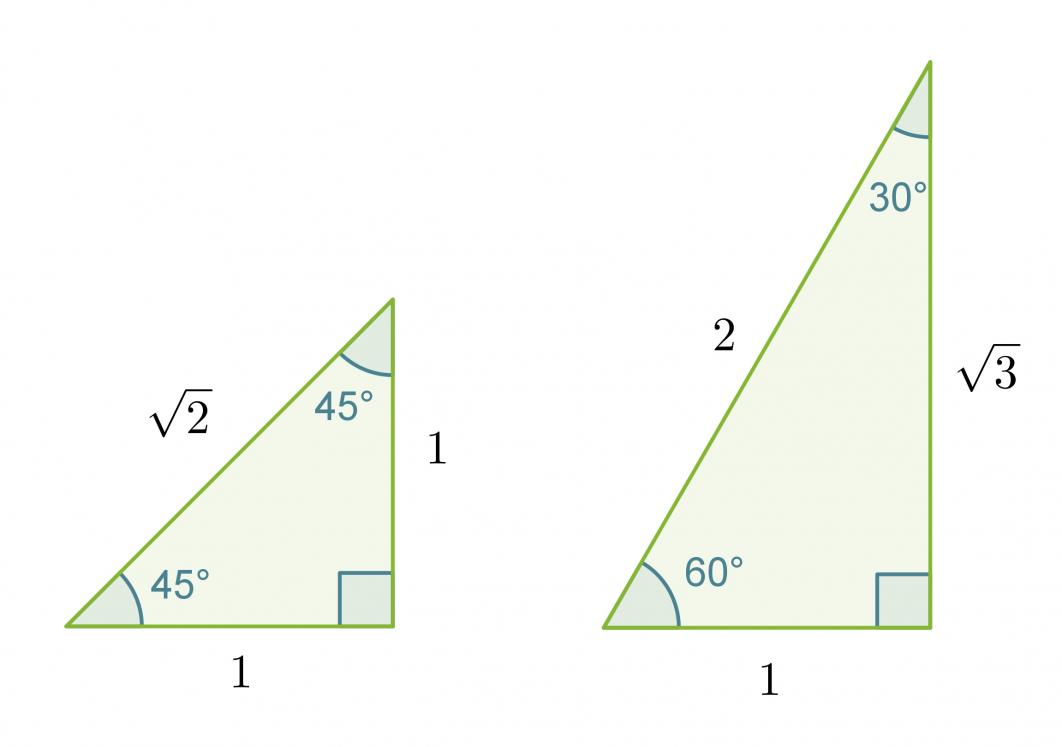
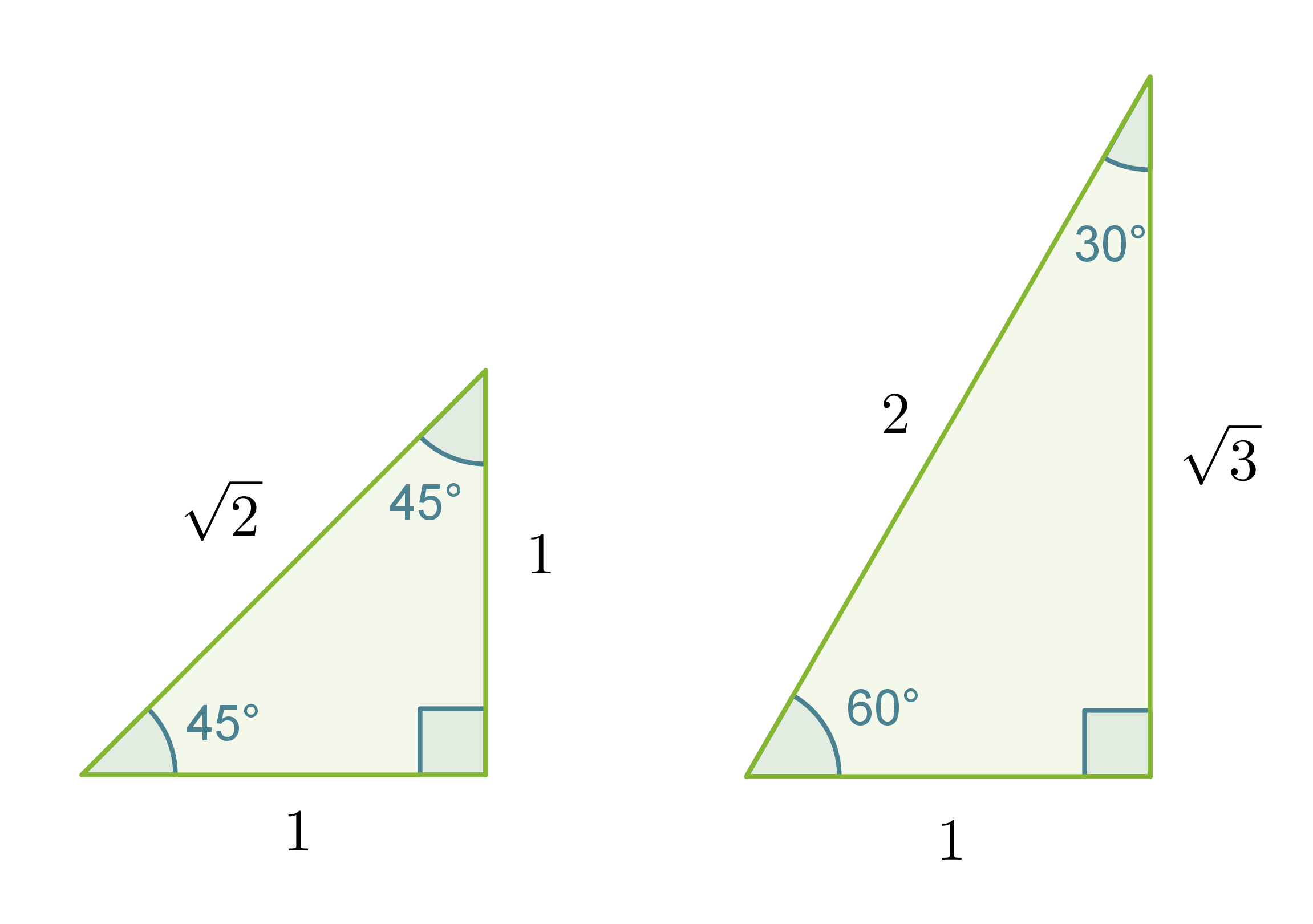
Jos pythagoraan lausetta sovelletaan neliöön ja tasasivuiseen kolmioon, muodostuu ns. muistikolmiot. Muistikolmioiden ideana on se, että niiden avulla pystytään selvittämään tarkat trigonometristen funktioiden arvot kulmille 30˚, 45˚ ja 60˚ laskinta käyttämättä.
Esimerkki 1.
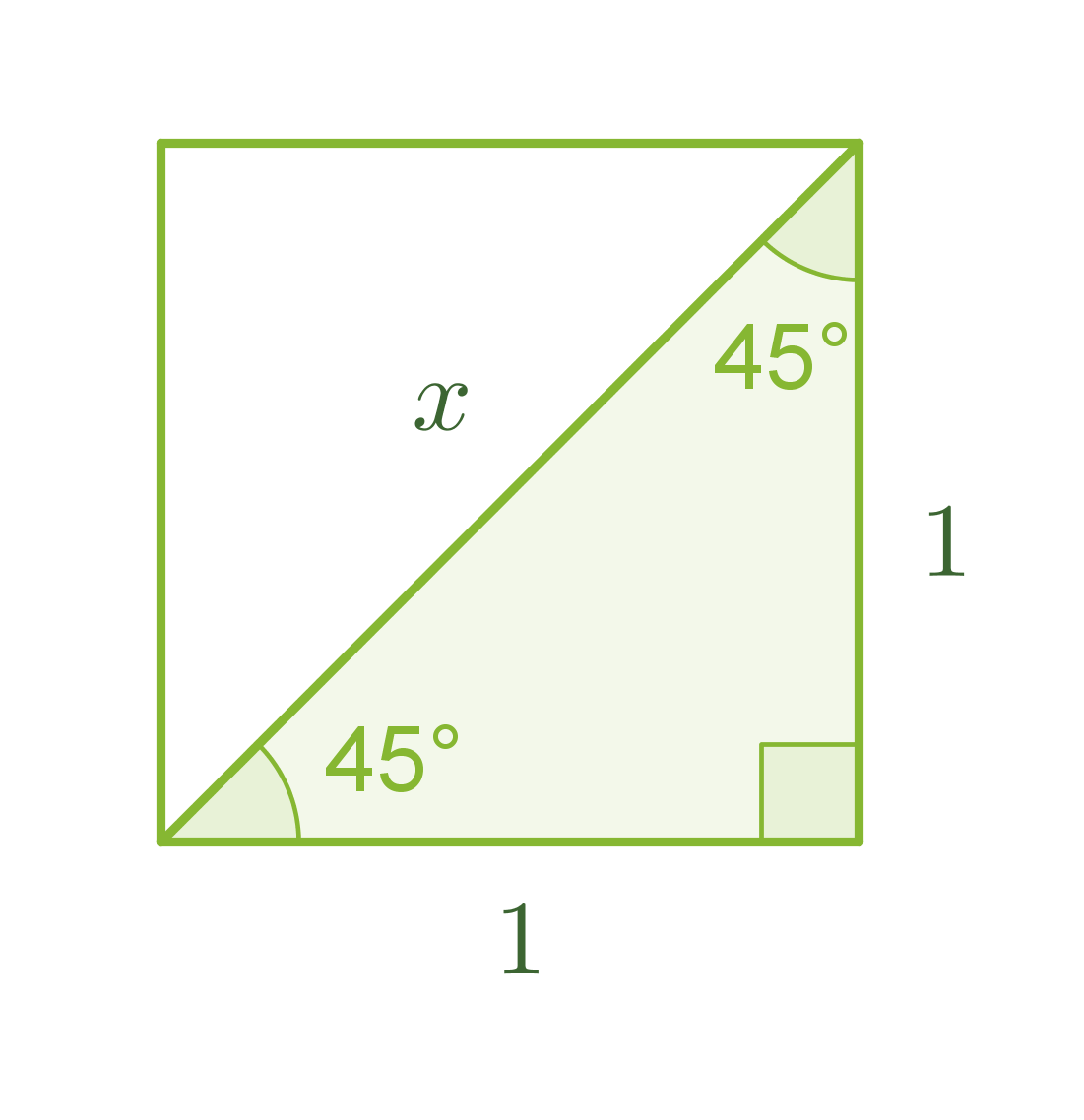
Tarkastellaan neliötä, jonka sivun pituus on 1. Lasketaan Pythagoraan lauseen avulla neliön lävistäjän pituus x.
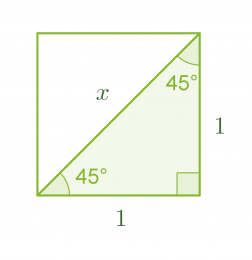
Klikkaa kuva suuremmaksi!
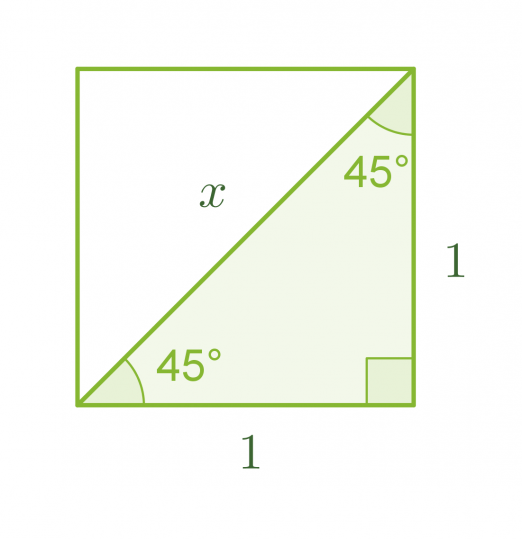
Klikkaa kuva suuremmaksi!
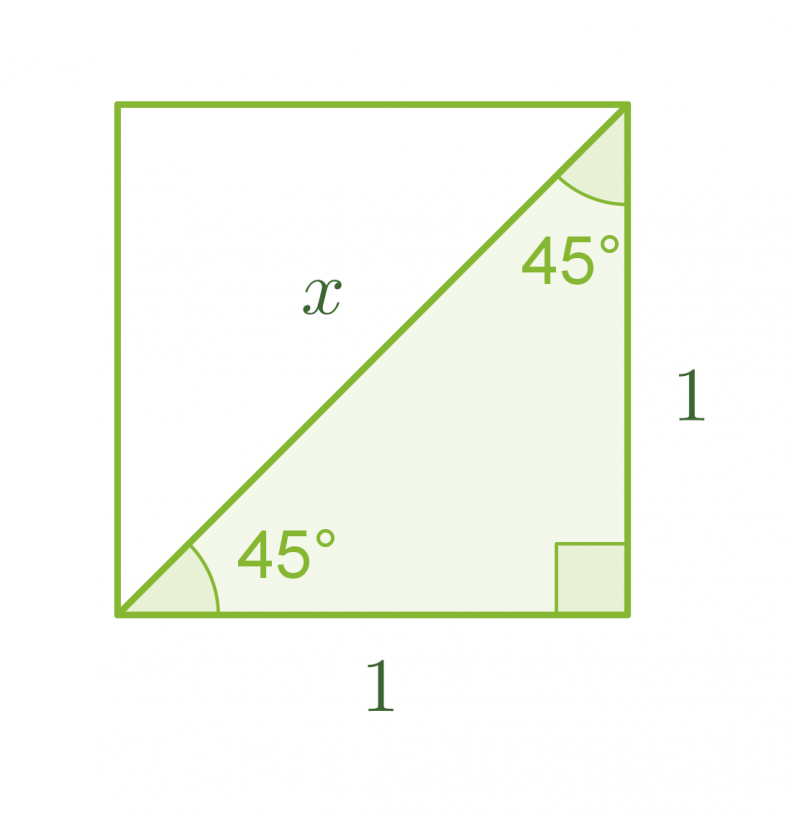
Klikkaa kuva suuremmaksi!
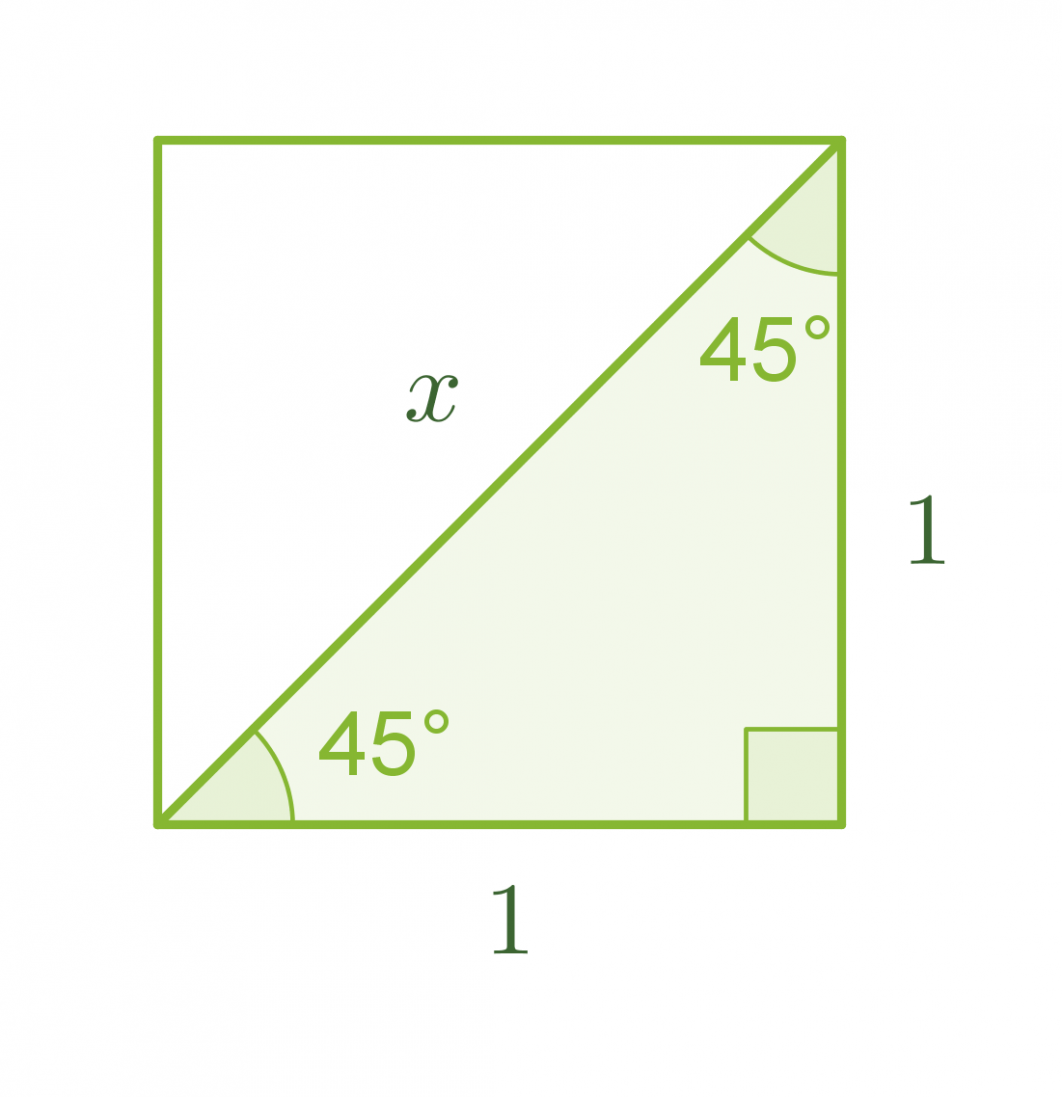
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
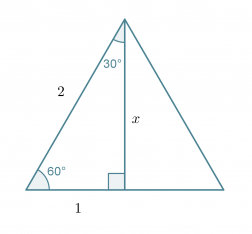
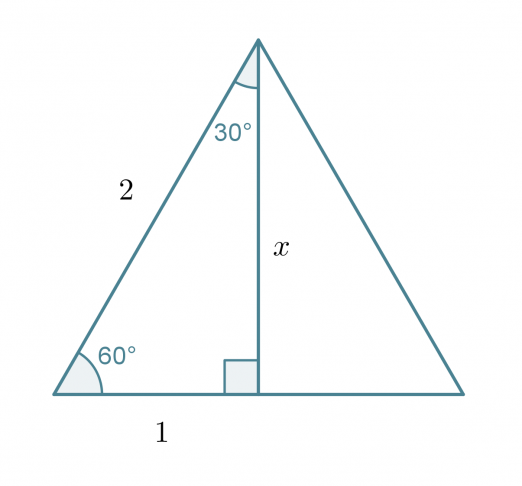
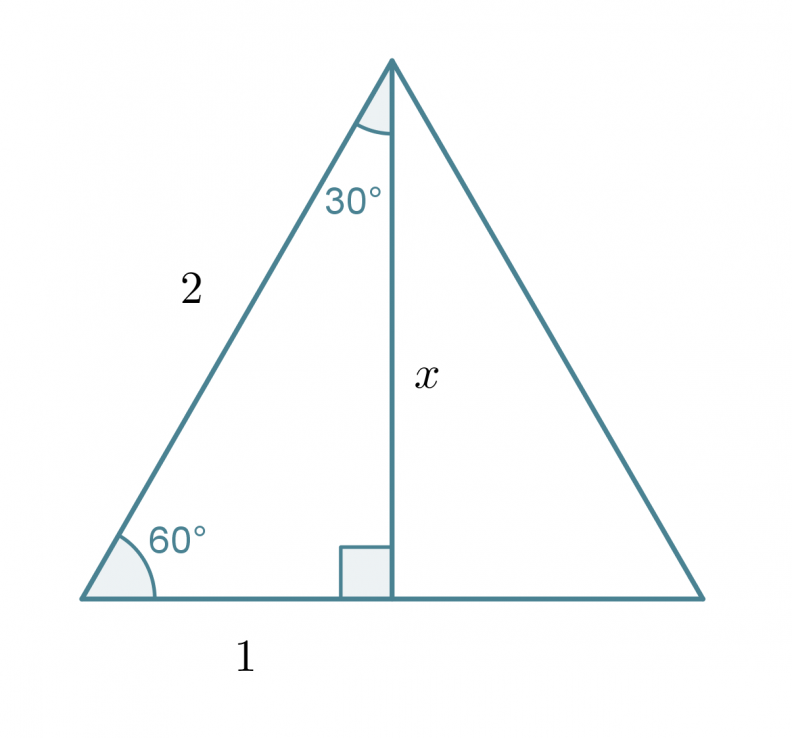
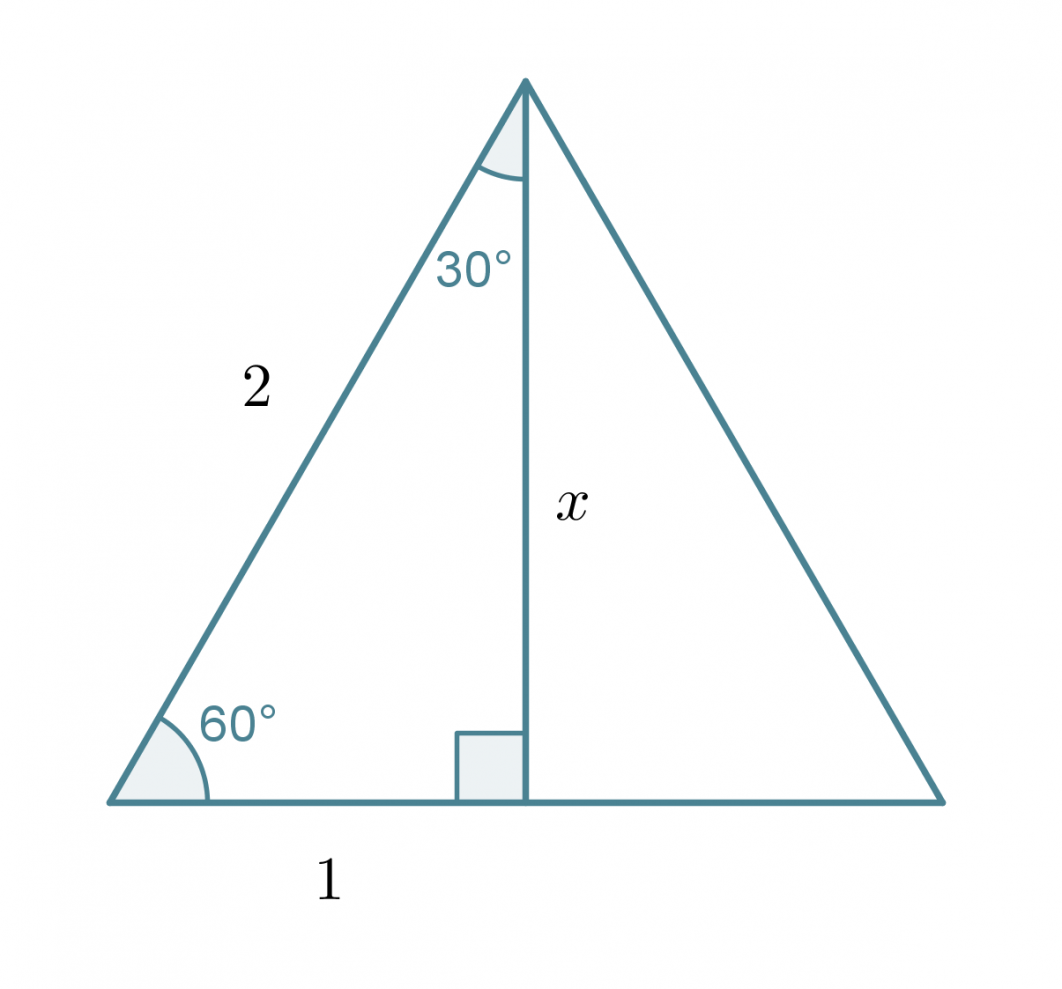
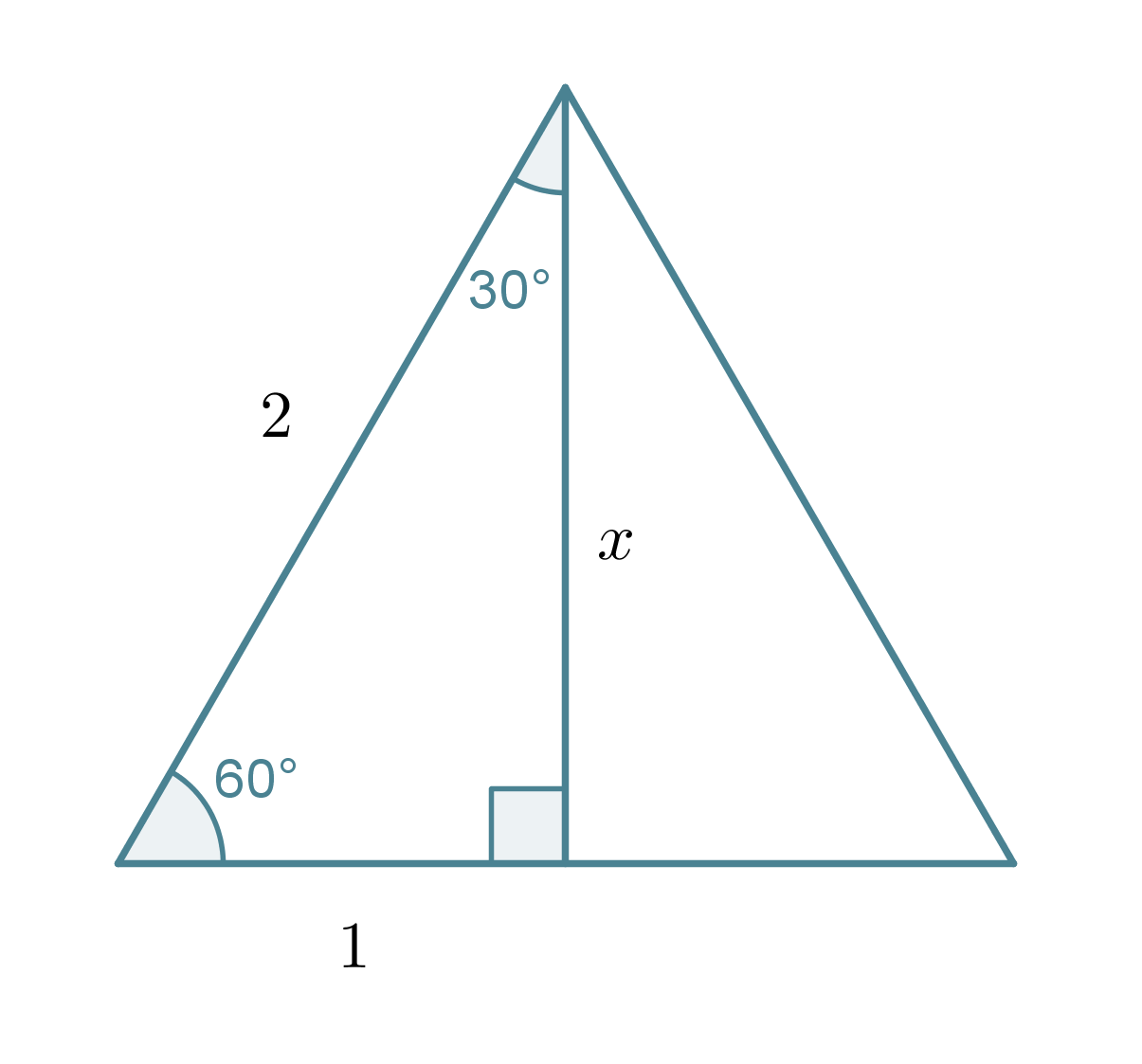
Tarkastellaan tasasivuista kolmiota, jonka sivun pituus on 2. Lasketaan Pythagoraan lausetta käyttäen kolmion korkeus x.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
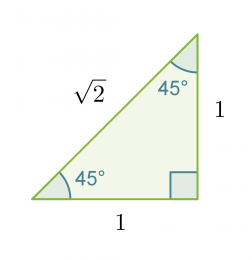
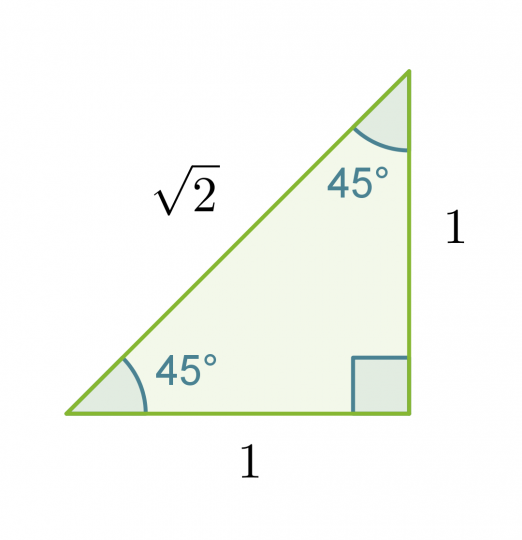
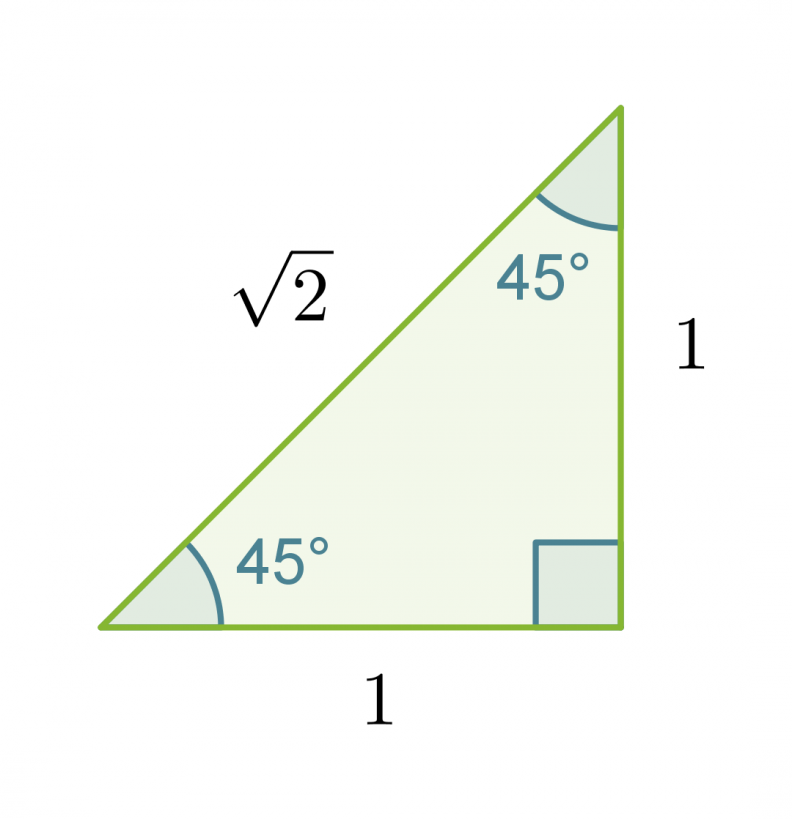
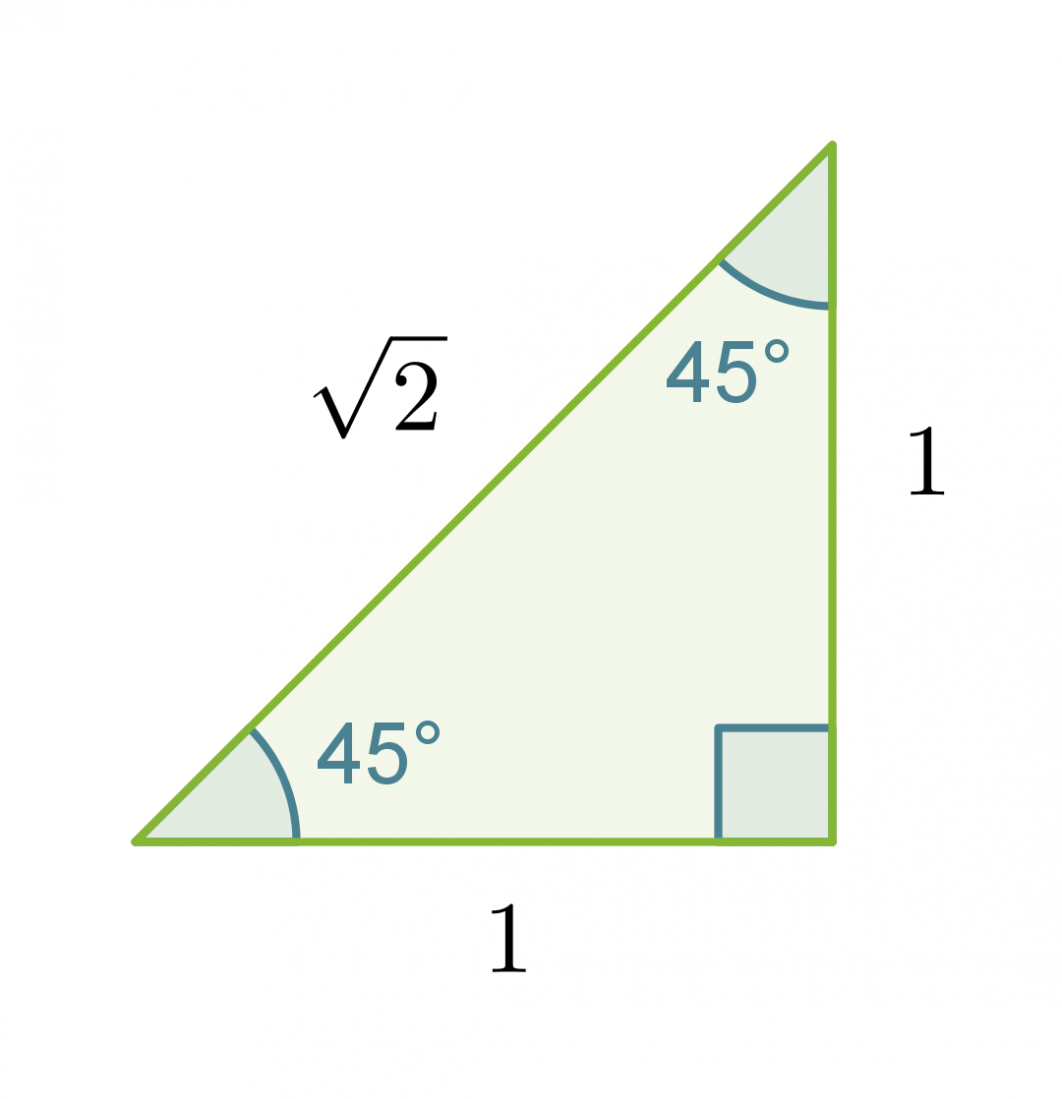
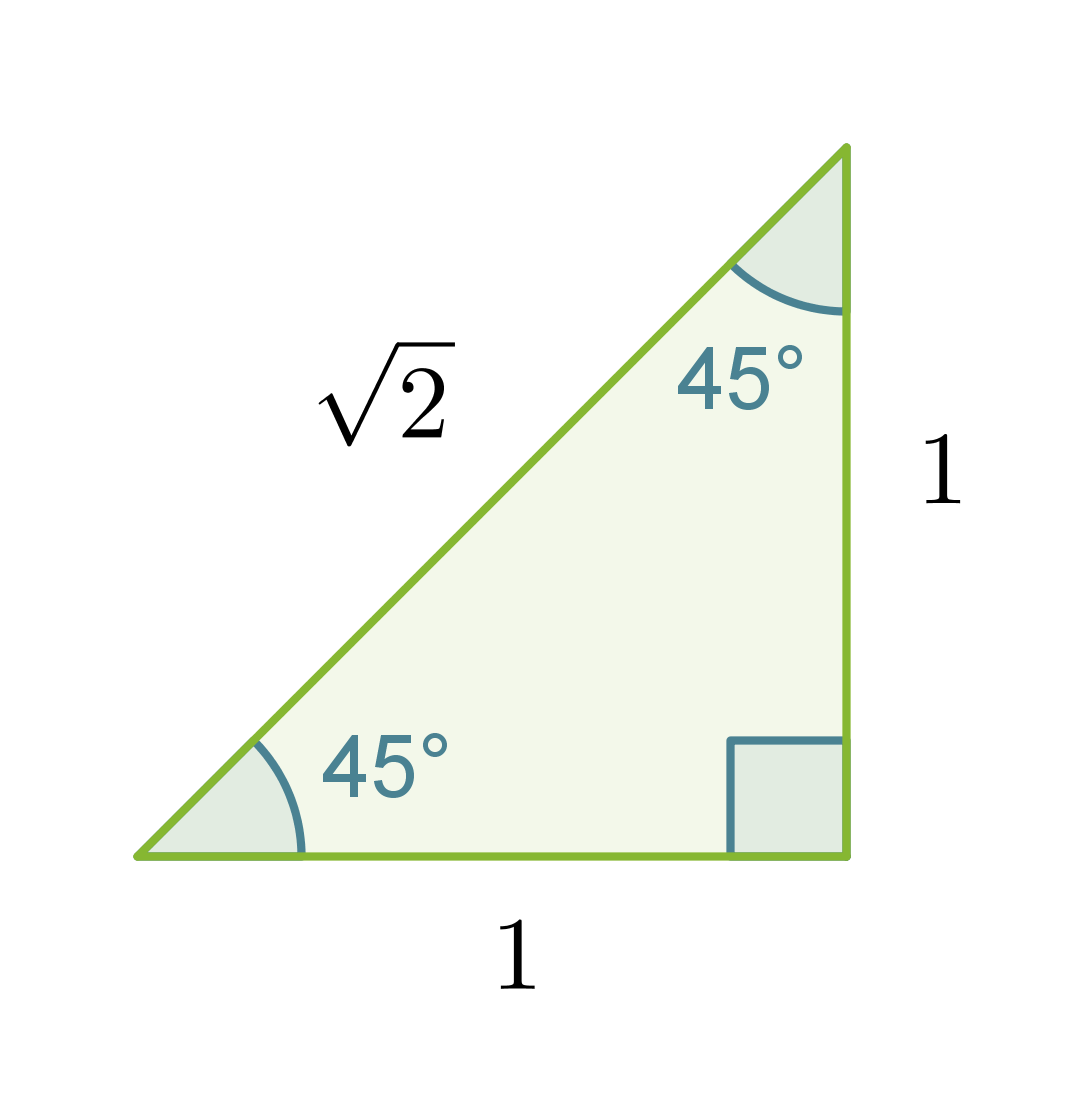
Määritetään tarkat trigonometristen funktioiden arvot kulmalle 45˚ muistikolmion avulla.
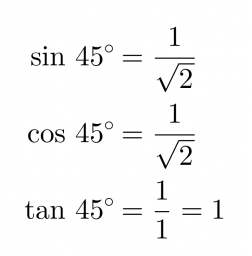
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
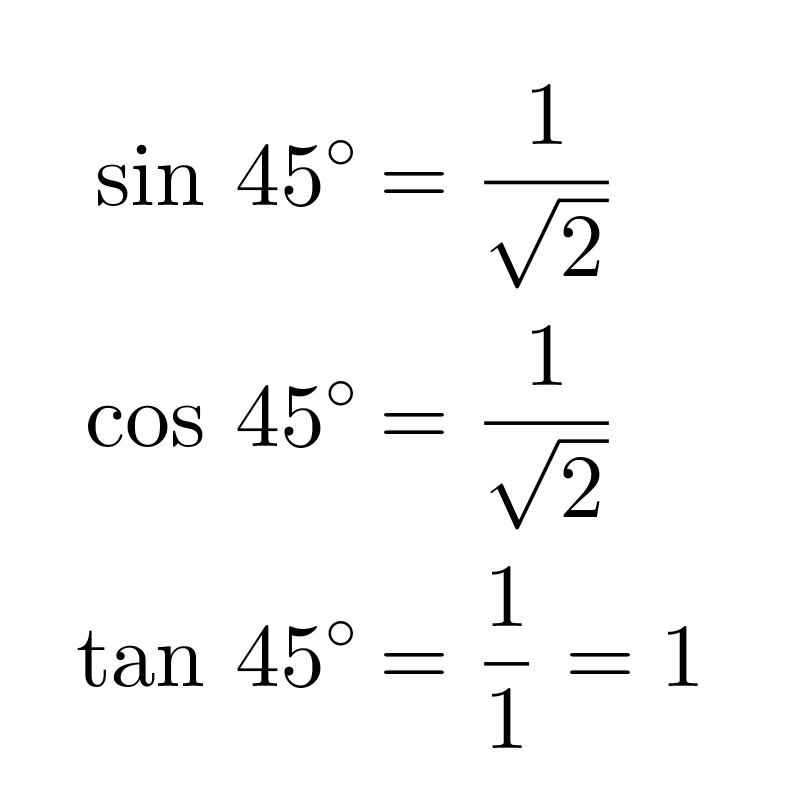
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
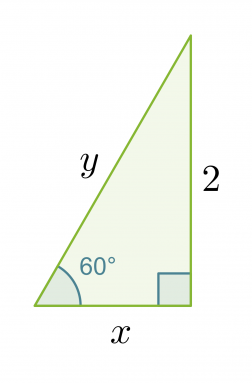
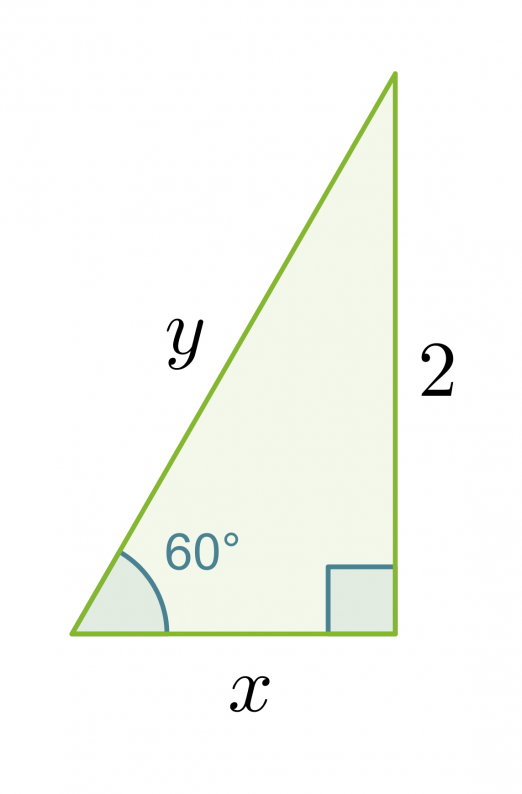
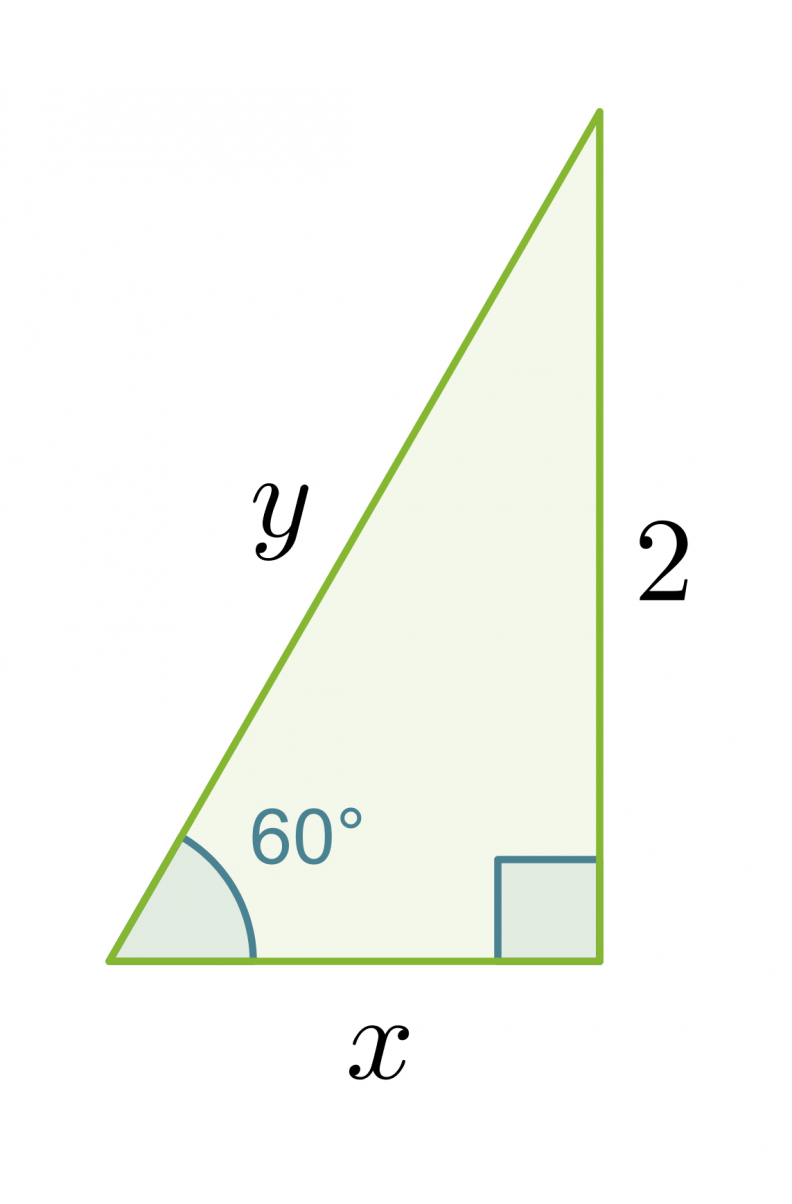
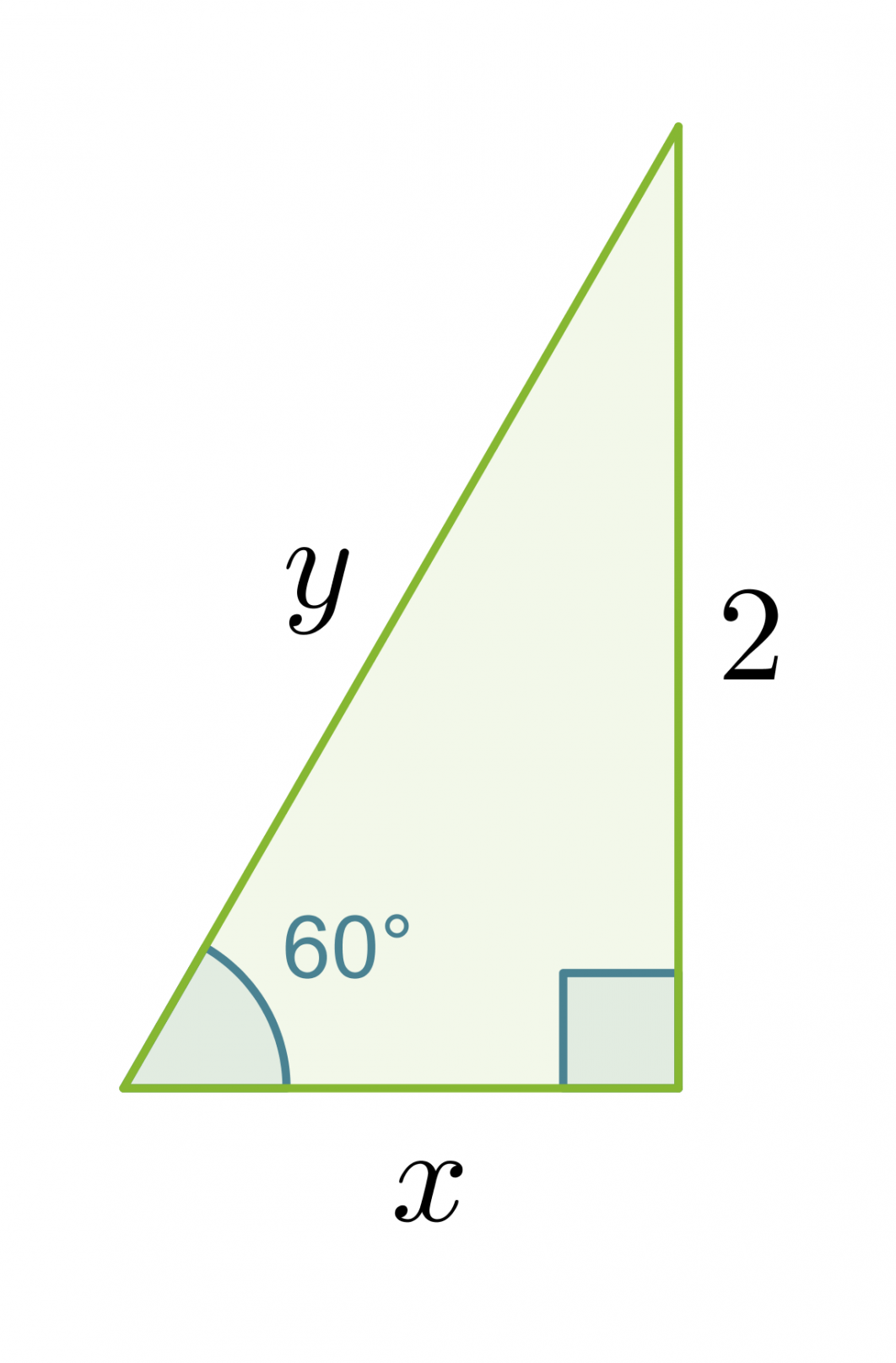
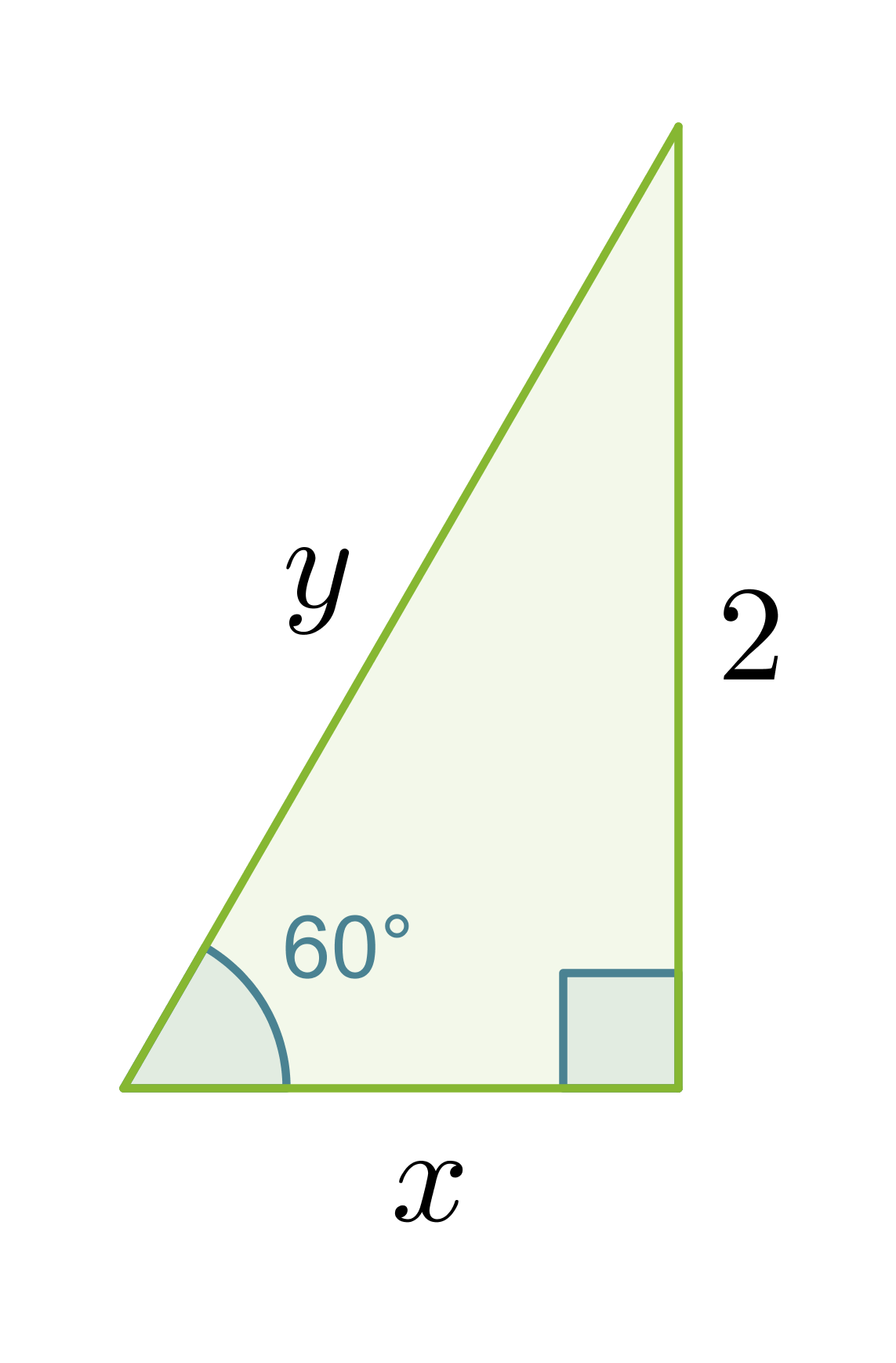
Esimerkki 4.
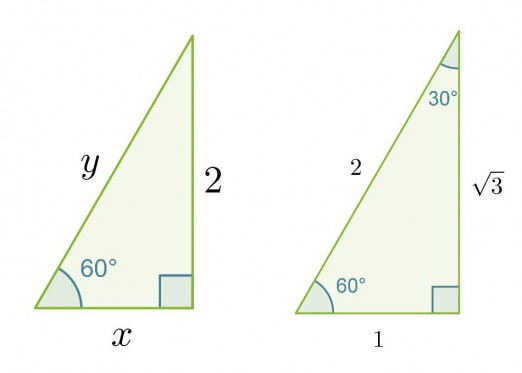
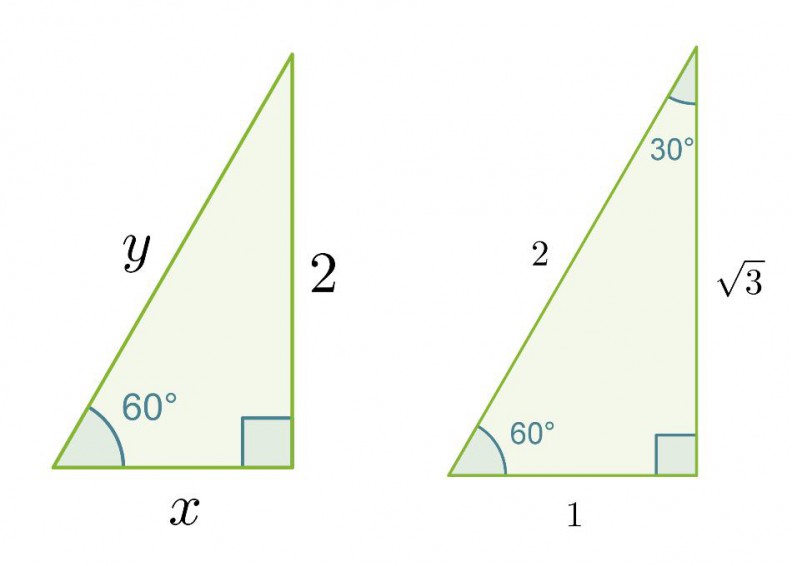
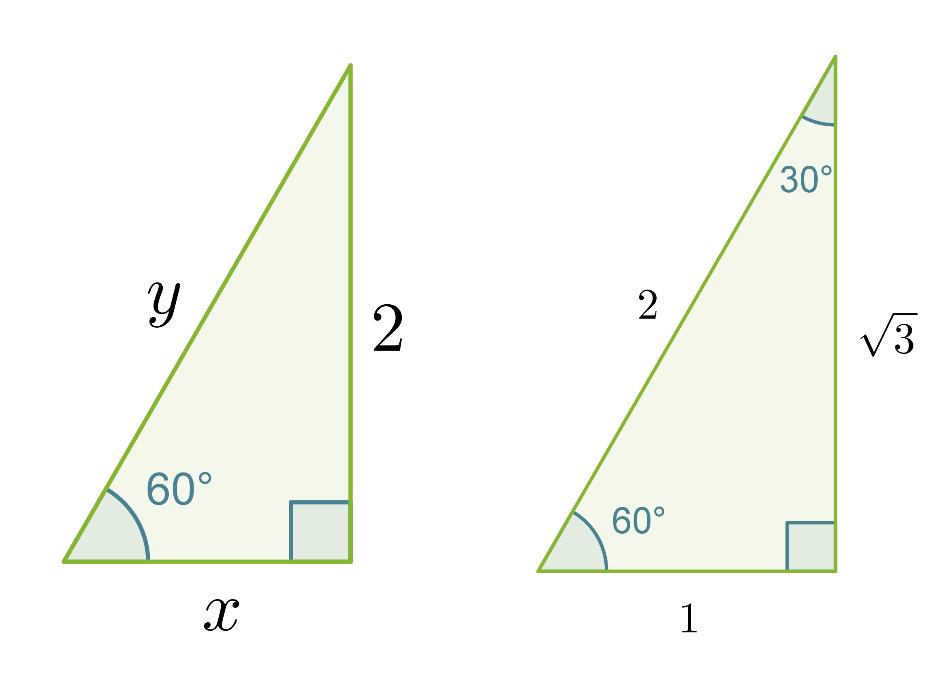
Laske muistikolmion avulla oheisen kolmion
a) kateetin x pituus
b) hypotenuusan y pituus.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
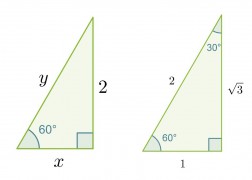
Ratkaisu:
Verrataan kolmion sivuja vastaaviin muistikolmion sivuihin ja muodostetaan verranto.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
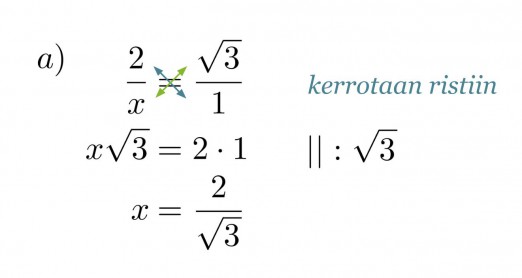
Klikkaa kuva suuremmaksi!
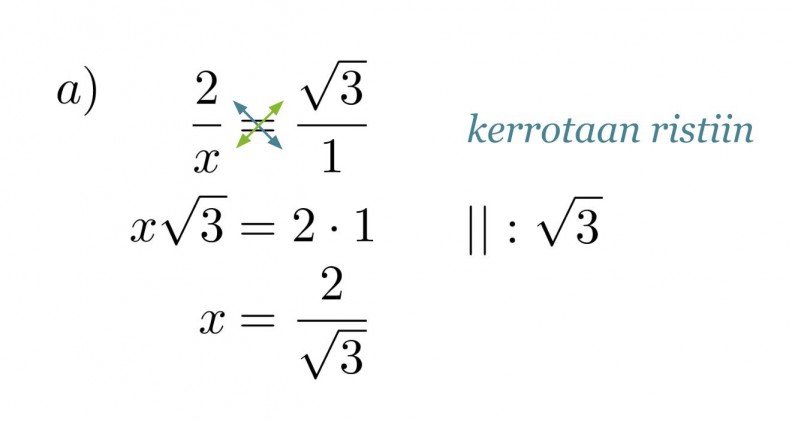
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
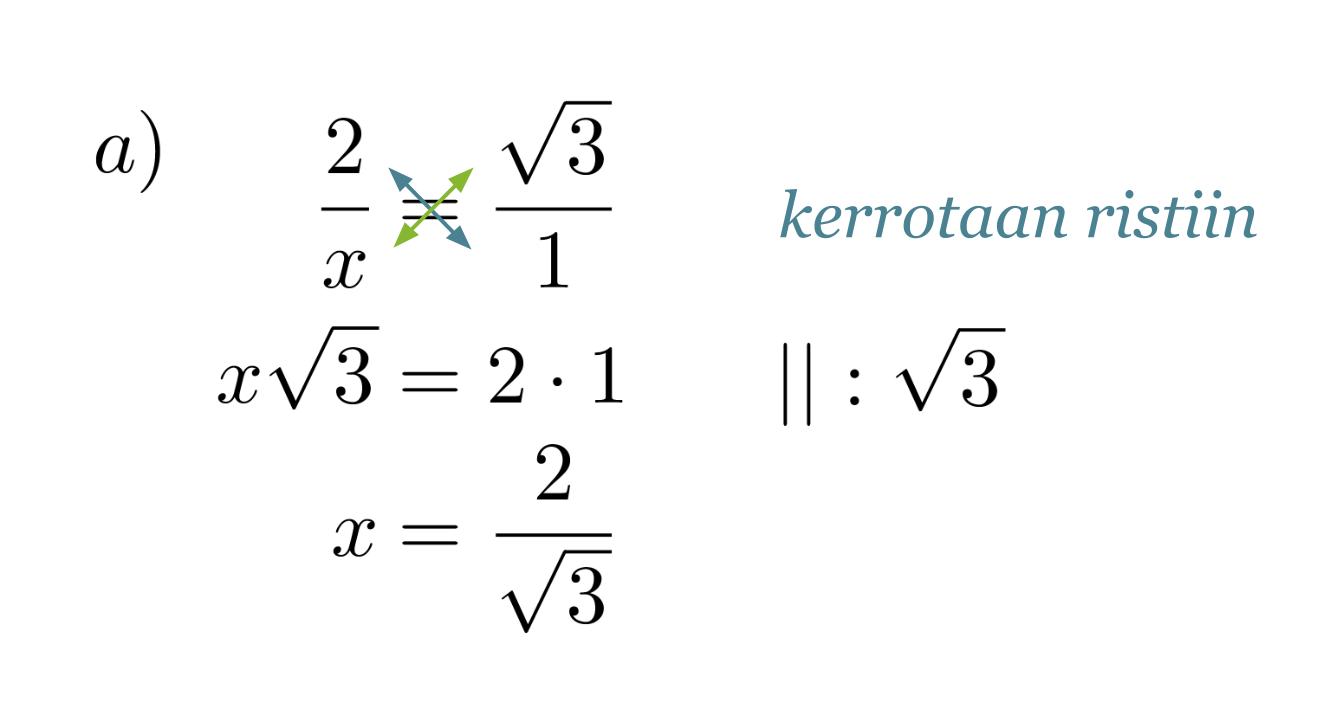
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
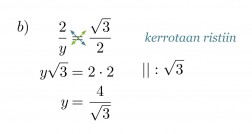
Klikkaa kuva suuremmaksi!
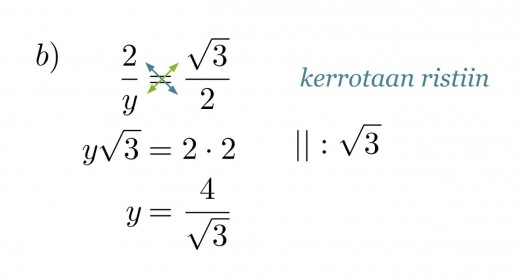
Klikkaa kuva suuremmaksi!
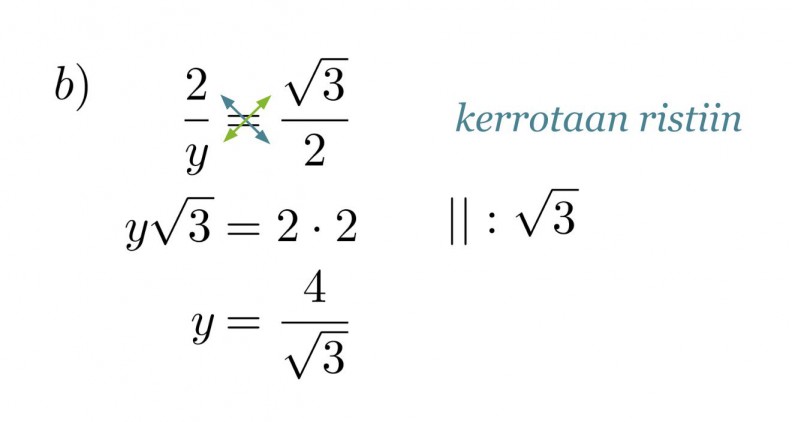
Klikkaa kuva suuremmaksi!
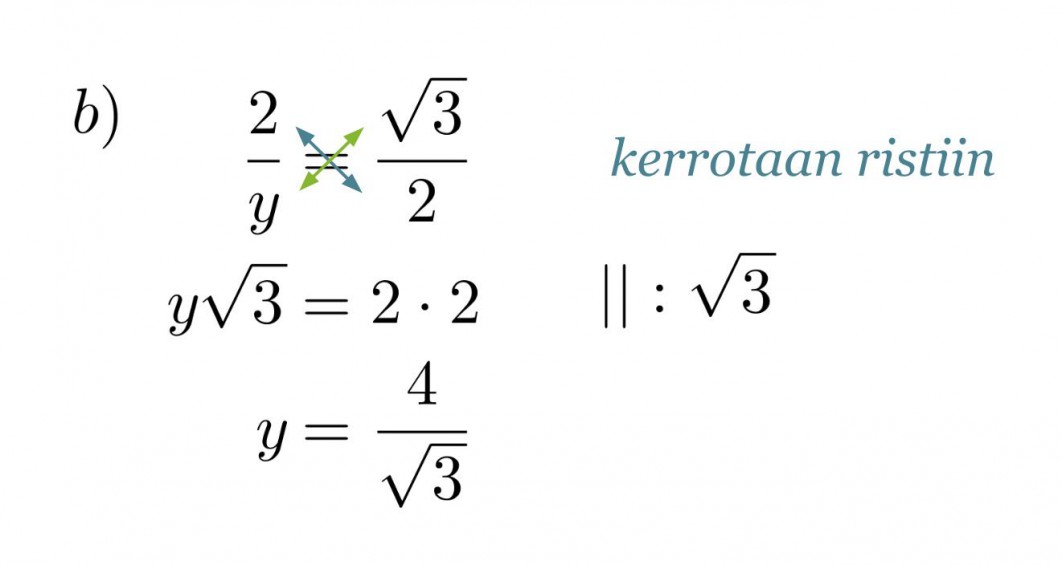
Klikkaa kuva suuremmaksi!
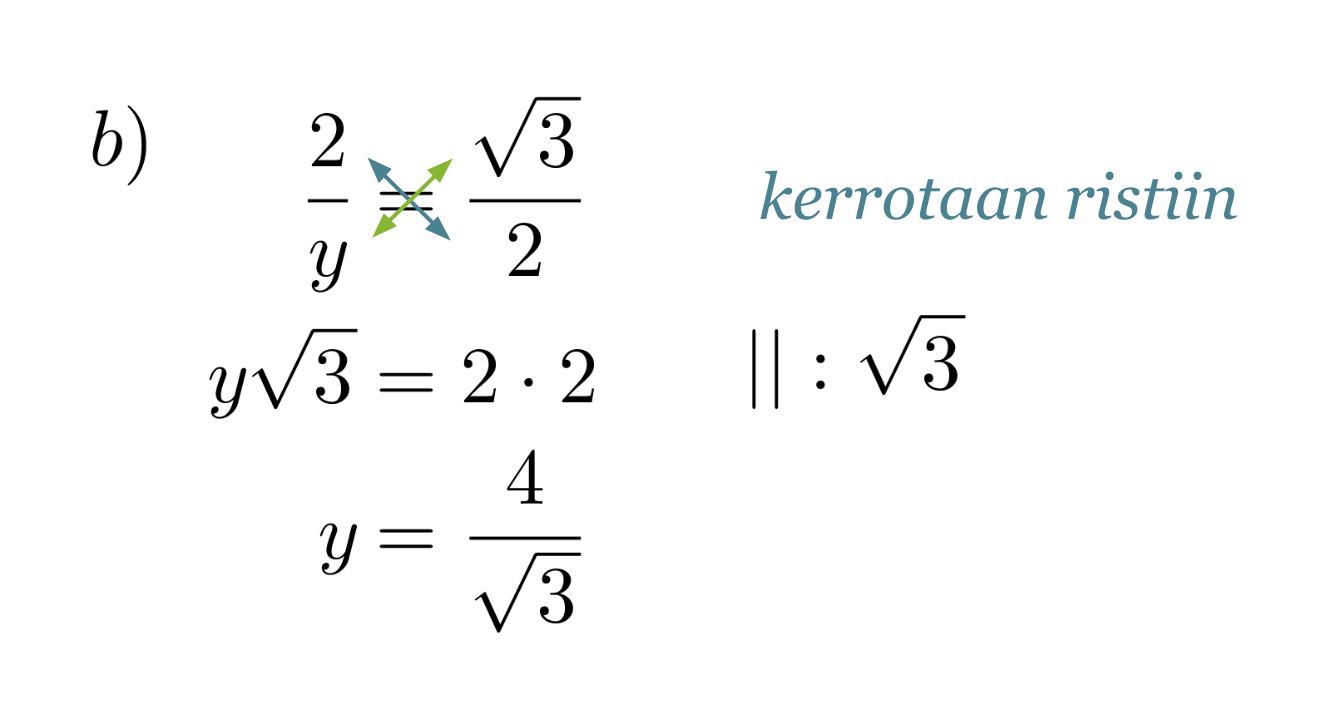
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kateetin pituus on noin 1,155 ja hypotenuusan pituus noin 2,301.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014
Muistikulmiot