6. Trigonometriset pinta-alan kaavat*
Trigonometrisiä funktioita voidaan hyödyntää myös tasokuvioiden pinta-aloja laskettaessa, jos kuviot voidaan jakaa suorakulmaisista kolmioista muodostuviin osiin.
Esimerkki 1.
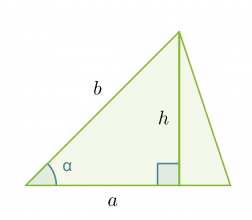
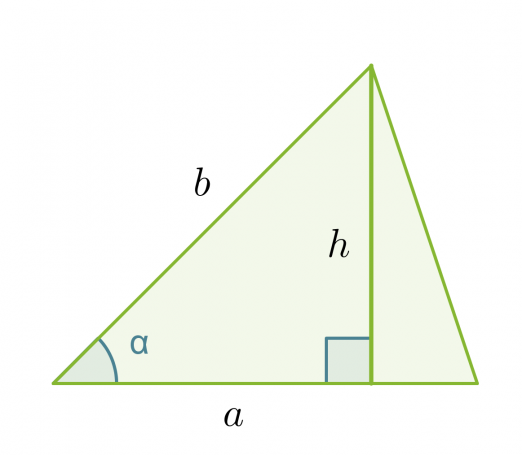
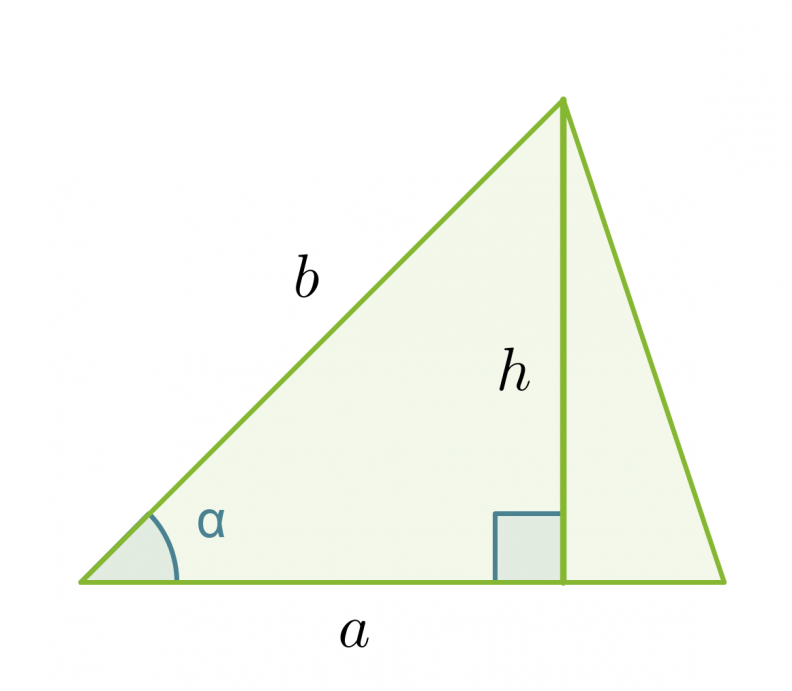
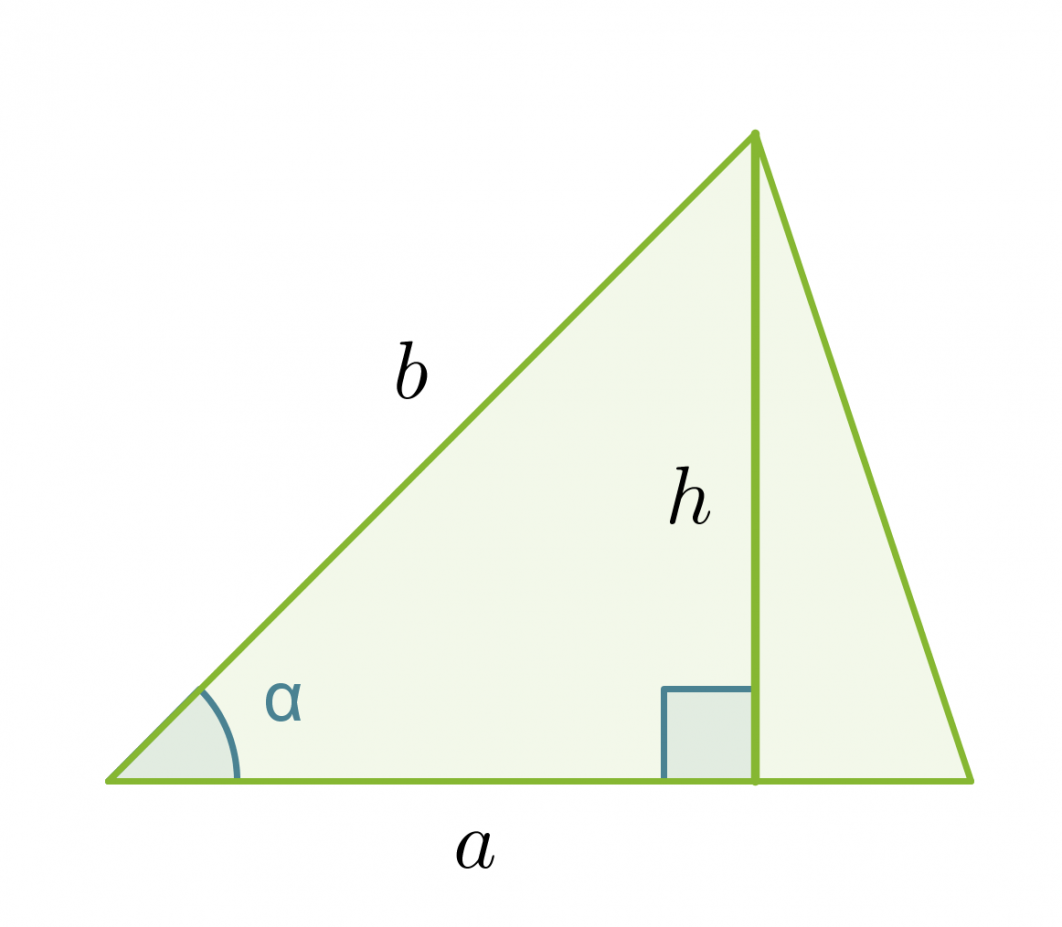
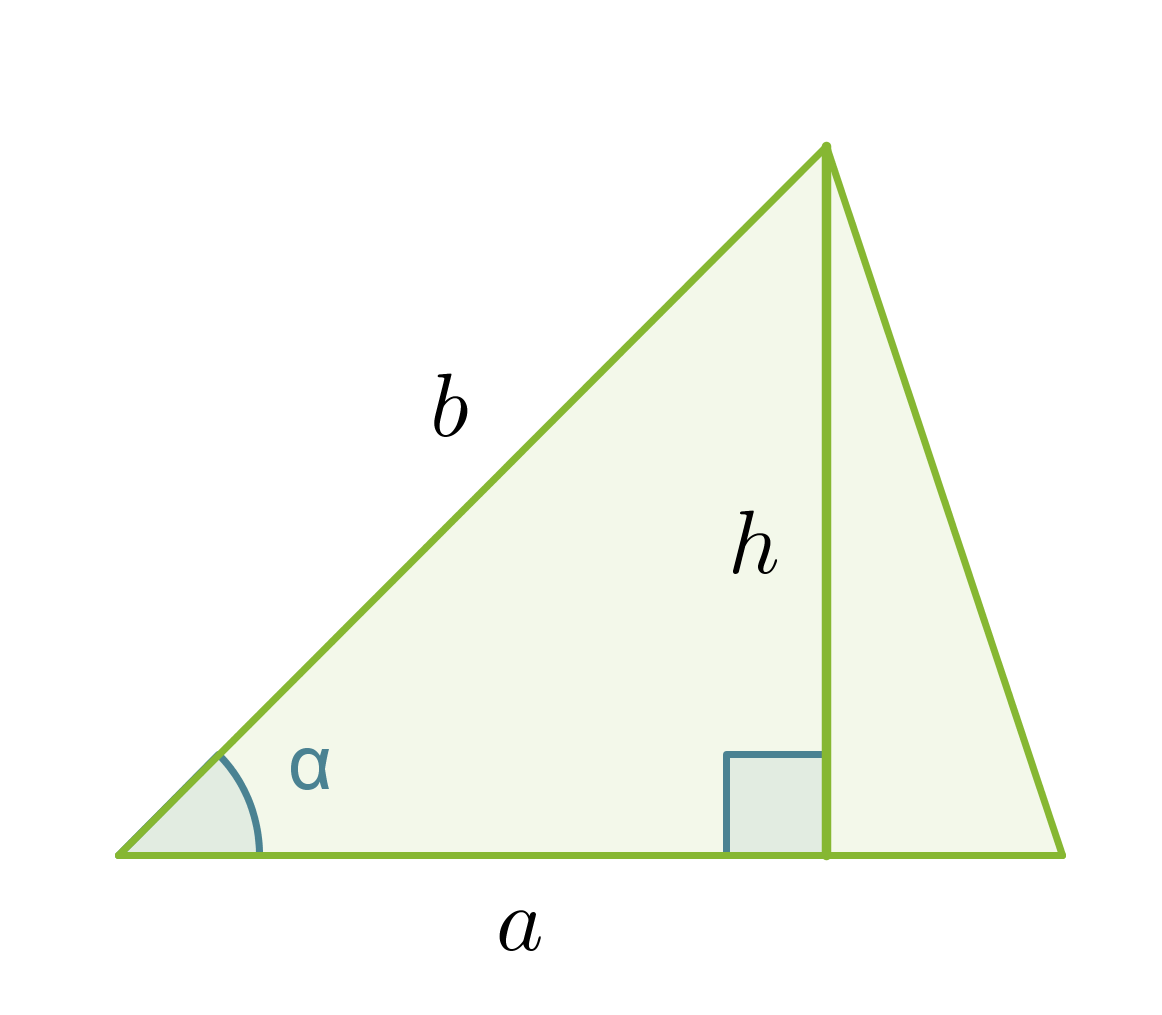
Johdetaan kaava, jolla voidaan laskea kolmion pinta-ala, kun tunnetaan kolmion kahden sivun pituus a ja b sekä näiden välisen kulman suuruus α.
Kolmion korkeus saadaan selville sinin avulla:

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kun h sijoitetaan normaaliin kolmion pinta-alan yhtälöön, muodostuu pinta-alan yhtälö, jossa korkeutta ei tarvitse erikseen ratkaista.
Kolmien pinta-ala on
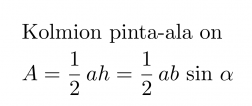
Klikkaa kuva suuremmaksi!
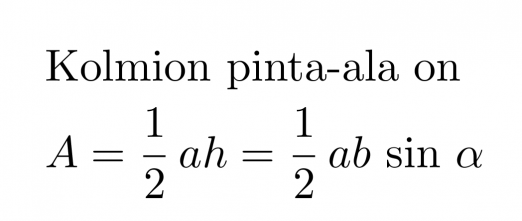
Klikkaa kuva suuremmaksi!
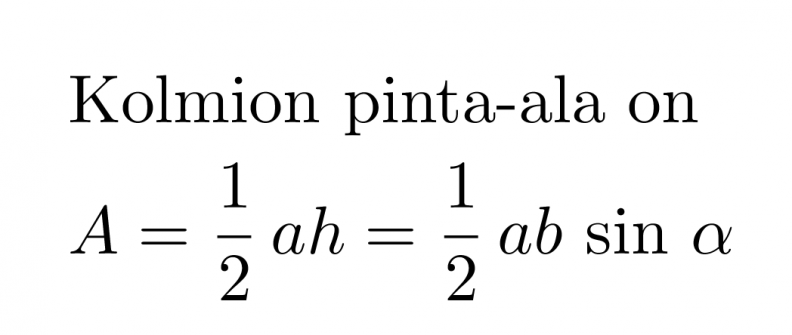
Klikkaa kuva suuremmaksi!
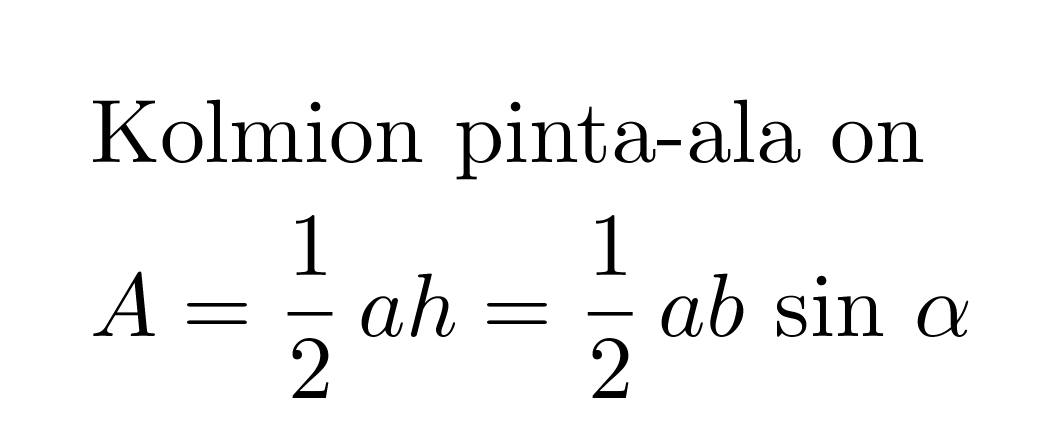
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Kaava pätee myös silloin, kun kulma α on tylppä.
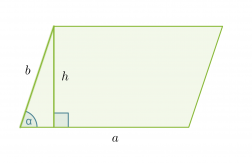
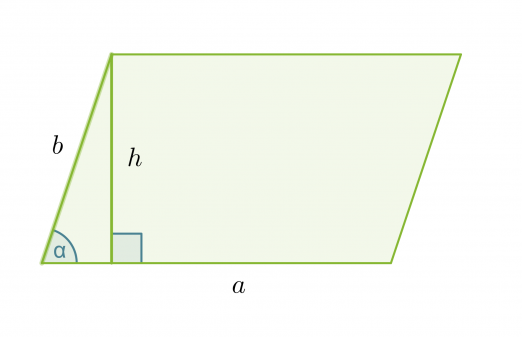
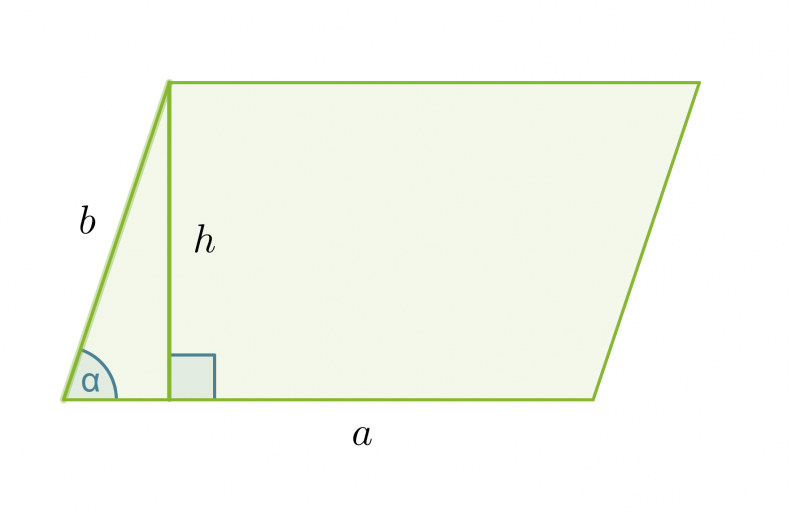
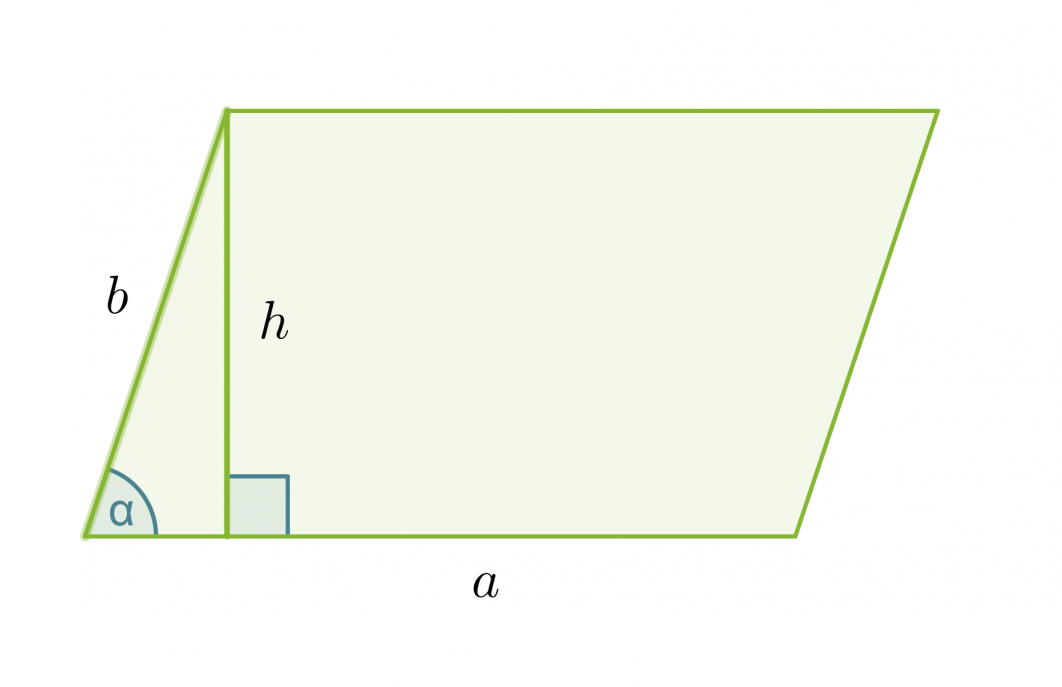
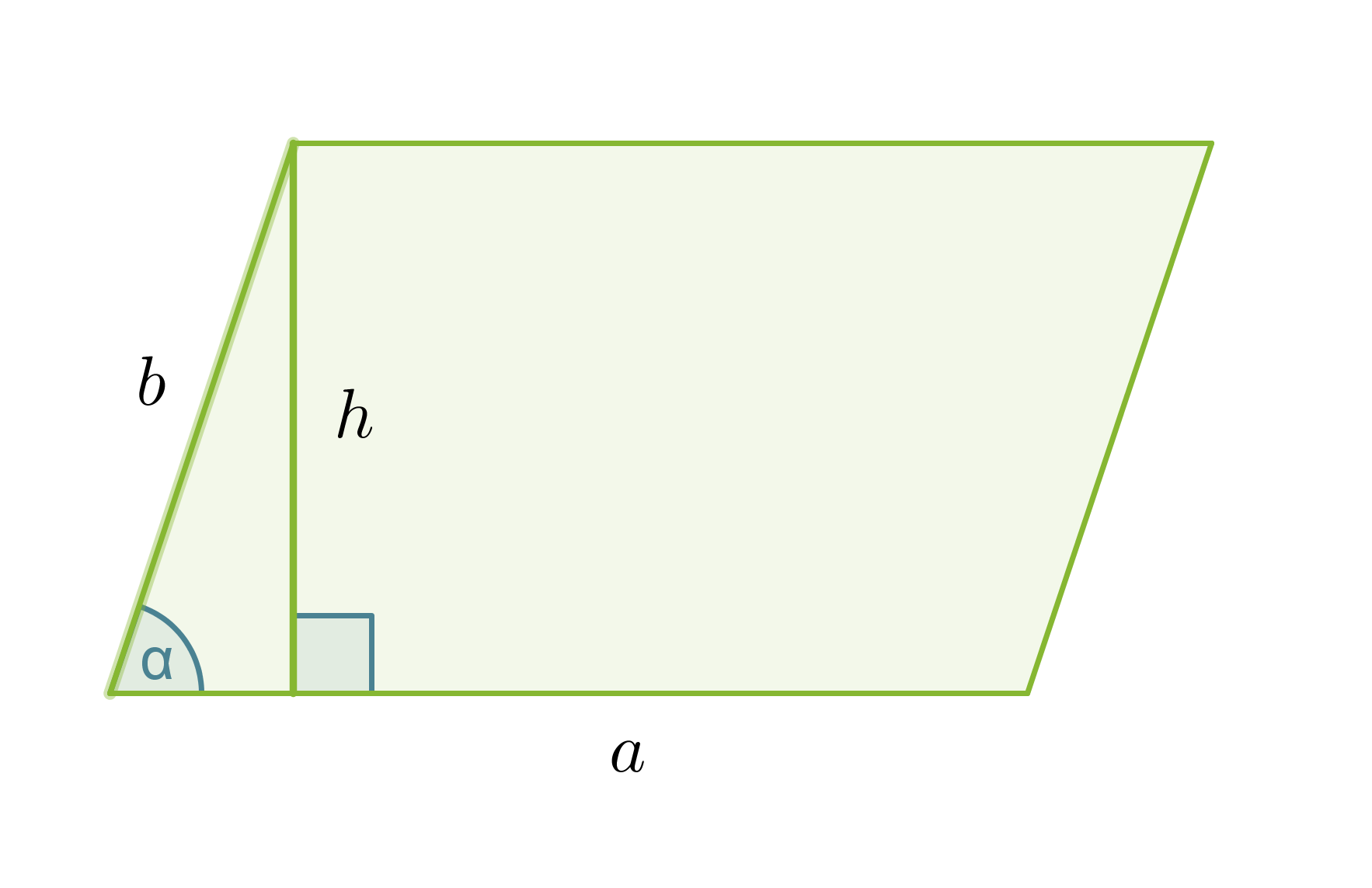
Vastaavat pinta-alan trigonometriset kaavat voidaan johtaa myös suunnikkaalle ja puolisuunnikkaalle:
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suunnikkaan pinta-ala
A = ah = ab sin α
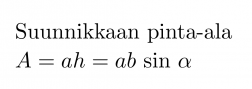
Klikkaa kuva suuremmaksi!
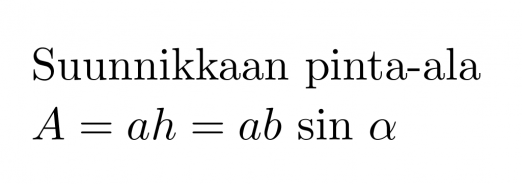
Klikkaa kuva suuremmaksi!
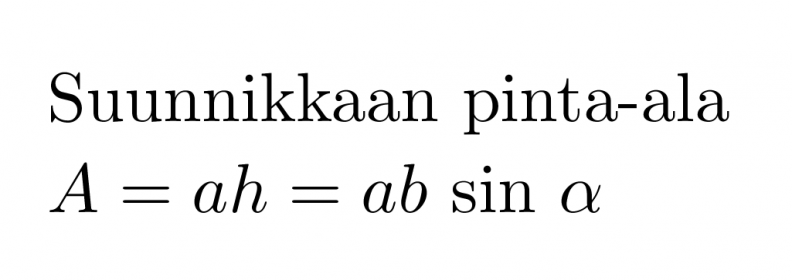
Klikkaa kuva suuremmaksi!
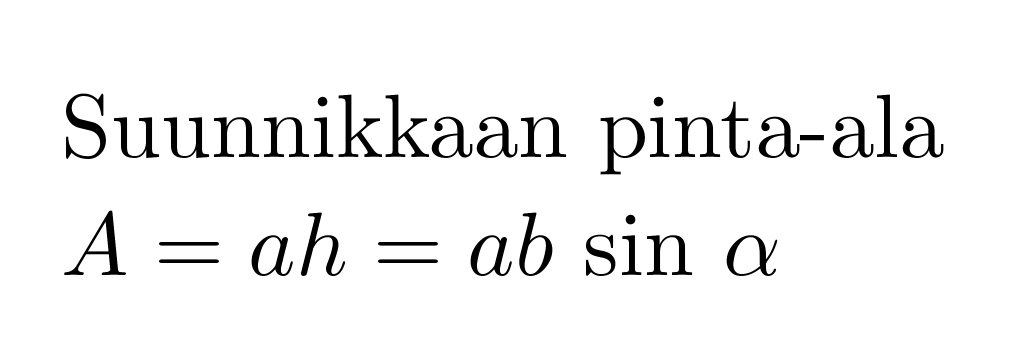
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
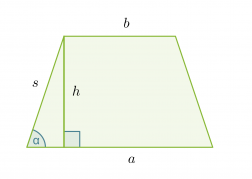
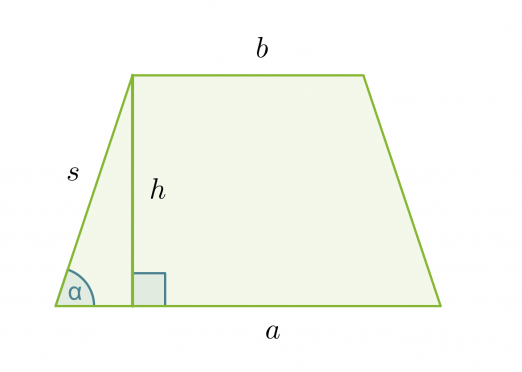
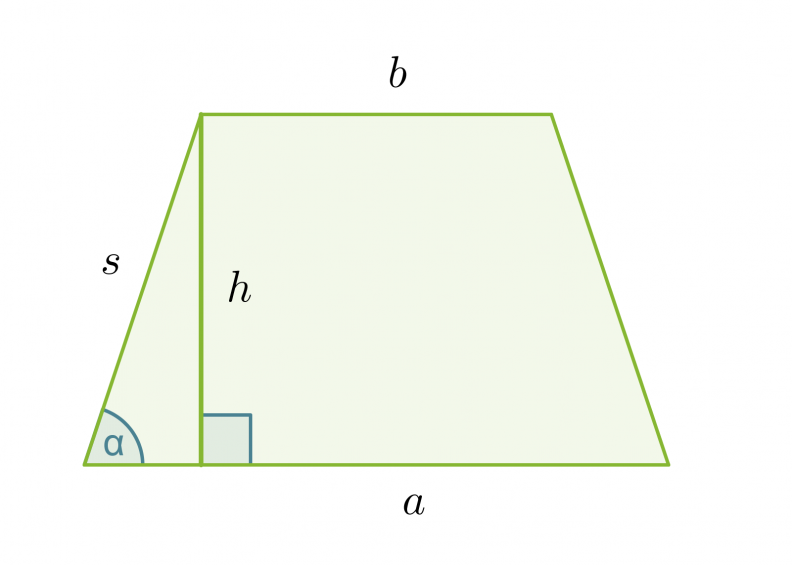
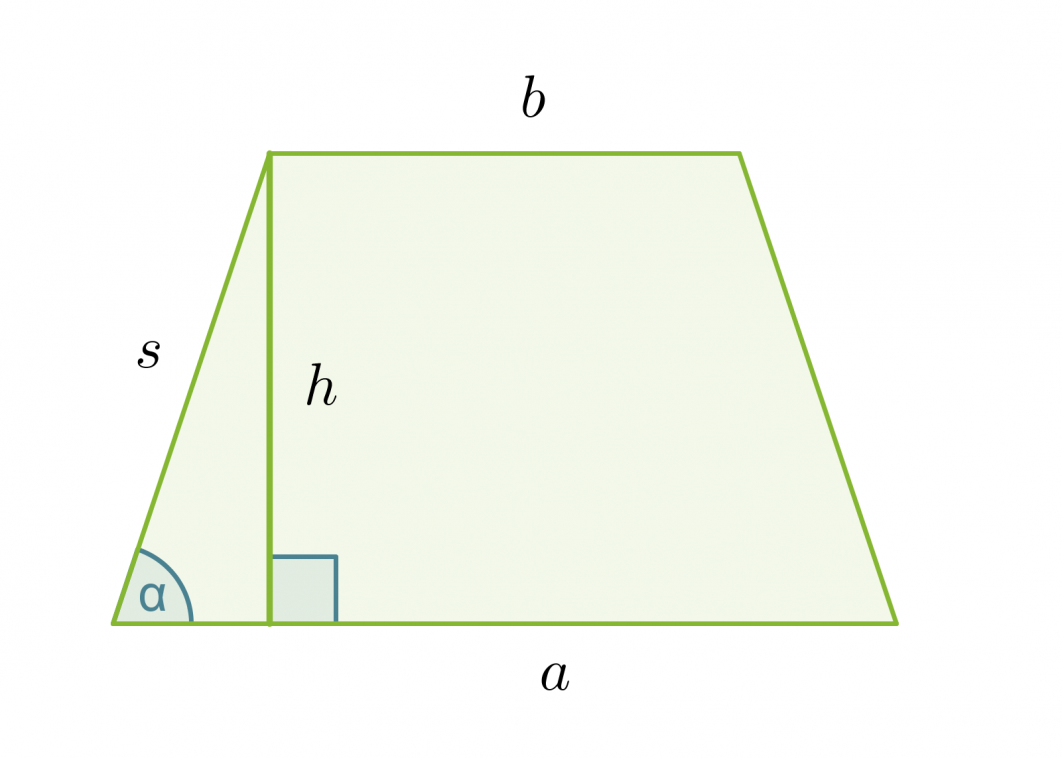
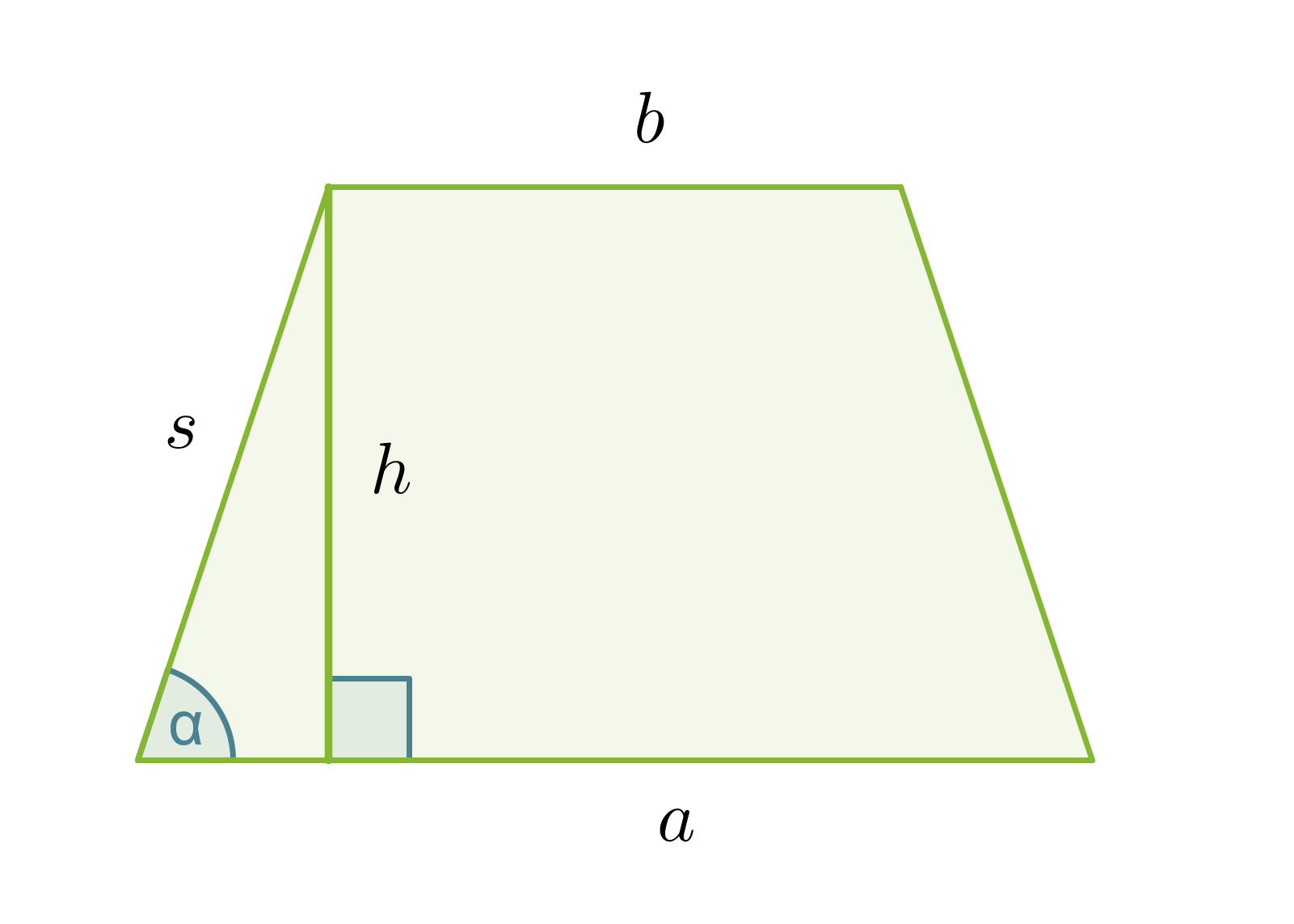
Puolisuunnikkaan pinta-ala on
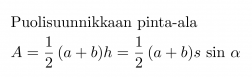
Klikkaa kuva suuremmaksi!
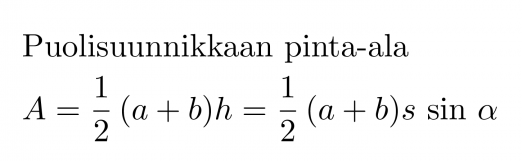
Klikkaa kuva suuremmaksi!
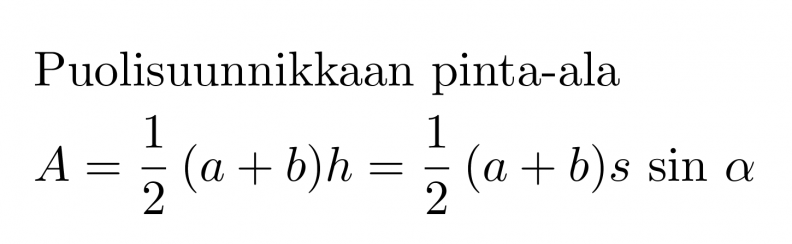
Klikkaa kuva suuremmaksi!
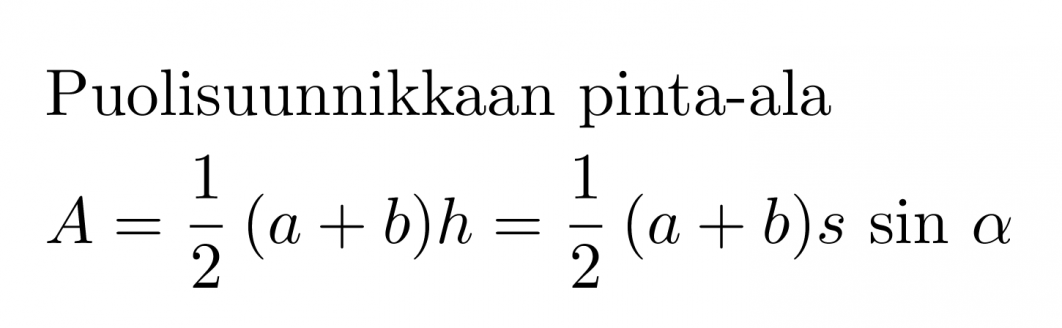
Klikkaa kuva suuremmaksi!
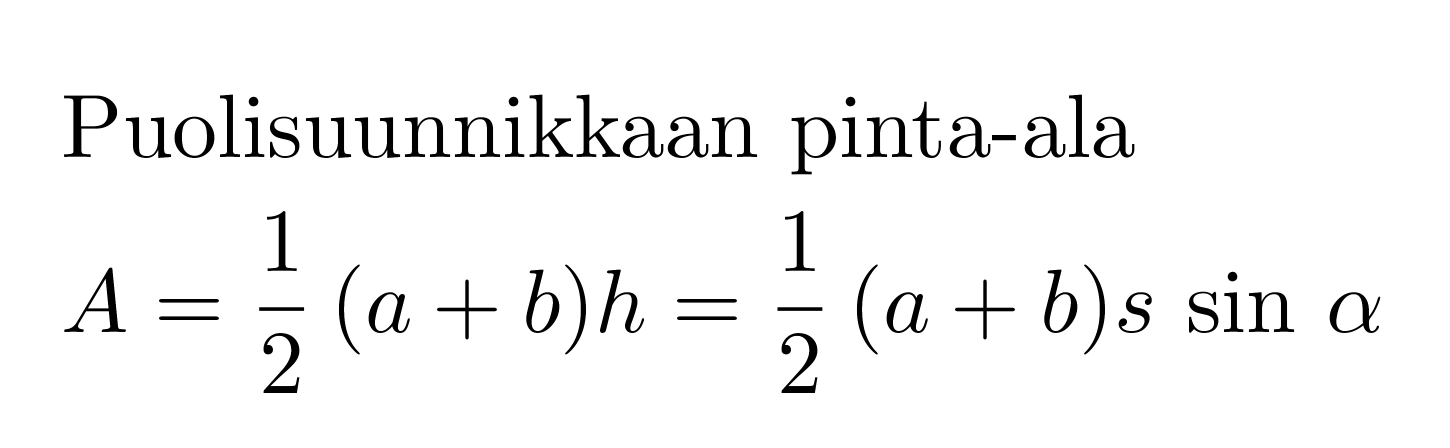
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
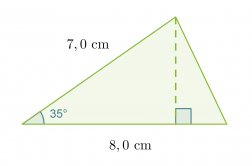
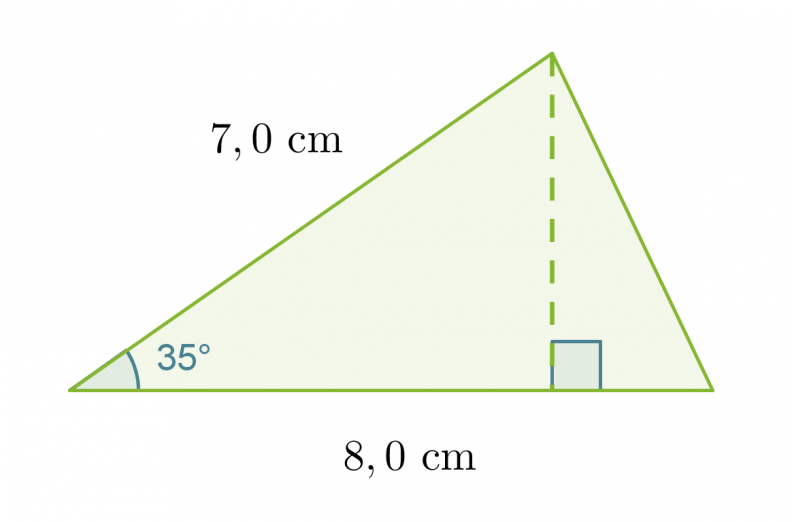
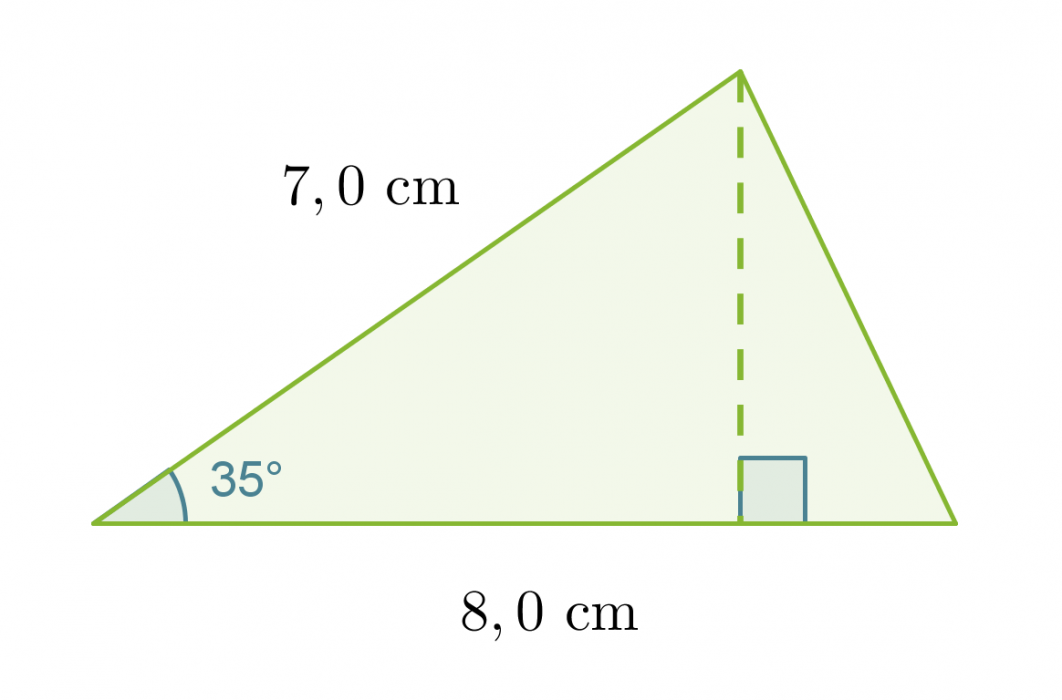
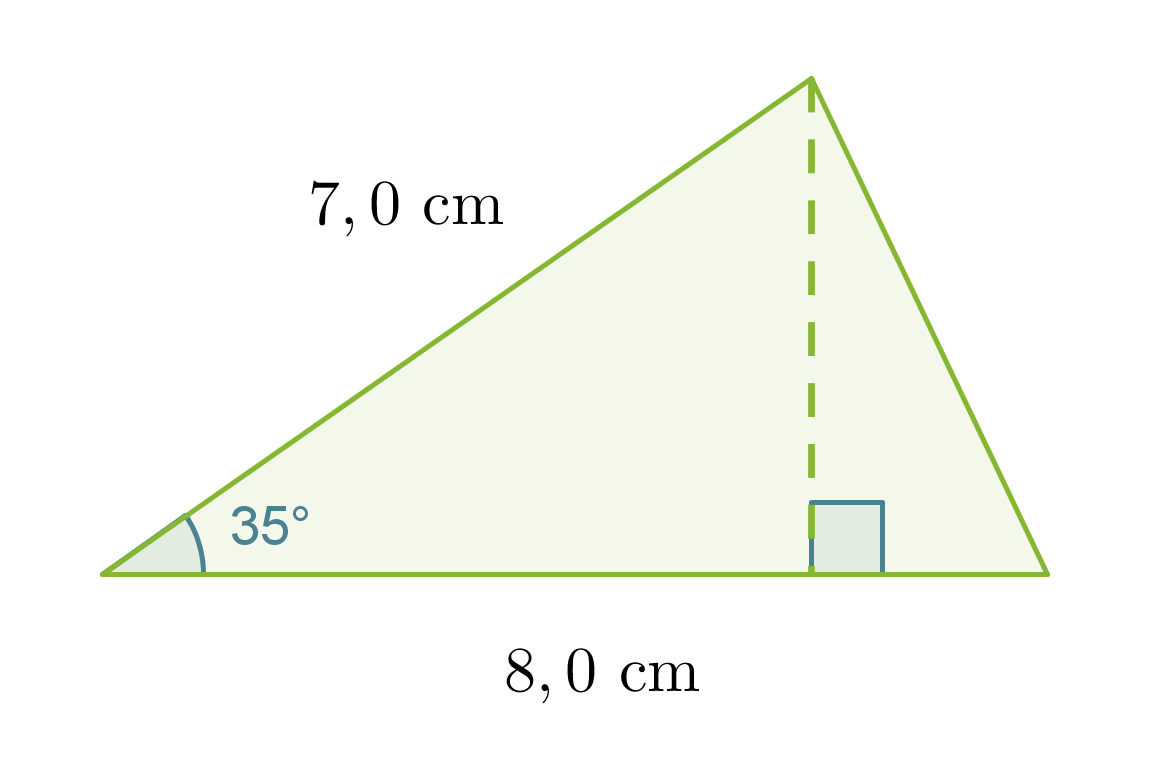
Esimerkki 1.
Lasketaan viereisen kolmion pinta-ala.
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
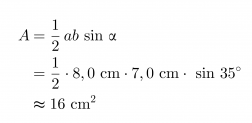
Klikkaa kuva suuremmaksi!
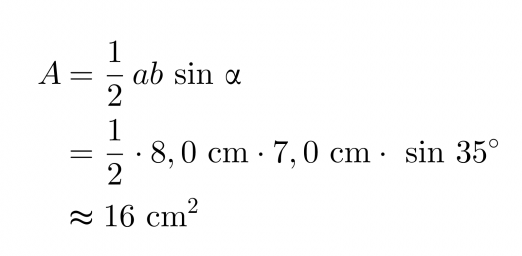
Klikkaa kuva suuremmaksi!
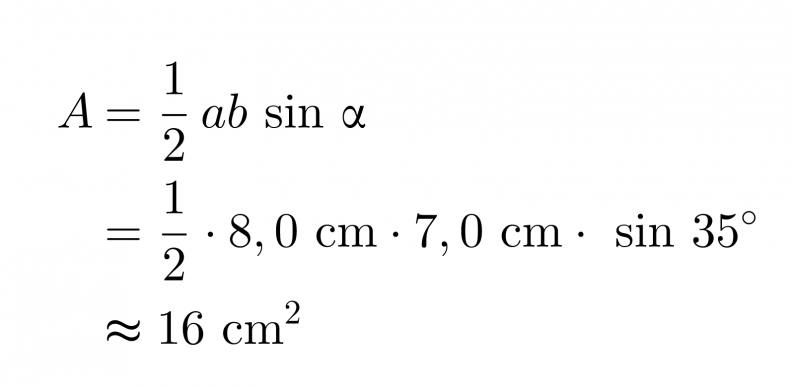
Klikkaa kuva suuremmaksi!
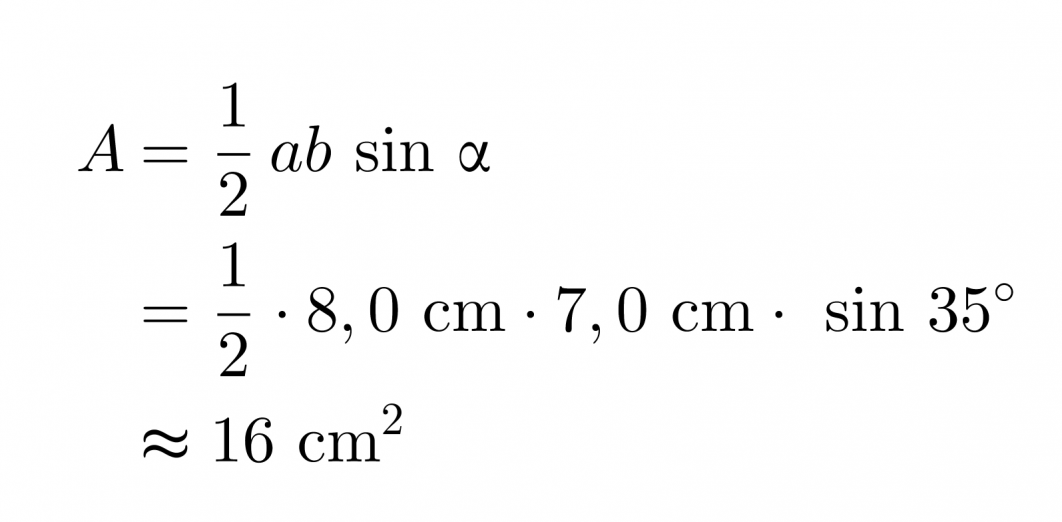
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Kolmion pinta-ala on 16 cm2.
Esimerkki 2.
Kolmion sivujen pituudet ovat 6,2 cm ja 8,5 cm. Kuinka suuri on sivujen välinen kulma, kun kolmion pinta-ala on 24,8 cm2?
Ratkaisu:
Määritetään ensin sivujen välisen kulman sini:
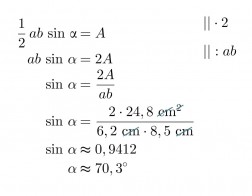
Klikkaa kuva suuremmaksi!
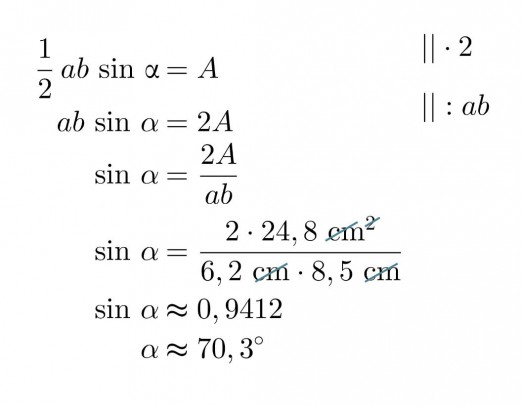
Klikkaa kuva suuremmaksi!
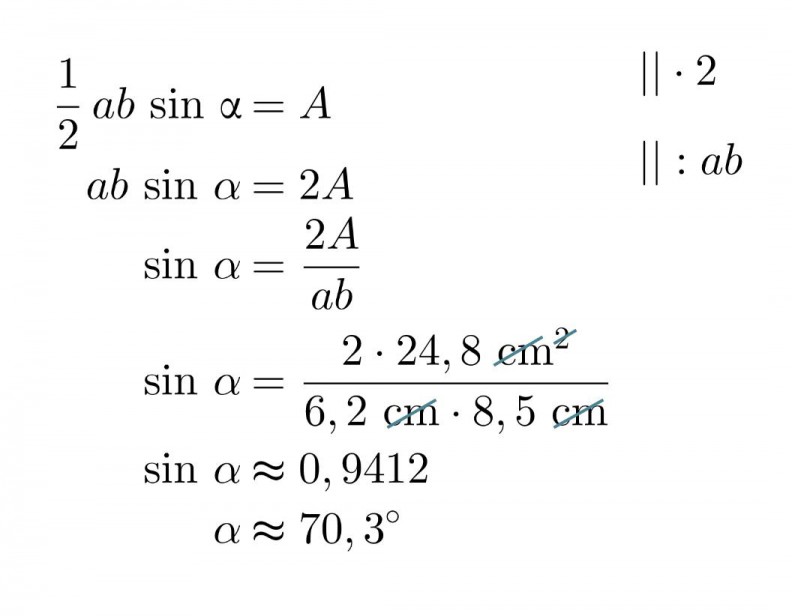
Klikkaa kuva suuremmaksi!
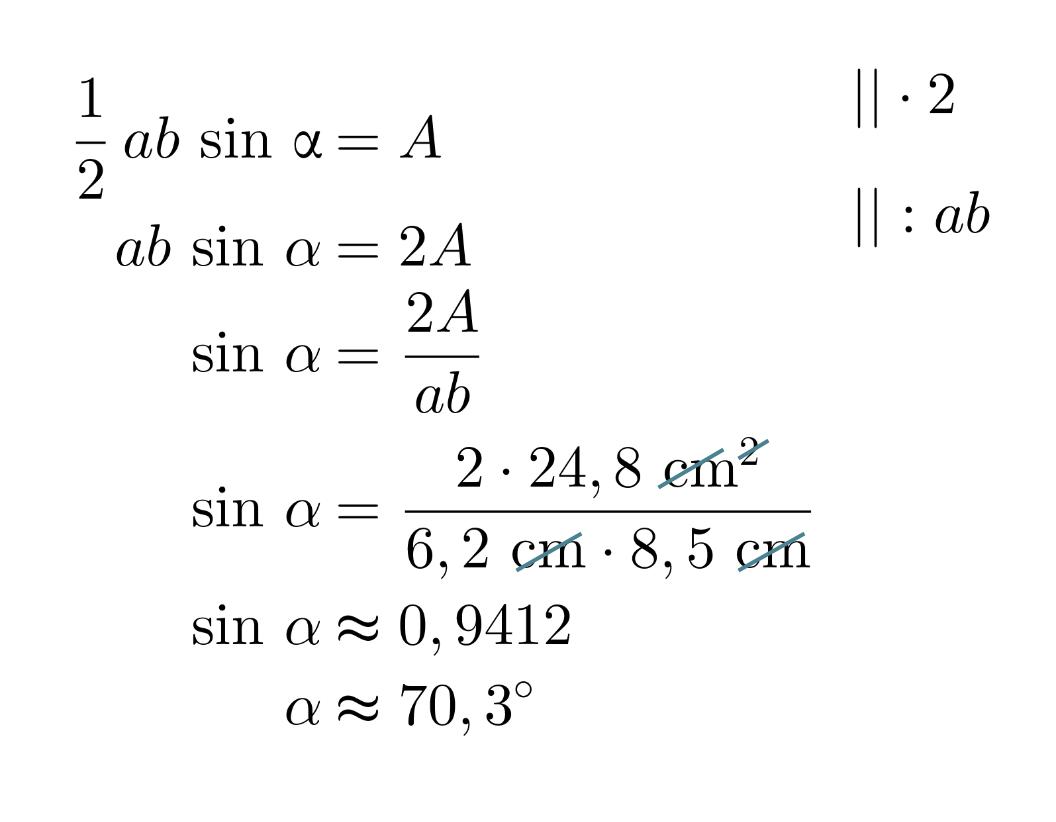
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Laskimella saadaan yhtälön toteuttava terävä kulma. Yhtälöllä on kuitenkin myös toinen ratkaisu, joka on 180° − 70,3° = 109,7°.
Laskimella voidaan vielä tarkistaa, että 180° − 70,3° = 109,7°.
Vastaus: Kulma on 70,3° tai 109,7°.
Yleisesti pätee seuraava sääntö:
sin α = sin(180° − α)