10. Lieriön tilavuus
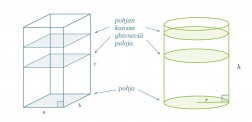
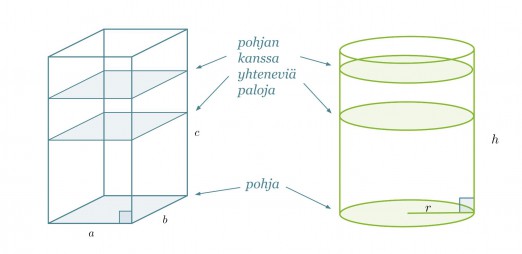
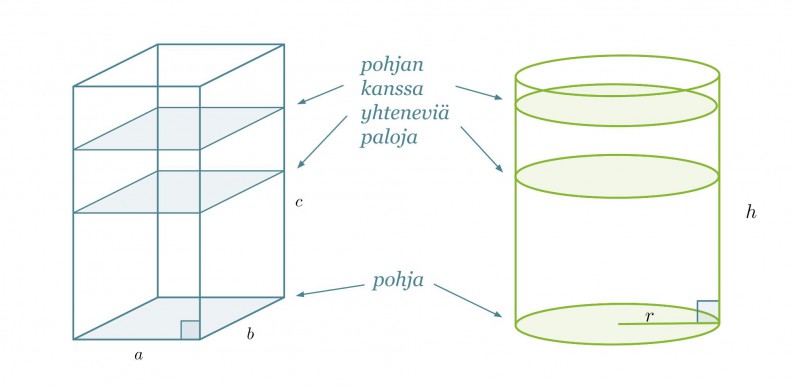
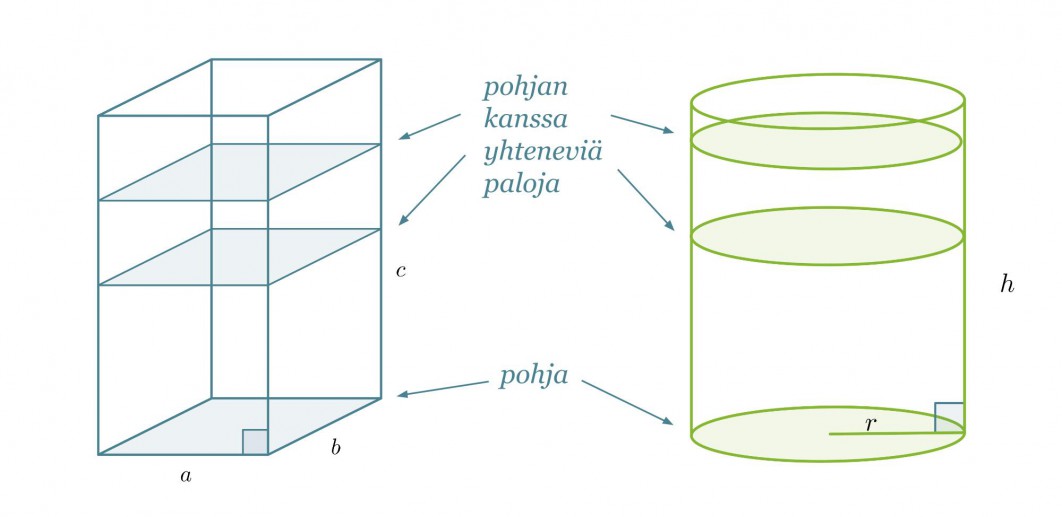
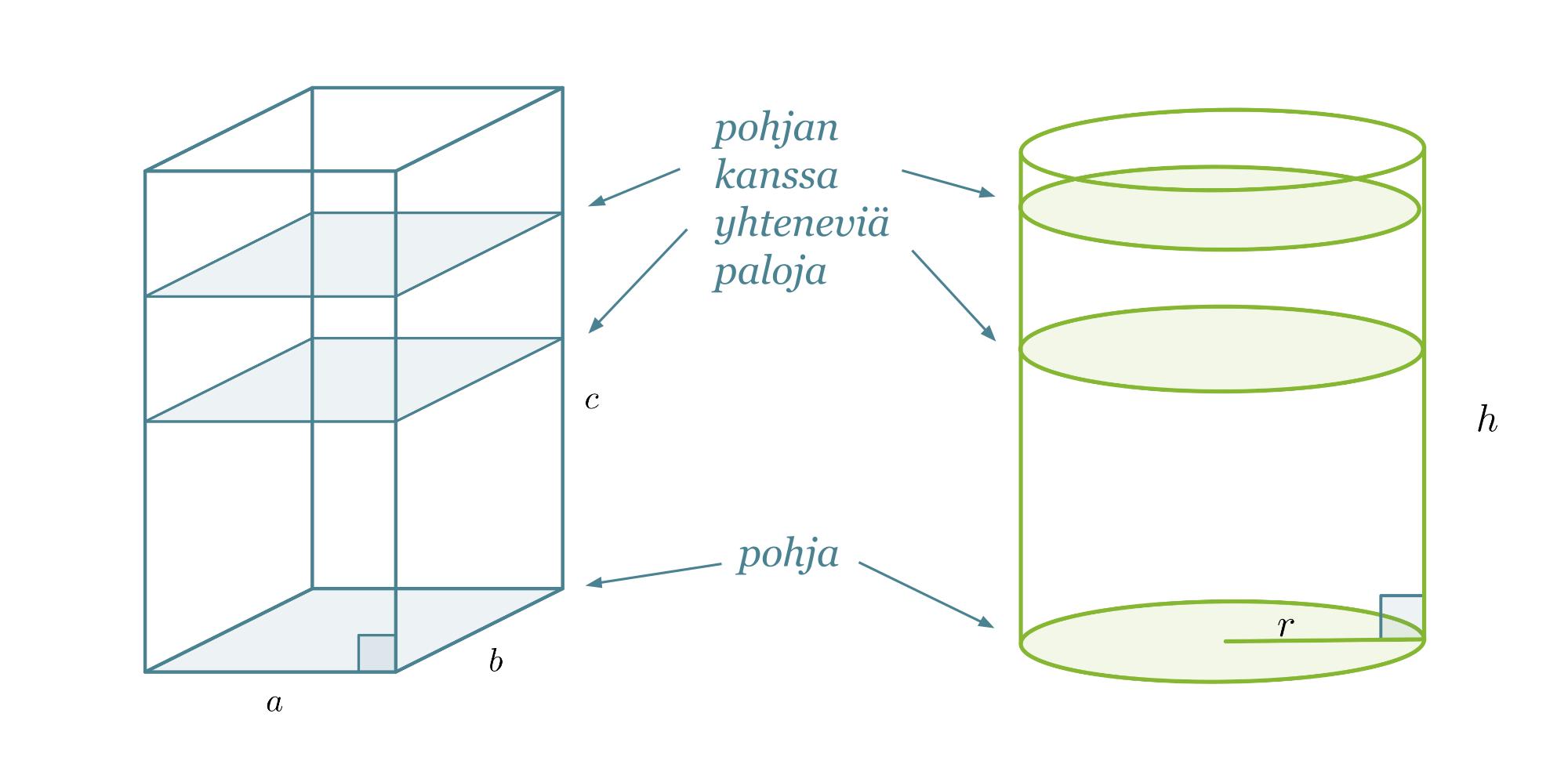
Tarkastellaan suorakulmaisen särmiön ja suoran ympyrälieriön muotoisia kappaleita. Kappaleen tilavuuden voidaan ajatella muodostuvan siten, että täytetään kappale pohjan kanssa yhtenevillä paloilla.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Mittaustarkkuuden, jolla kappaleiden korkeudet (tässä c ja h) on annettu, voidaan ajatella muodostuvan pudotettujen palojen paksuudesta. Jos korkeus on annettu senttimetrin tarkkuudella, ovat palat paksuudeltaan yhden senttimetrin.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
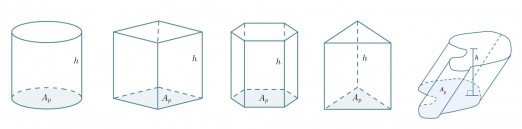
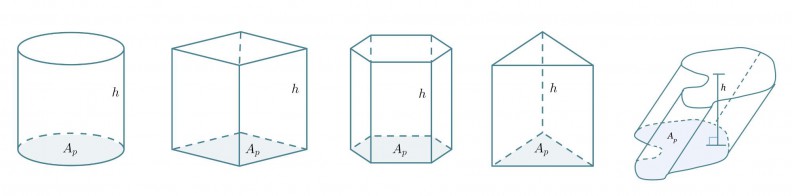
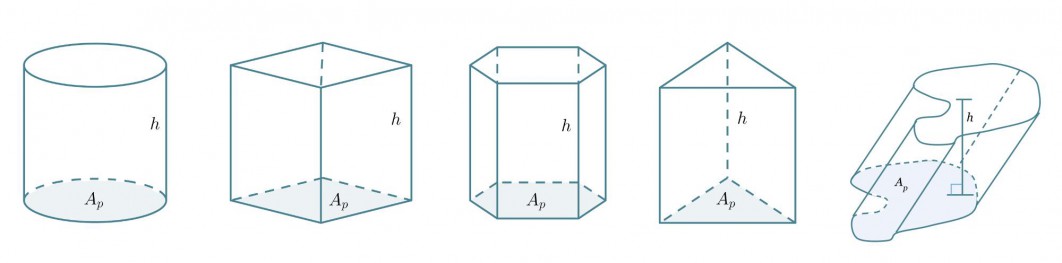
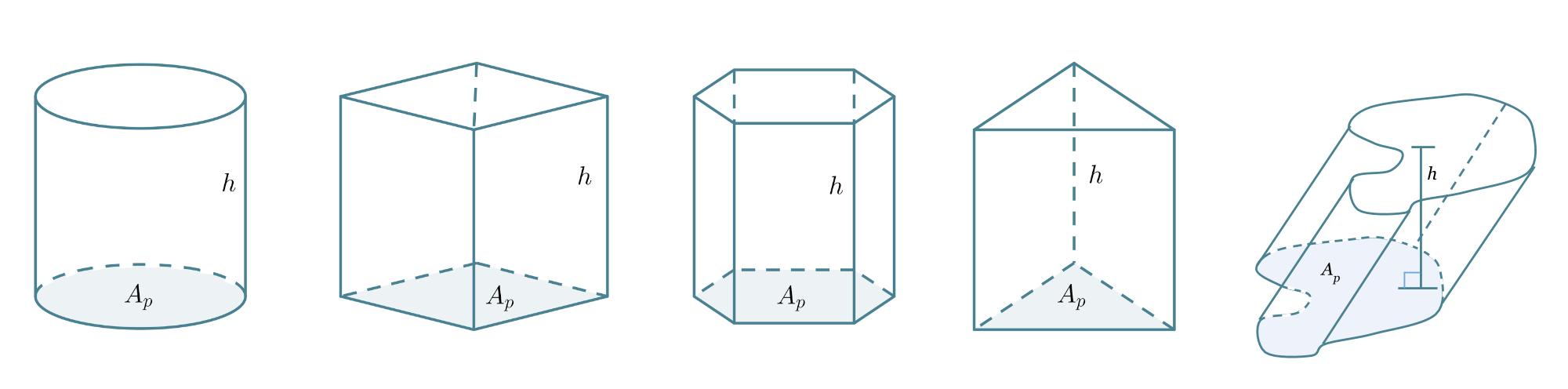
Riippumatta lieriön pohjan muodosta tai siitä onko kyseessä suora vai vino lieriö lasketaan sen tilavuus samalla tavalla.
Lieriön tilavuus saadaan pohjan pinta-alan Ap ja korkeuden h tulona.
V = Ap h
Huom! Jos lieriö on vino, on korkeus lieriön kannen kohtisuoraan mitattu etäisyys pohjasta.
Esimerkki 1.
Lasketaan Italiassa sijaitsevan Pisan kaltevan tornin tilavuus.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Oletetaan tornin olevan kauttaaltaan saman levyinen. Pohjan halkaisija on 15,5 m ja tornin korkeus 55,9 m.
Torni on muodoltaan ympyrälieriö, jonka pohjan pinta-ala on Ap = πr2 ja korkeus h, joten tilavuus saadaan lasketuksi kaavalla V = πr2h.
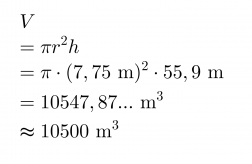
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
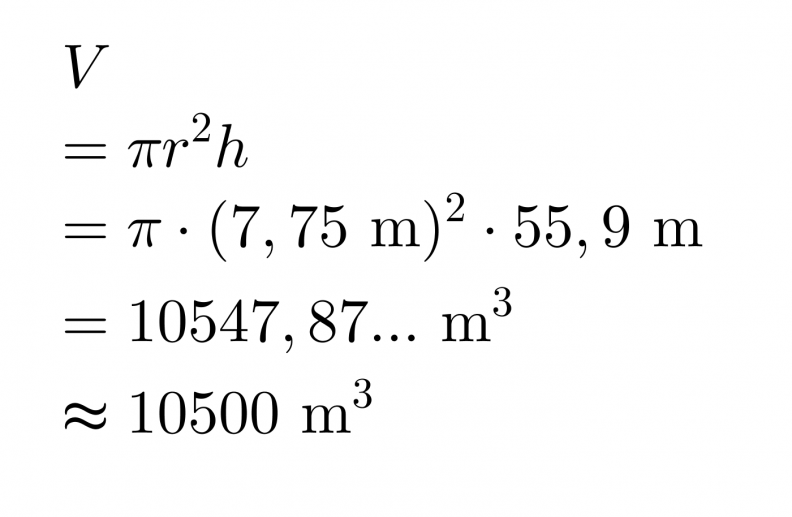
Klikkaa kuva suuremmaksi!
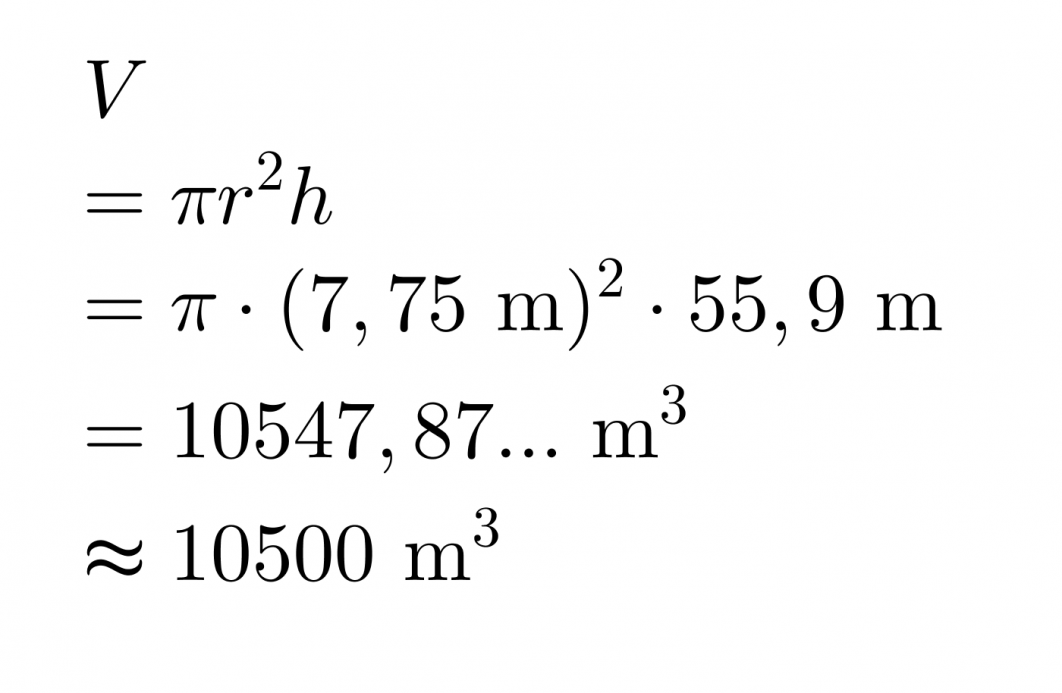
Klikkaa kuva suuremmaksi!
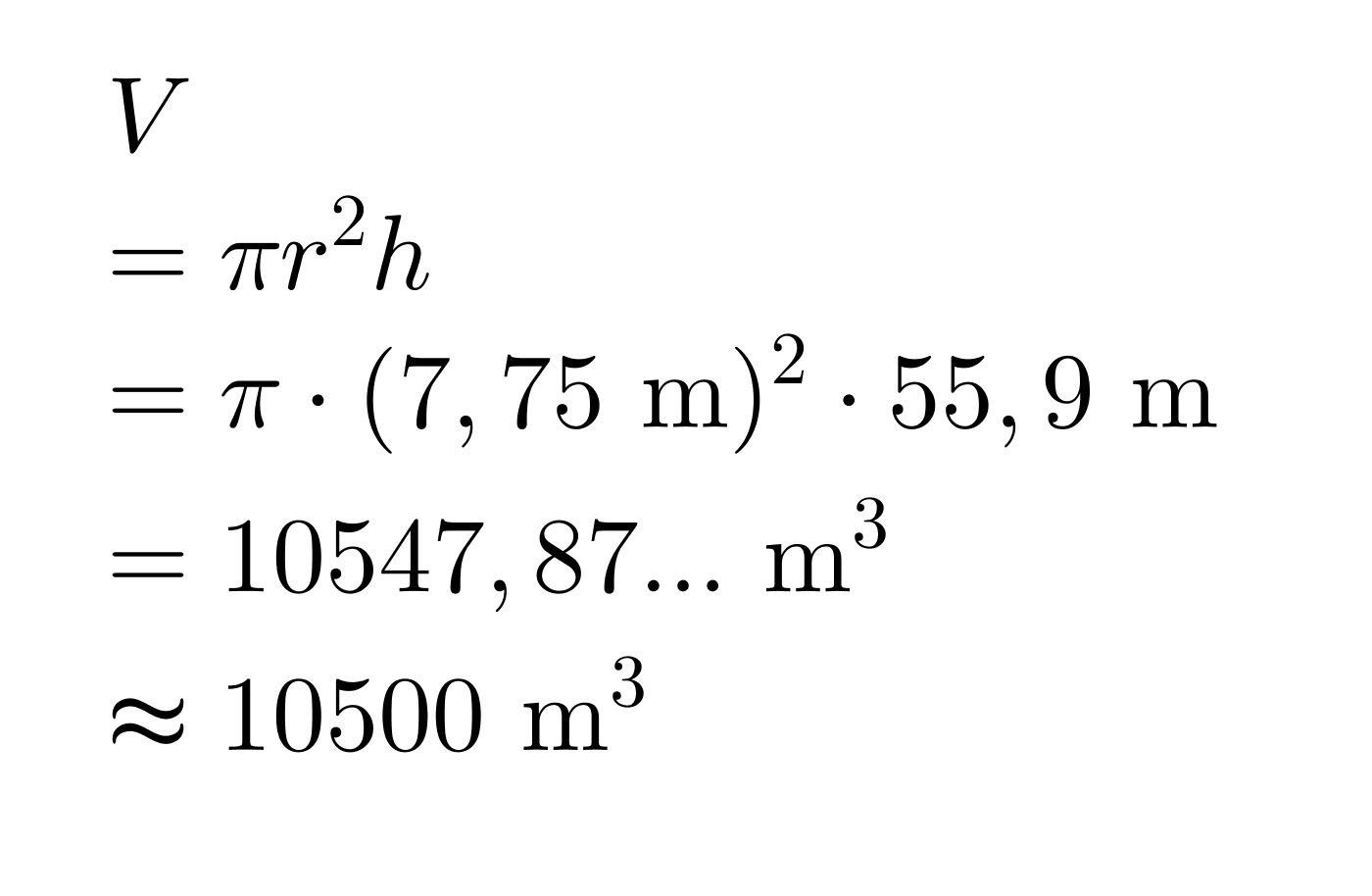
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Pisan kaltevan tornin tilavuus on 10500 m3.
Jos laskussa olisi haluttu olla tarkkoja, mikä olisi pitänyt ottaa huomioon?
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014