11. Kartion tilavuus
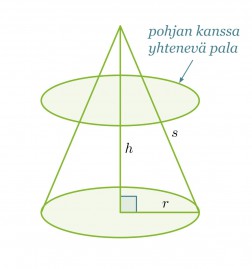
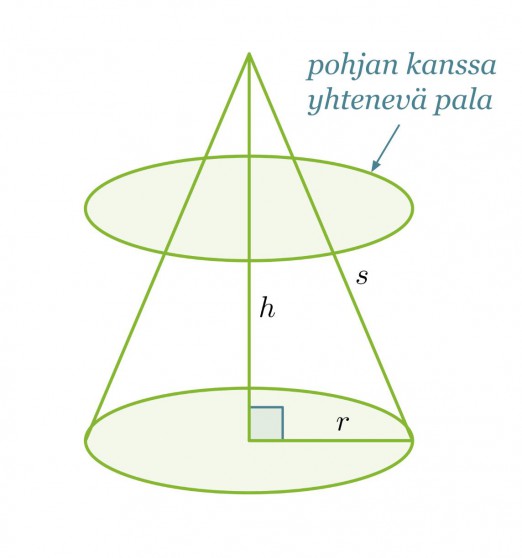
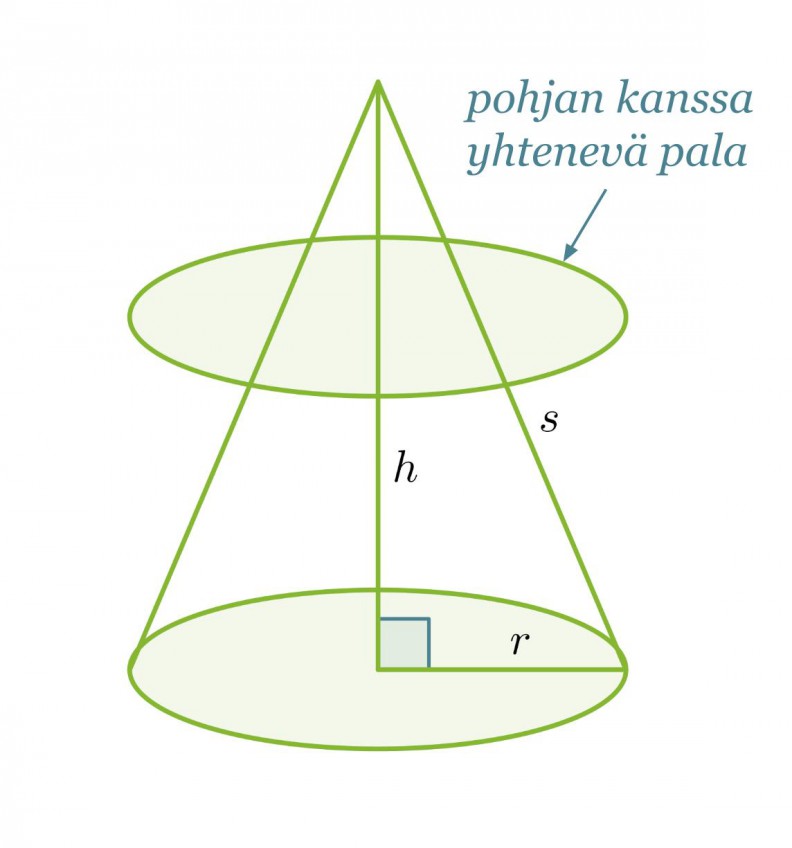
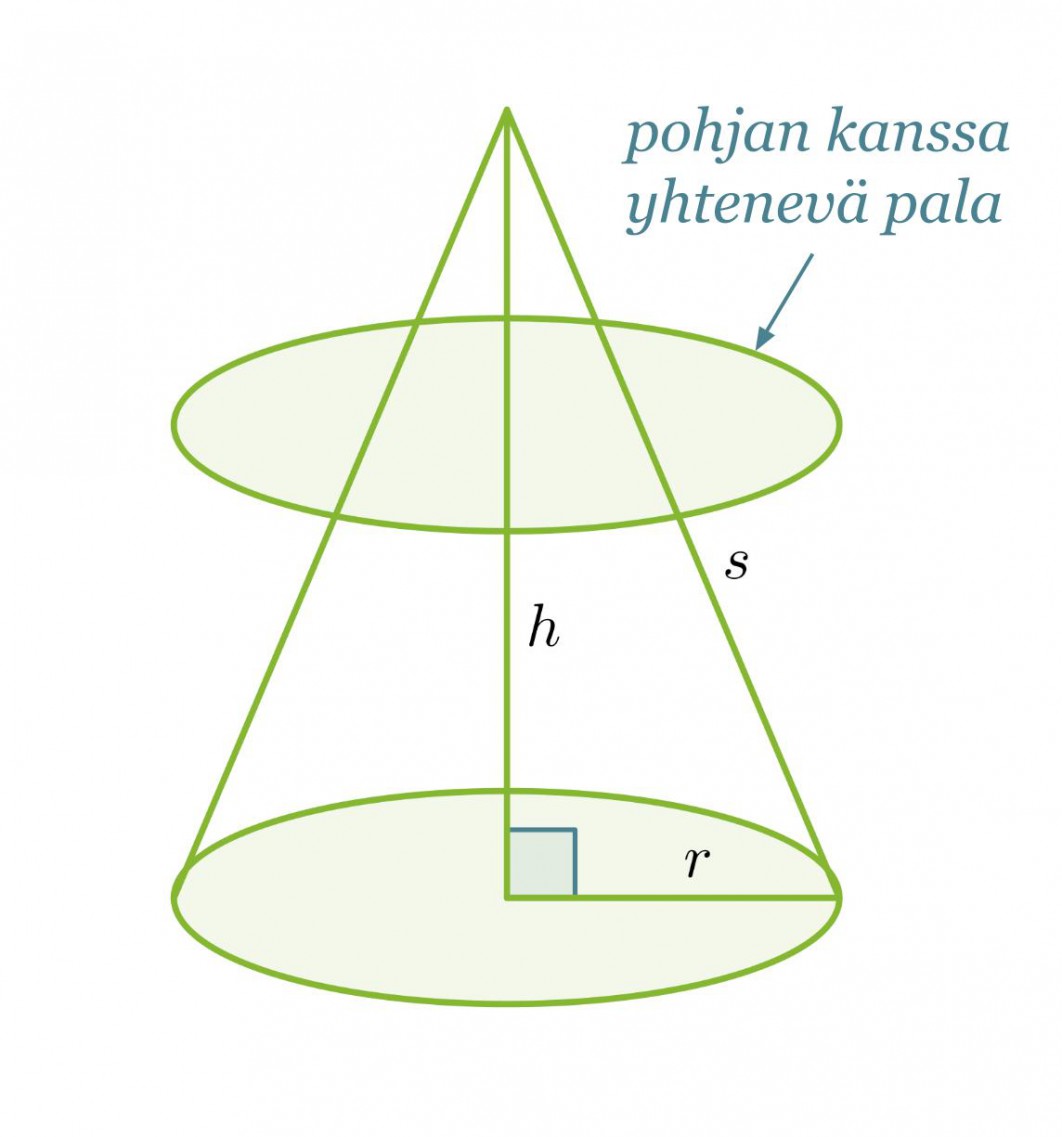
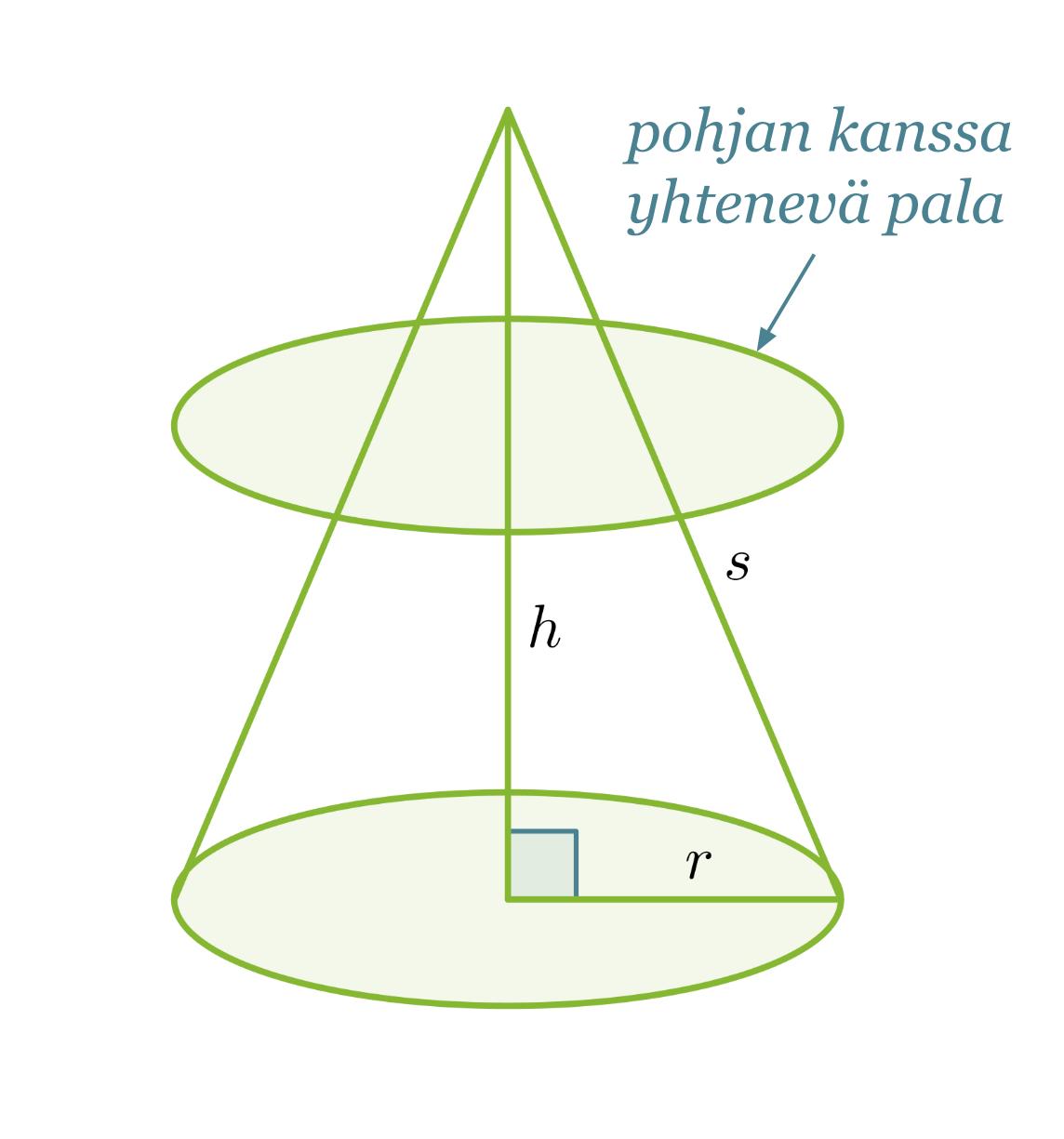
Ympyräkartion tilavuutta ei saada laskettua täyttämällä sitä pohjan kanssa yhtenevillä paloilla. Tällöinhän laskettaisiin ympyrälieriön tilavuutta.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
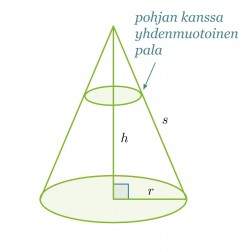
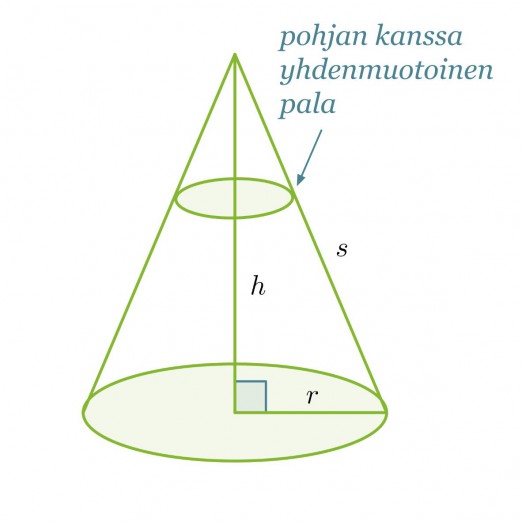
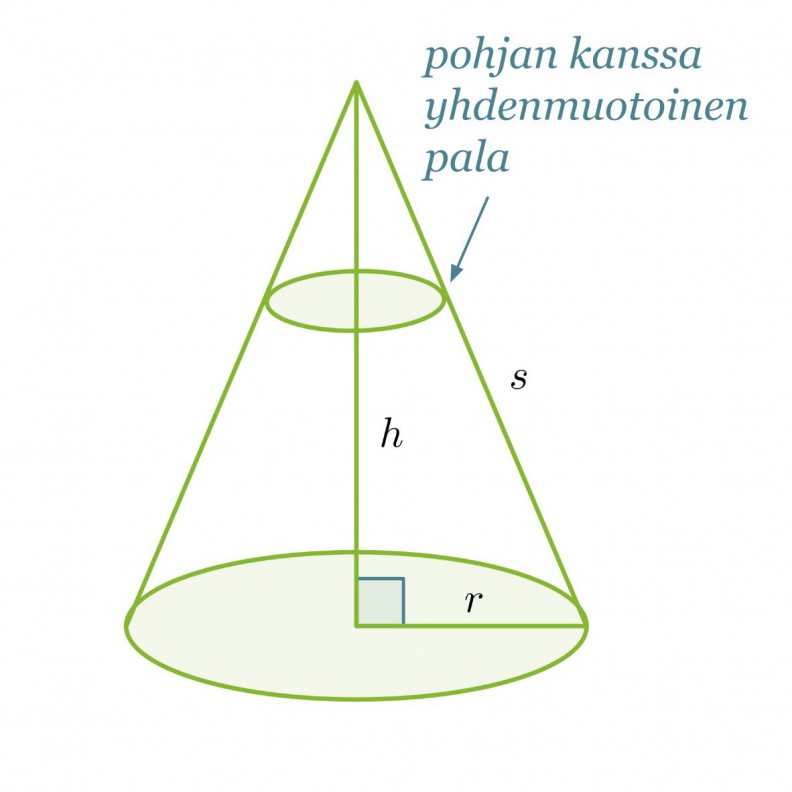
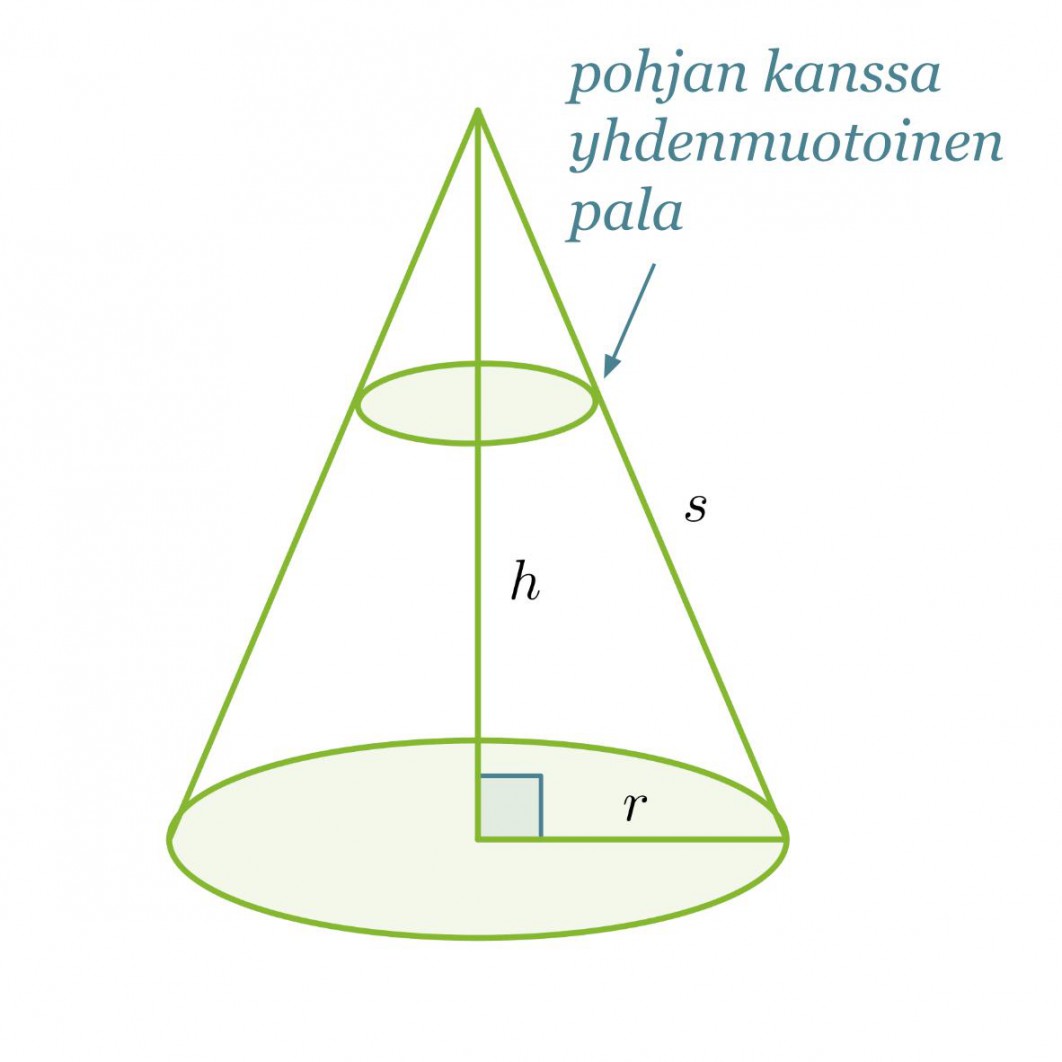
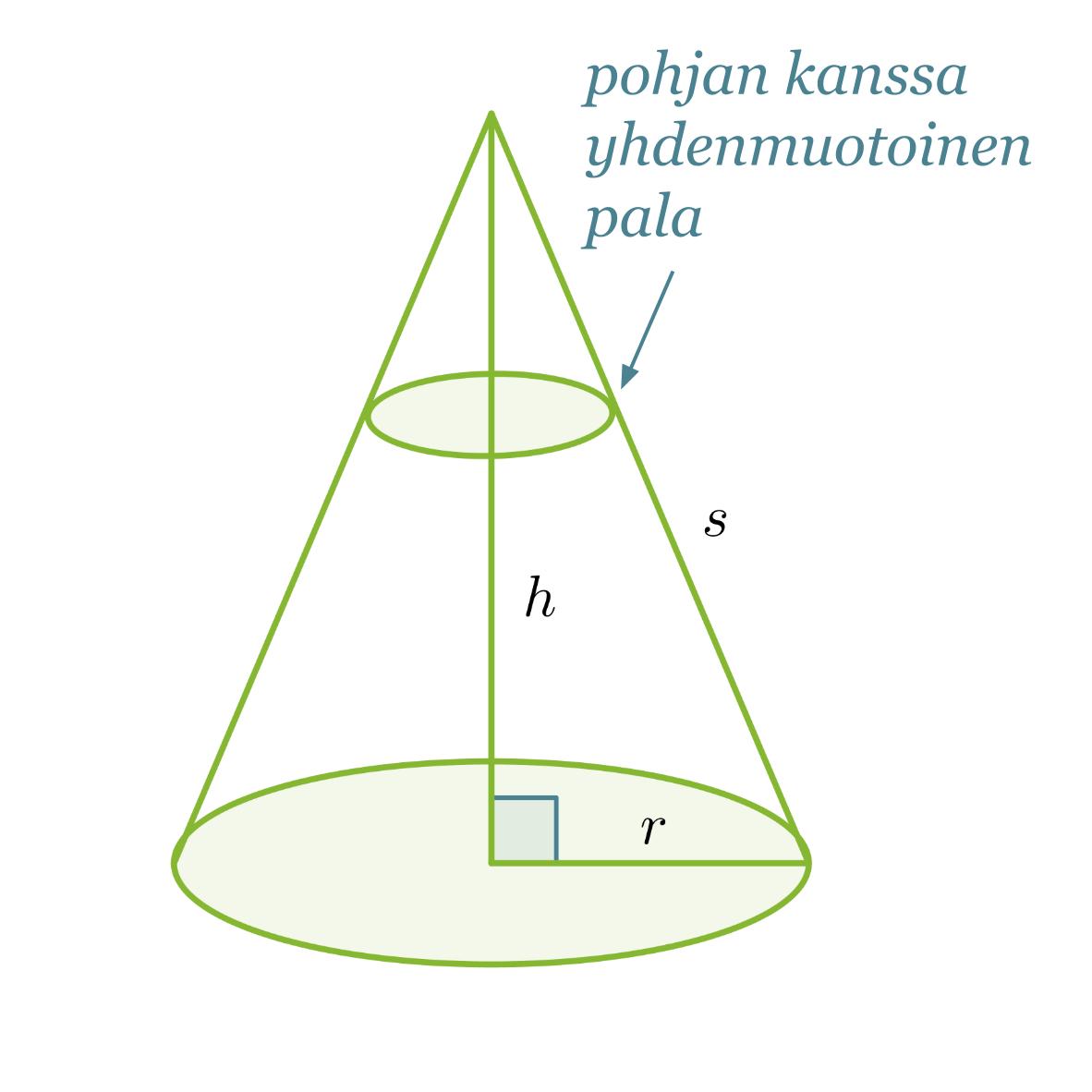
Ympyräkartion tilavuus sitä vastoin saadaan täyttämällä se pohjan kanssa yhdenmuotoisilla paloilla, jotka pienenevät kartion kärkeä kohti mentäessä. Koska yhdenmuotoisten kappaleiden välillä vallitsee suhde, voimme olettaa kartion tilavuuden saatavan seuraavasti:
kartion tilavuus = jokin suhdeluku · vastaavan lieriön tilavuus.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
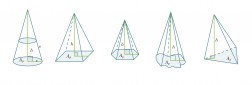
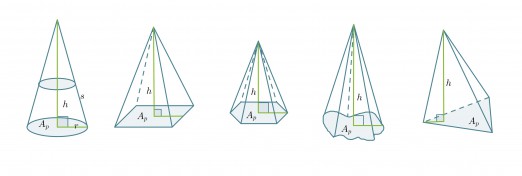
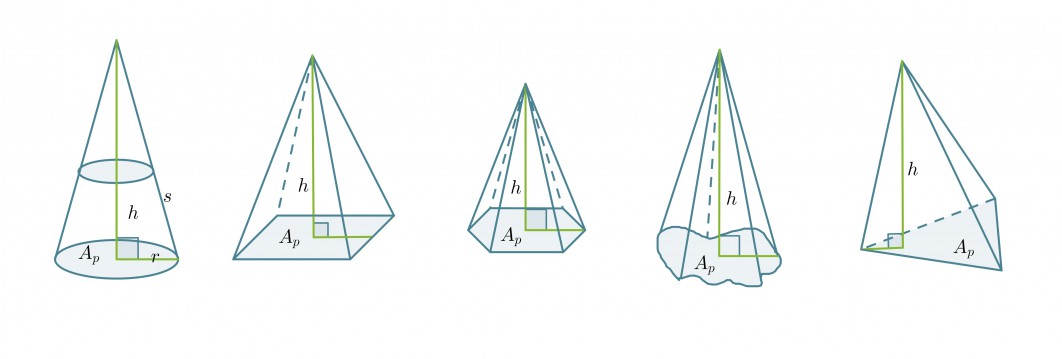
Riippumatta kartion pohjan muodosta lasketaan sen tilavuus aina samalla tavalla. Pohjan muoto tulee huomioitua sen pinta-alan kaavassa.
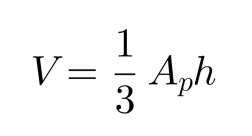
Klikkaa kuva suuremmaksi!
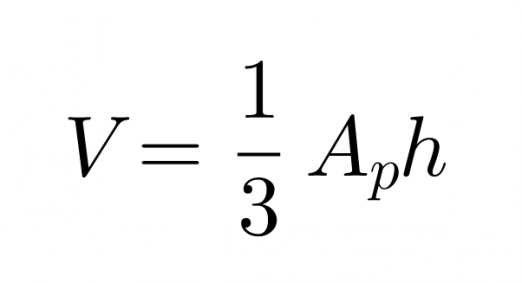
Klikkaa kuva suuremmaksi!
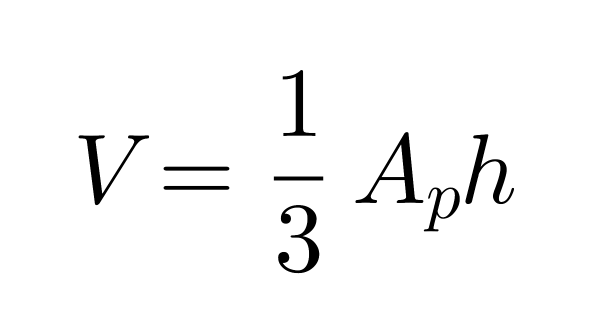
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
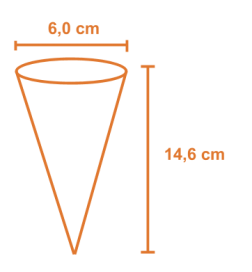
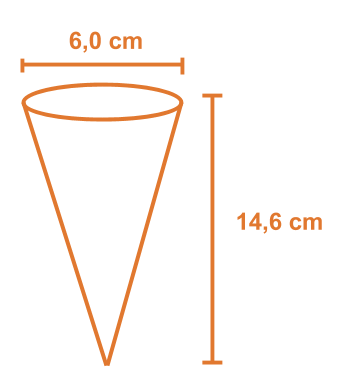
Lasketaan jäätelötuutin tilavuus.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jäätelötuutti on muodoltaan ympyräkartio, jonka pohjan pinta-ala lasketaan säteen r avulla seuraavasti Ap = πr2. Kartion tilavuuden laskukaava tulee siten muotoon
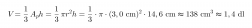
Klikkaa kuva suuremmaksi!
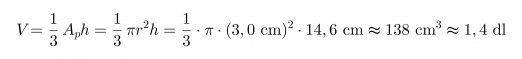
Klikkaa kuva suuremmaksi!
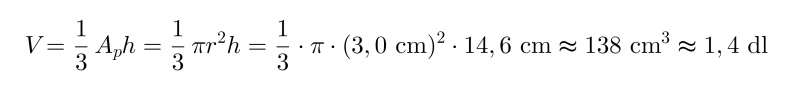
Klikkaa kuva suuremmaksi!
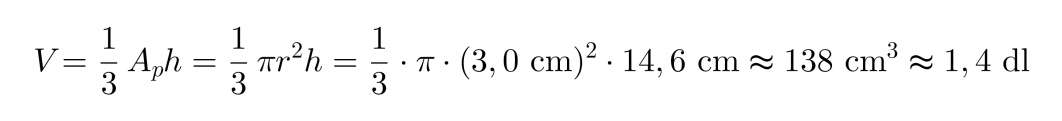
Klikkaa kuva suuremmaksi!
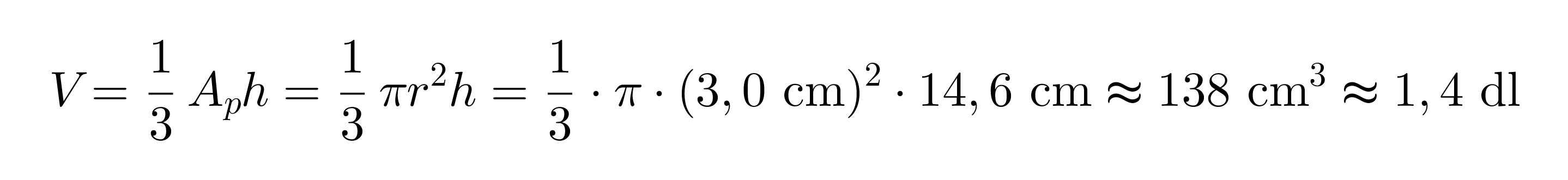
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Tuutin tilavuus on noin 1,4 dl.
Esimerkki 2.
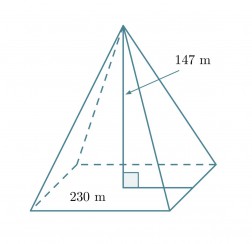
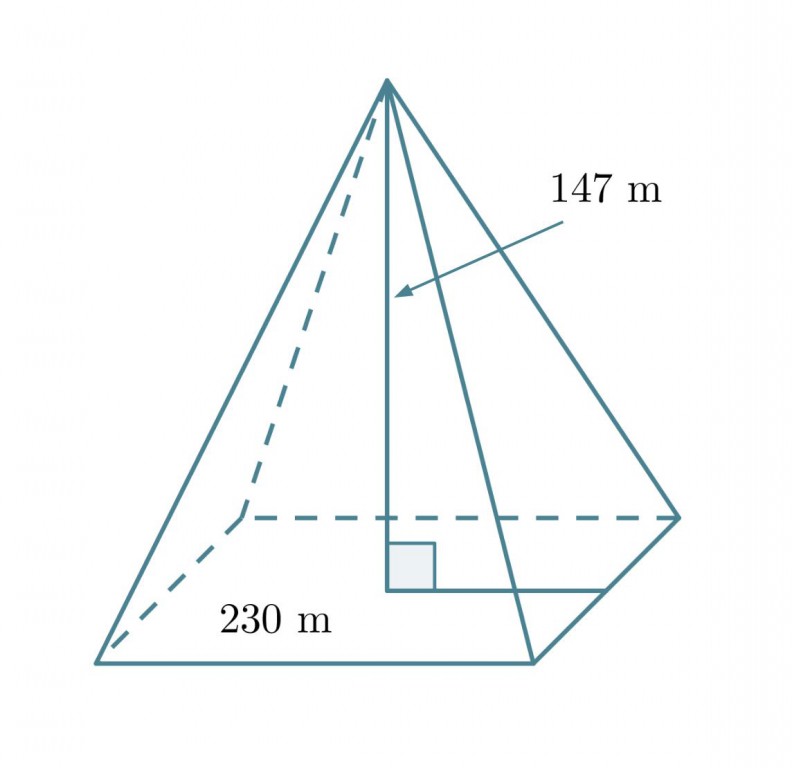
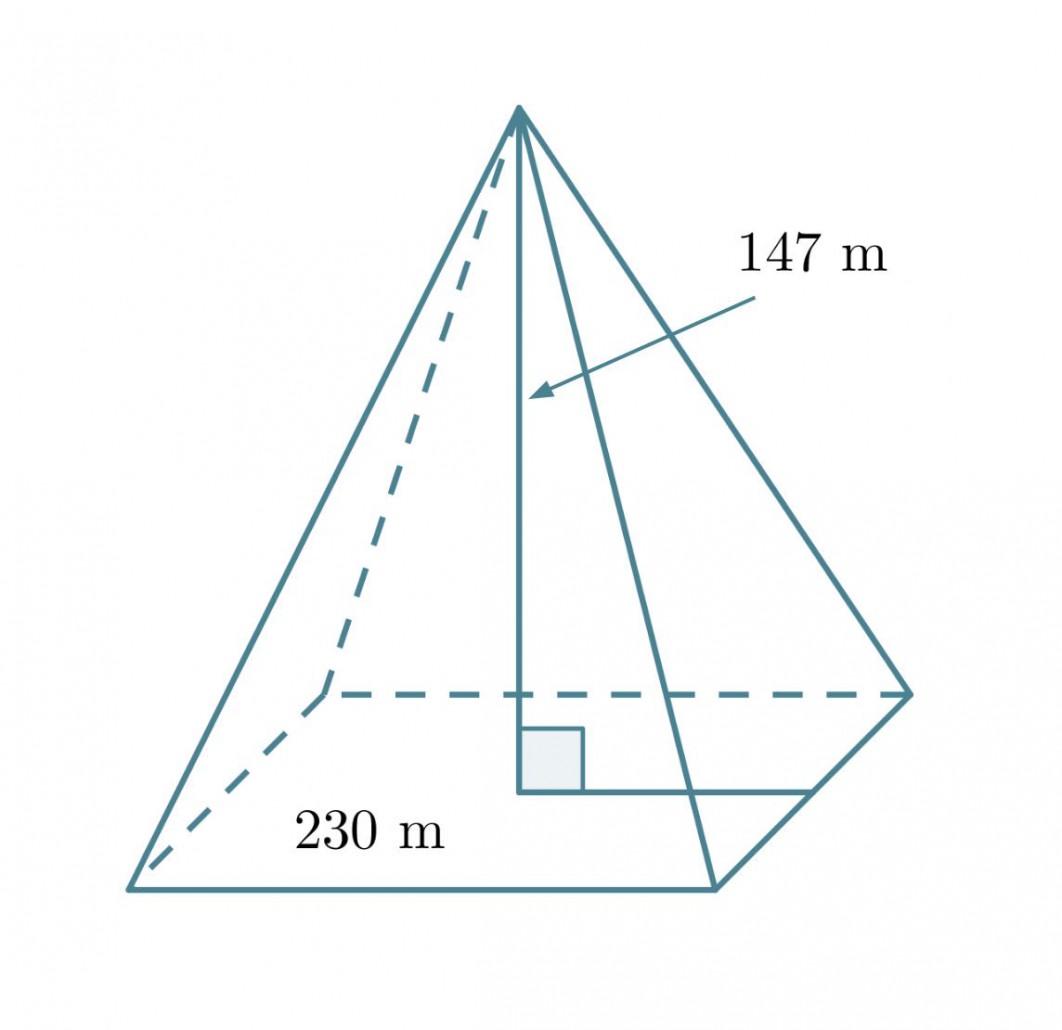
Kheopsin pyramidi oli alunperin 147 m korkea ja sen pohjasärmän pituus oli 230 m. Lasketaan pyramidin tilavuus.
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Pyramidi on kartion erikoistapaus ja sen tilavuus saadaan samojen laskusääntöjen mukaisesti. Pyramidin pohja muodostuu neliöstä, jonka pinta-ala saadaan neliön särmän s avulla seuraavasti Ap = s2. Pyramidin tilavuus on
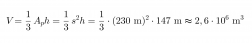
Klikkaa kuva suuremmaksi!
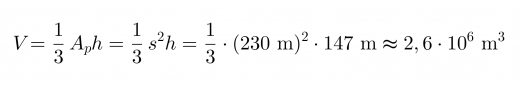
Klikkaa kuva suuremmaksi!
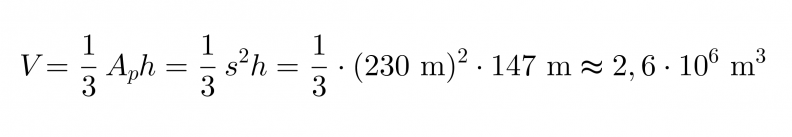
Klikkaa kuva suuremmaksi!
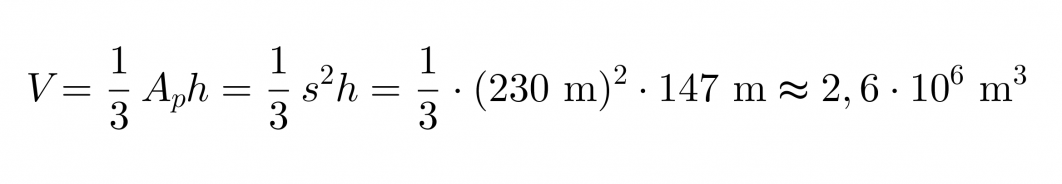
Klikkaa kuva suuremmaksi!
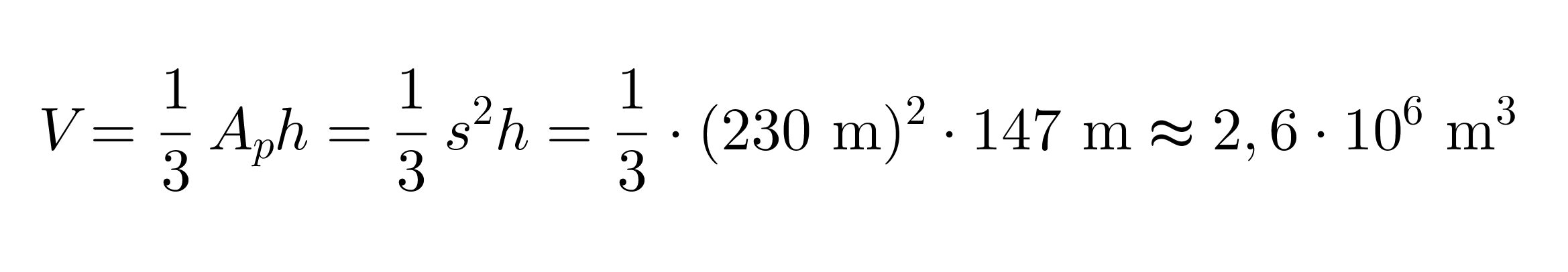
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Kheopsin pyramidin tilavuus oli alunperin 2,6 · 106 m3.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014
Kartion tilavuus
Kartion tilavuus on 1/3 sellaisen lieriön tilavuudesta, jonka pohjan pinta-ala Ap ja korkeus h ovat samat kuin kartiolla.