13. Monitahokkaat
Monitahokkaat ovat aukottomia kappaleita, jotka muodostuvat monikulmioista.
Monikulmioita sanotaan monitahokkaan tahkoiksi. Säännöllisen monitahokkaan rajapintoina voi olla myös useita erilaisia säännöllisiä monikulmioita. Ns. Arkhimedeen kappaleissa ylä- ja alapintana on jokin säännöllinen monikulmio ja sivut muodostuvat neliöistä. Jos yksinkertaiset särmiöt jätetään pois laskuista, on erilaisia Arkhimedeen kappaleita 13.
Kaikkien monitahokkaiden kärkien k, tahkojen t ja särmien s lukumäärien välillä pätee Eulerin kaava
k + t = s + 2.
Platonin kappaleet ovat säännöllisiä monitahokkaita, joiden kaikki sivutahkot ovat yhteneviä säännöllisiä monikulmioita.
Platonin kappaleita on olemassa ainoastaan viisi. Tunnetuin näistä on neliöistä muodostuva kuutio eli heksaedri. Kolmioista muodostuvat Platonin kappaleet ovat tetraedri (4-tahokas), oktaedri (8-tahokas) ja Ikosaedri (20-tahokas).

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Dodekaedri (12-tahokas) muodostuu viisikulmioista.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
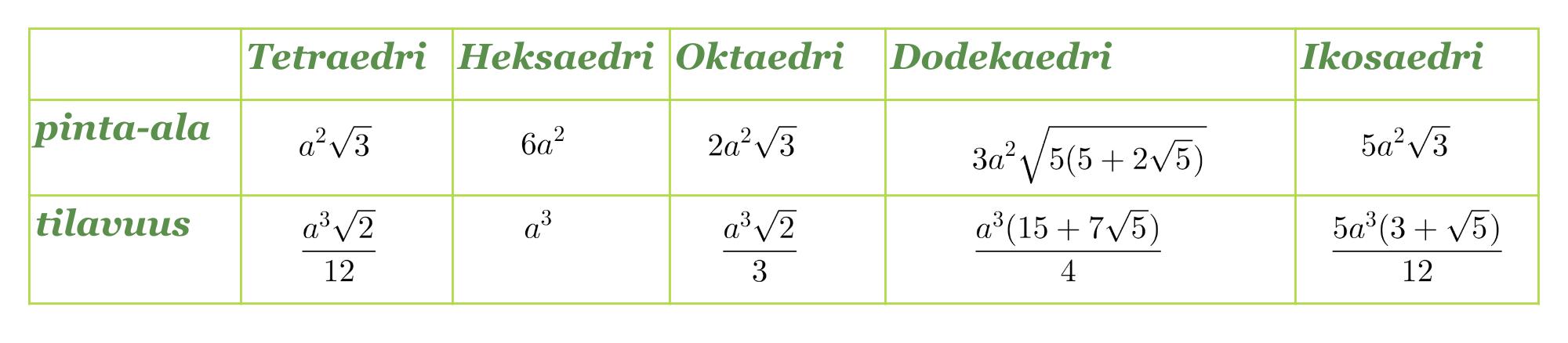
Jos säännöllisten monitahokkaiden särmä on a, saadaan kappaleiden pinta-alat ja tilavuudet lasketuksi oheisen taulukon kaavoilla.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
Mausteseos on pakattu tetraedrin muotoiseen pakkaukseen, jonka särmän pituus on 3,8 cm. Lasketaan pakkauksen
a) Pinta-ala
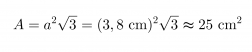
Klikkaa kuva suuremmaksi!
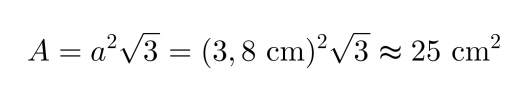
Klikkaa kuva suuremmaksi!
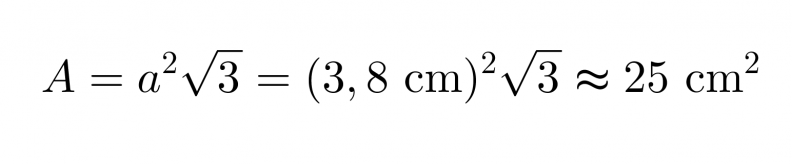
Klikkaa kuva suuremmaksi!
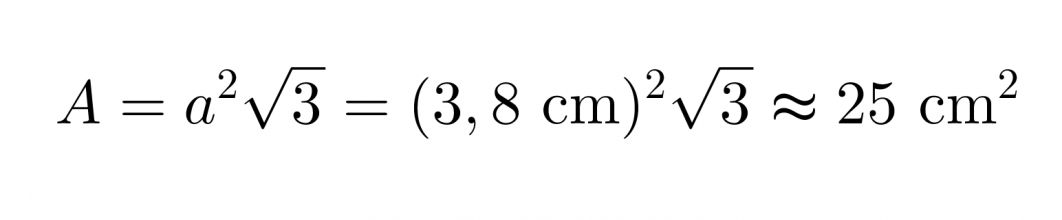
Klikkaa kuva suuremmaksi!
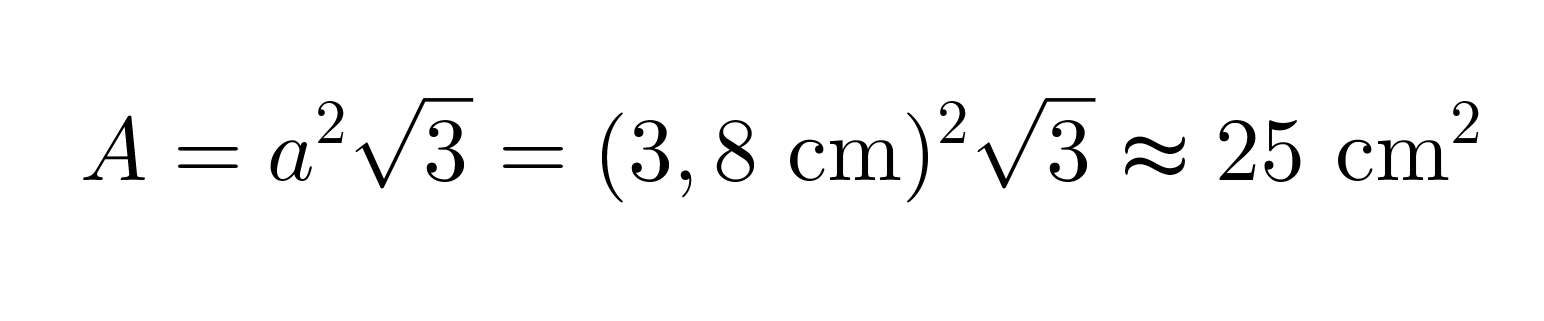
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
b) tilavuus
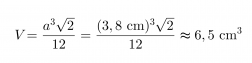
Klikkaa kuva suuremmaksi!
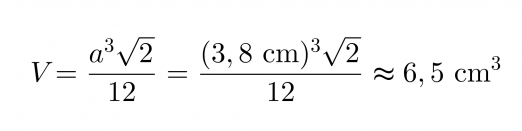
Klikkaa kuva suuremmaksi!
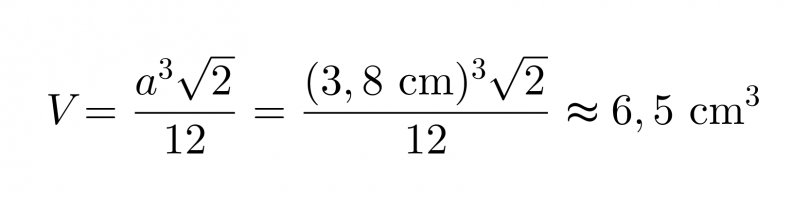
Klikkaa kuva suuremmaksi!
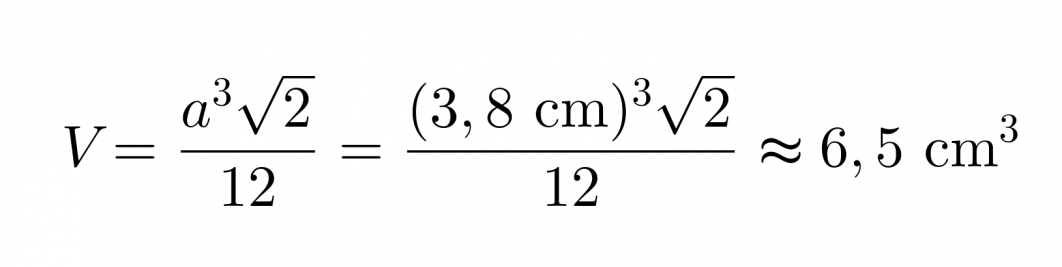
Klikkaa kuva suuremmaksi!
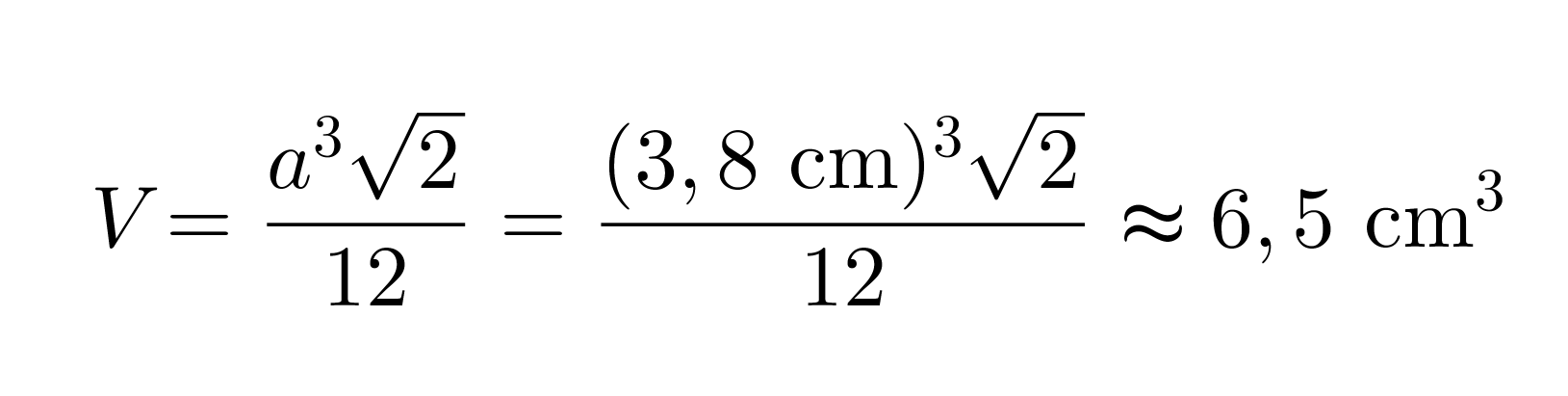
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Pakkauksen pinta-ala on 25 cm2 ja tilavuus on 6,5 cm3.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014