15. Yhdenmuotoisten kappaleiden pinta-alat ja tilavuudet
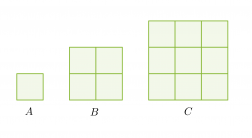
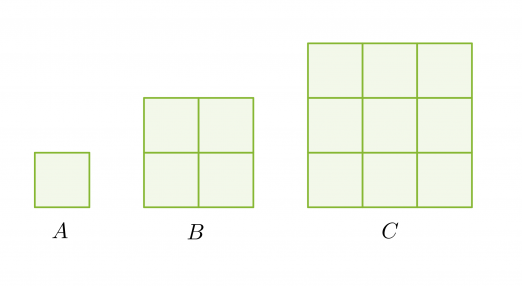
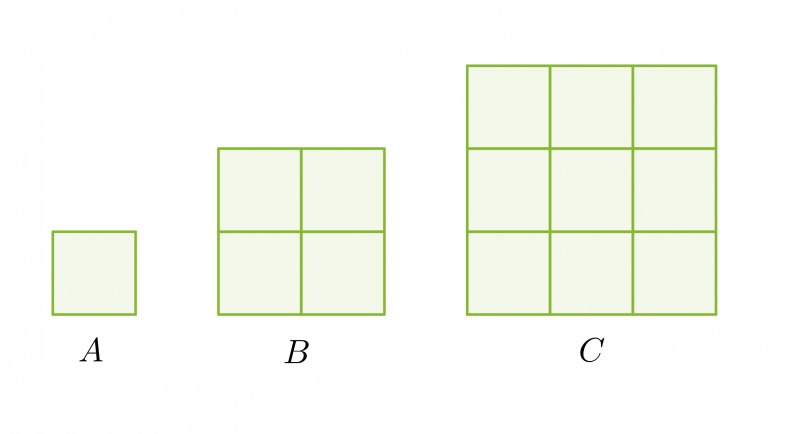
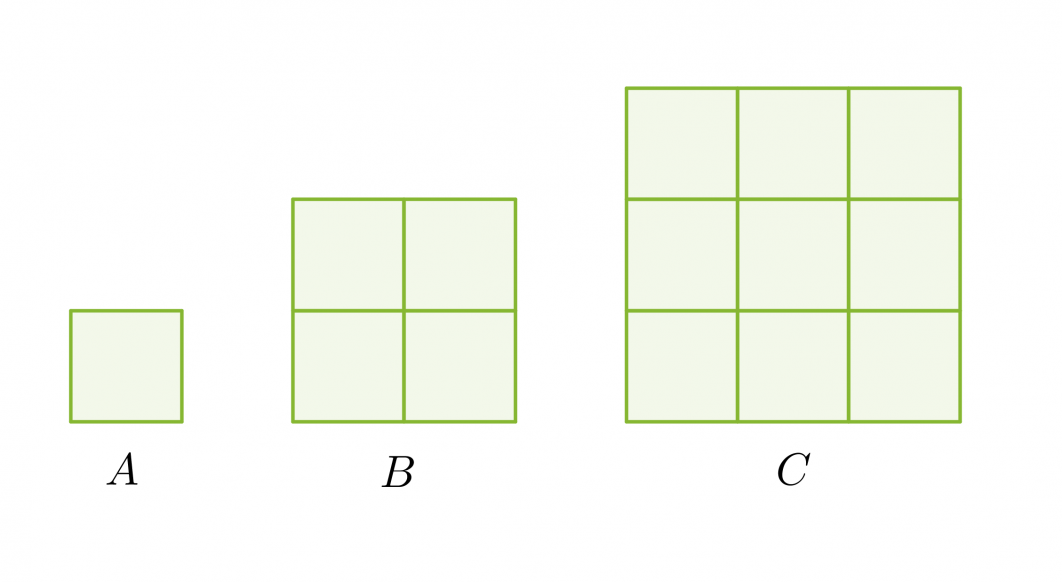
Kolme neliötä on muodostettu yhdenmuotoisista kuvioista. Sivujen pituuksien suhde on 1 : 2 : 3 ja pinta-alojen suhde 1 : 4 : 9.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
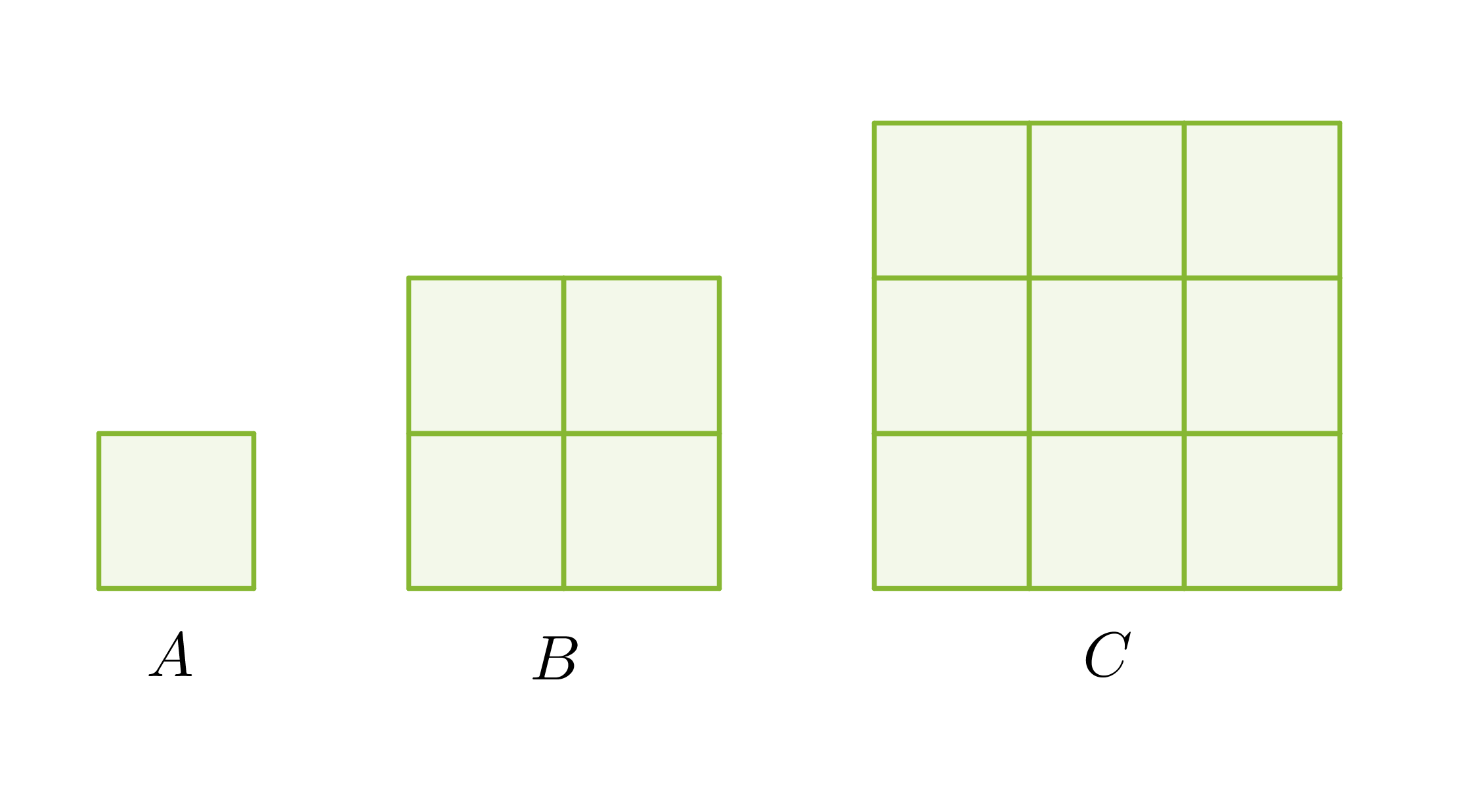
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Pituuksien ja pinta-alojen suhteiden välillä on yhteys. Pinta-alojen suhteet voidaan kirjoittaa pituuksien suhteiden avulla seuraavasti: 12 : 22 : 32.
Yhdenmuotoisten kuvioiden pinta-alojen suhde on verrannollinen pituuksien suhteiden neliöön.
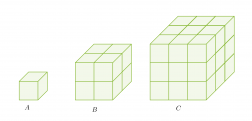
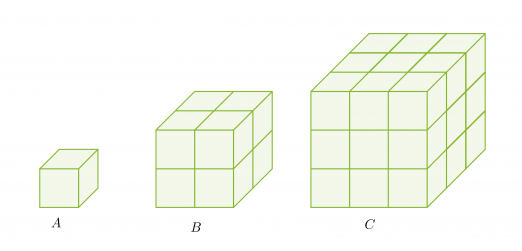
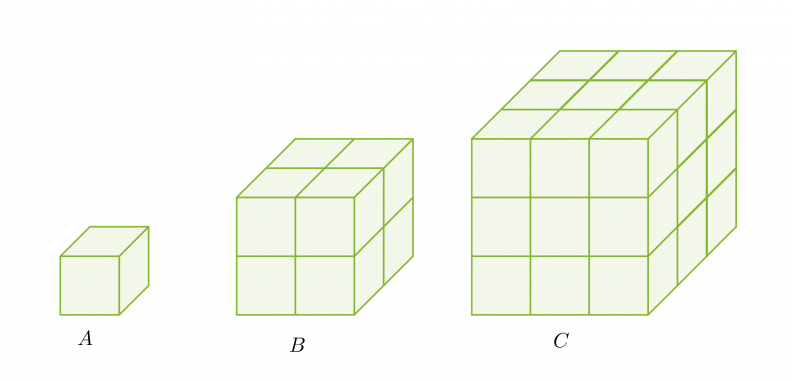
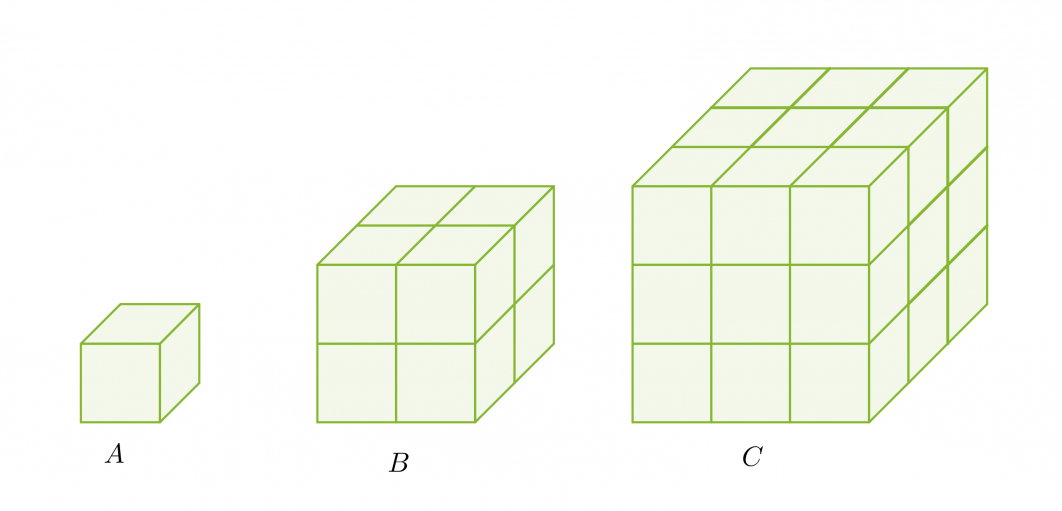
Yhdenmuotoisuus avaruudessa määritellään vastaavasti kuin tasossa: kaksi kappaletta ovat yhdenmuotoisia, jos niiden vastinjanat ovat verrannolliset. Kolme kuutiota on muodostettu yhdenmuotoisista kappaleista. Särmien pituuksien suhde on 1 : 2 : 3 ja tilavuuksien suhde 1 : 8 : 27.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Pituuksien ja tilavuuksien suhteiden välillä on myös selvä yhteys. Tilavuuksien suhteet voidaan kirjoittaa pituuksien suhteiden avulla seuraavasti: 13 : 23 : 33.
Yhdenmuotoisten kappaleiden tilavuuksien suhde on verrannollinen pituuksien suhteiden kuutioon.
Säännölliset monitahokkaat ovat keskenään yhdenmuotoisia: kaikki tetraedrit ovat keskenään yhdenmuotoisia, kaikki kuutiot ovat keskenään yhdenmuotoisia jne.
Esimerkki 1.
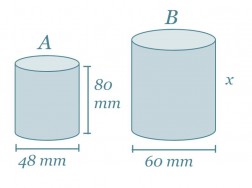
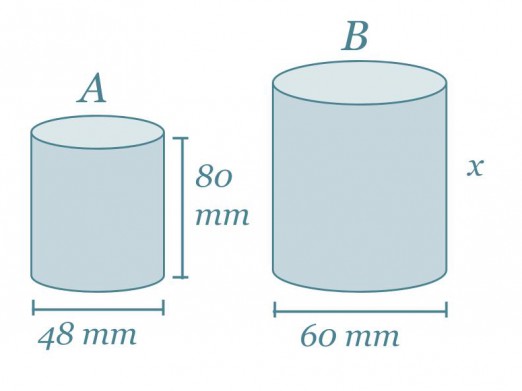
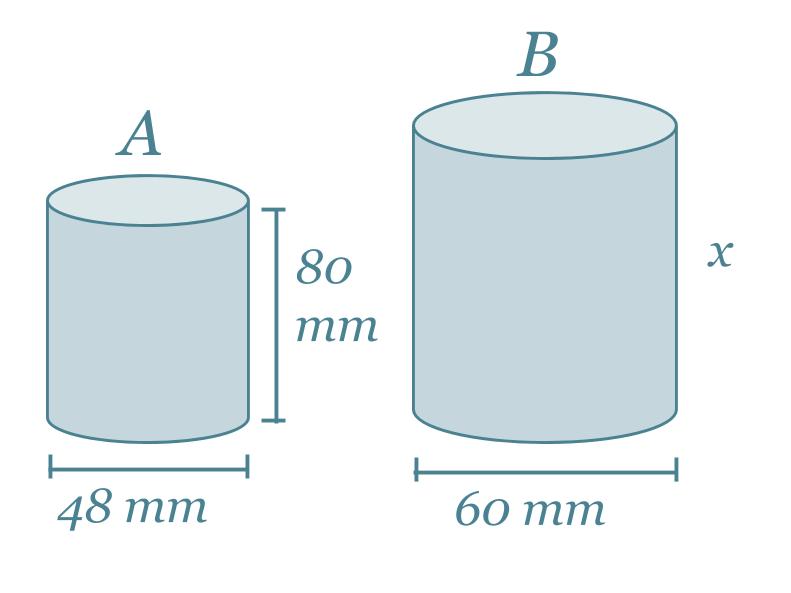
Lieriöt A ja B ovat yhdenmuotoisia. Lieriön A pinta-ala on 15700 mm2 ja tilavuus 145000 mm3. Laske lieriön A tietoja hyväksi käyttäen lieriön B
a) korkeus
b) pinta-ala
c) tilavuus.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
a) Yhdenmuotoisten kappaleiden pituuksien suhde on vakio.
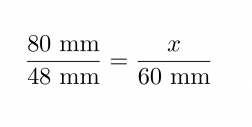
Klikkaa kuva suuremmaksi!
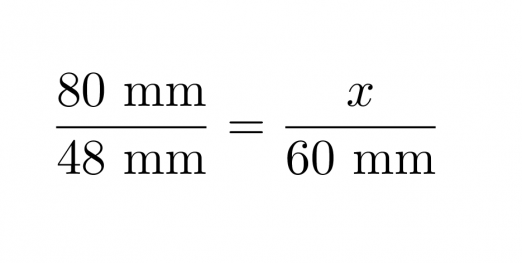
Klikkaa kuva suuremmaksi!
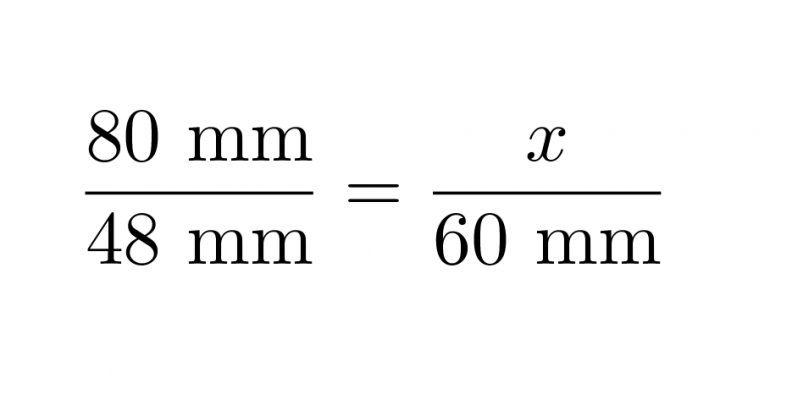
Klikkaa kuva suuremmaksi!
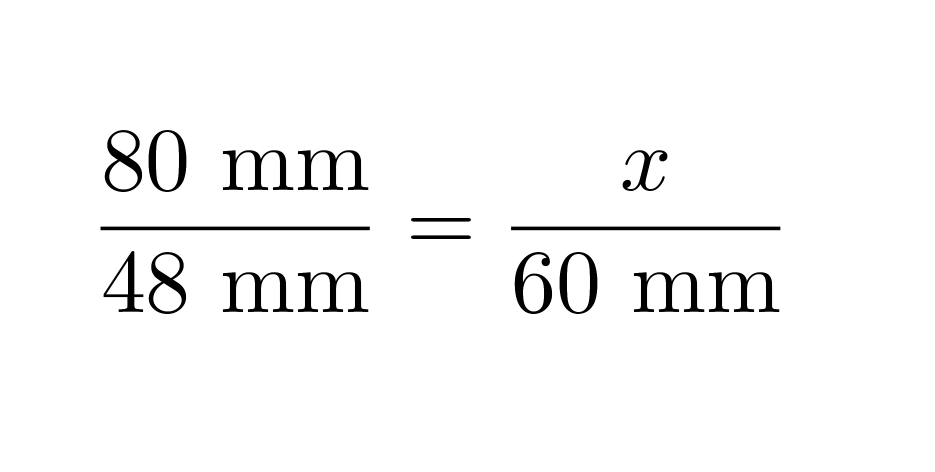
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
josta ristiin kertomalla ja sieventämällä saadaan x = 100 mm.
b) Yhdenmuotoisten kappaleiden pinta-alojen suhde on yhtä suuri kuin pituuksien suhteiden neliö.
Valitaan tarkastelupituuksiksi lieriöiden halkaisijat.
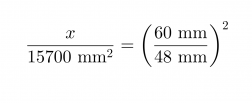
Klikkaa kuva suuremmaksi!
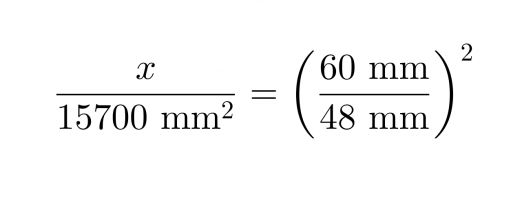
Klikkaa kuva suuremmaksi!
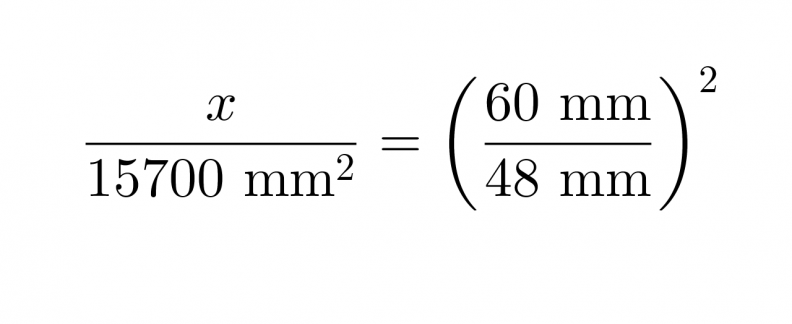
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
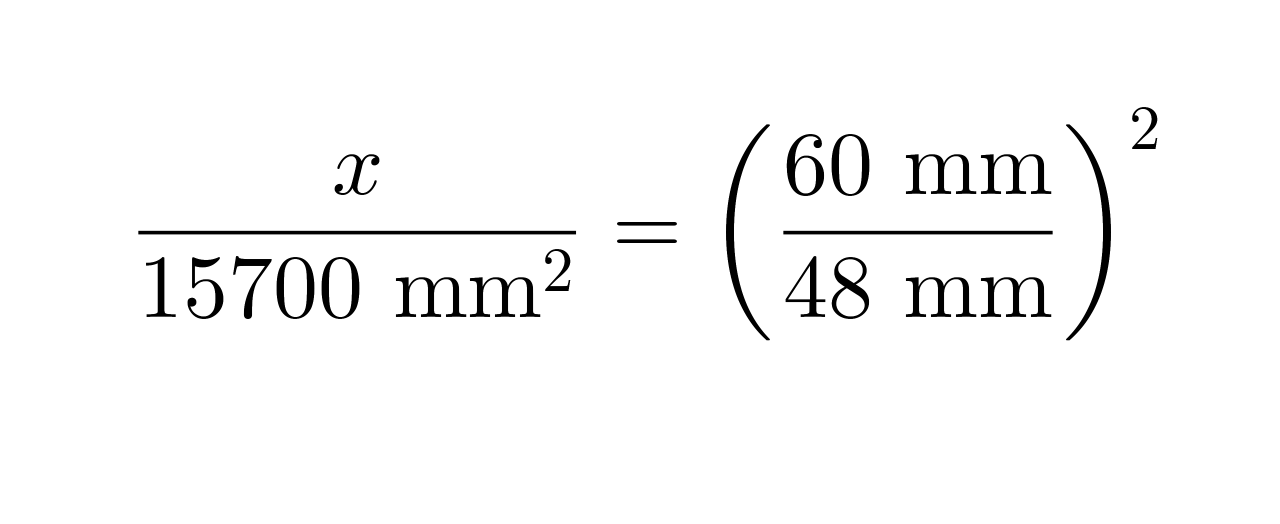
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yleisiä potenssisääntöjä soveltaen saadaan yhtälö muotoon
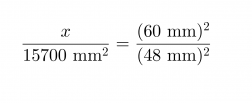
Klikkaa kuva suuremmaksi!
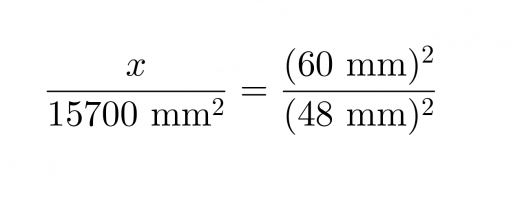
Klikkaa kuva suuremmaksi!
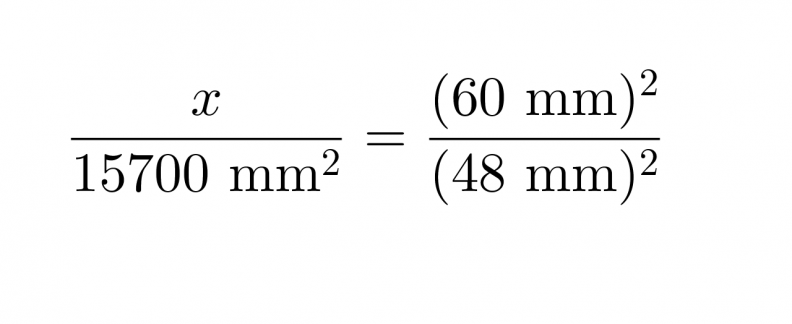
Klikkaa kuva suuremmaksi!
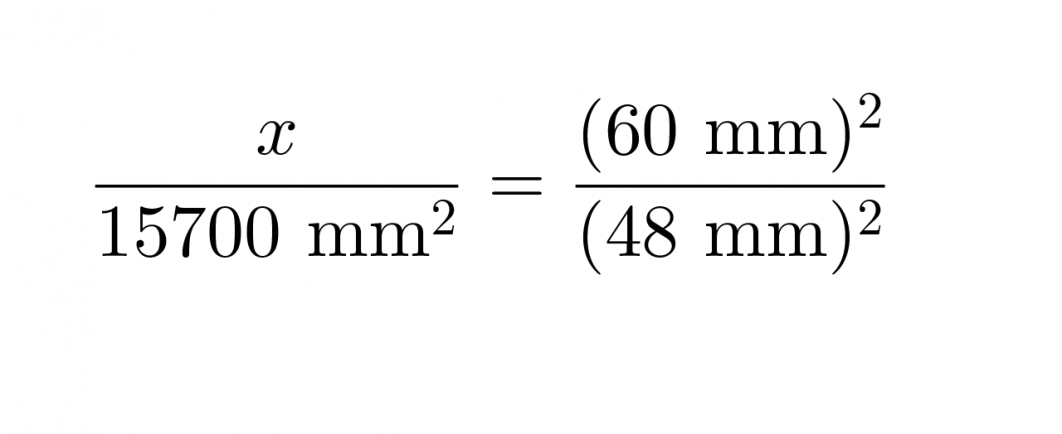
Klikkaa kuva suuremmaksi!
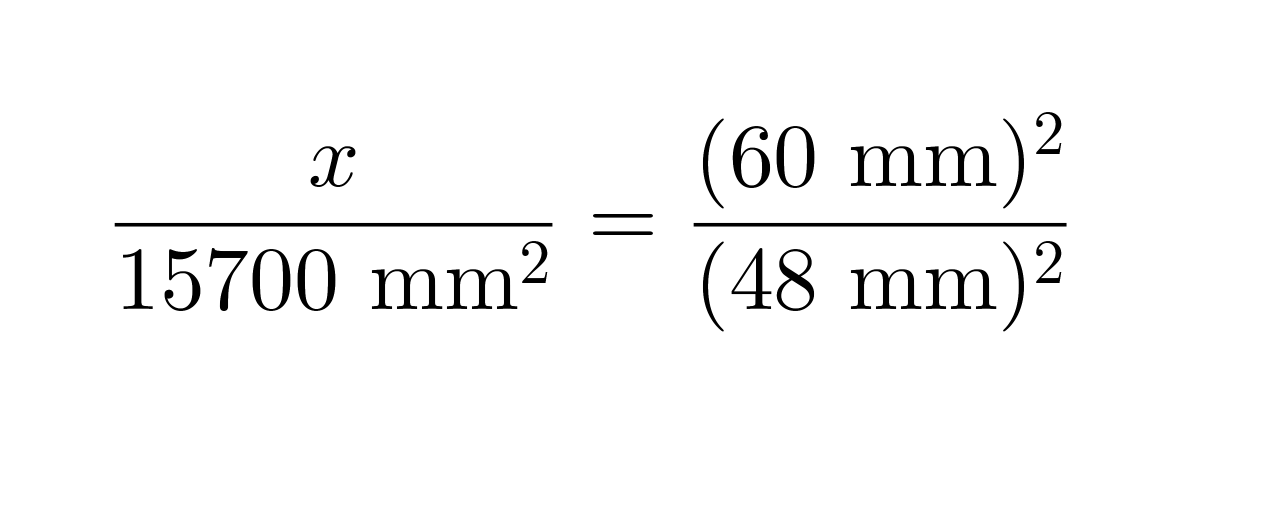
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ristiin kertomalla ja yhtälön ratkaisusääntöjä soveltamalla saadaan x = 24500 mm2.
c) Yhdenmuotoisten kappaleiden tilavuuksien suhde on yhtä suuri kuin pituuksien suhteiden kuutio.
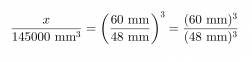
Klikkaa kuva suuremmaksi!
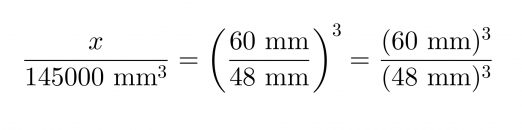
Klikkaa kuva suuremmaksi!
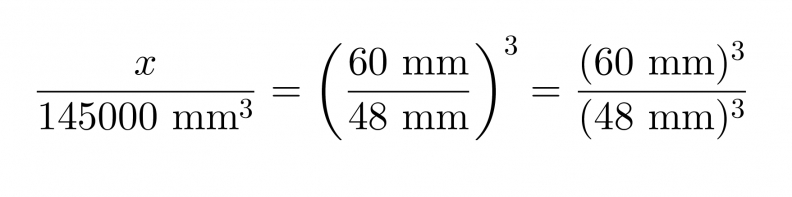
Klikkaa kuva suuremmaksi!
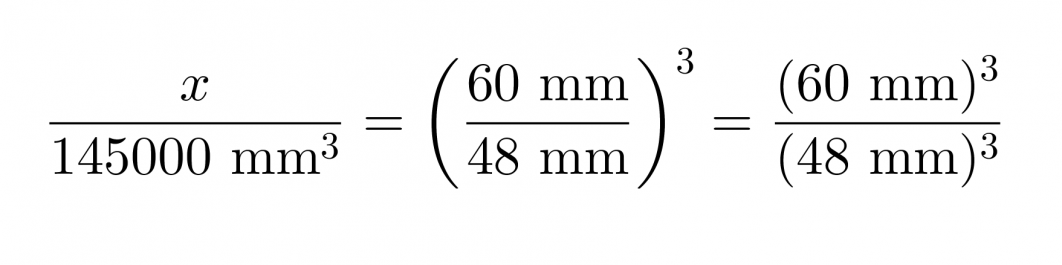
Klikkaa kuva suuremmaksi!
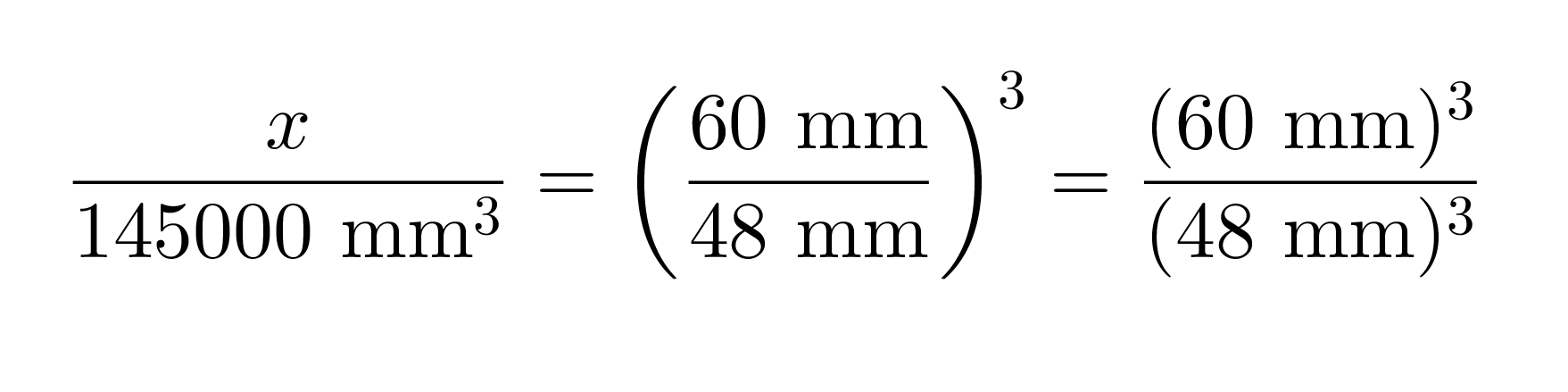
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisuksi saadaan x = 283000 mm3.
Vastaus: Lieriön B korkeus on 100 mm, pinta-ala 245 cm2 ja tilavuus 283 cm3.
Esimerkki 2.
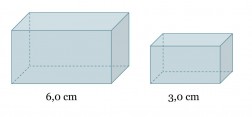
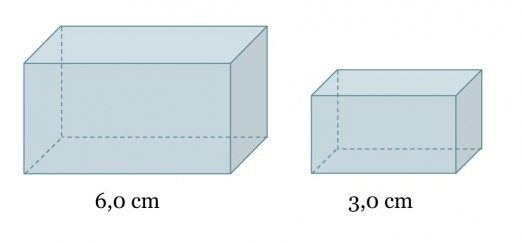
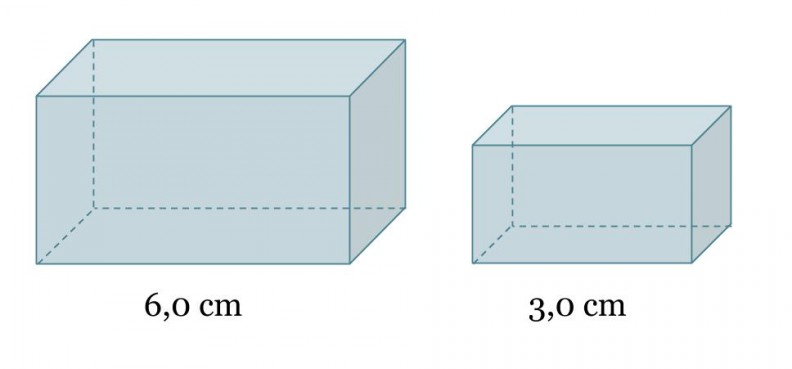
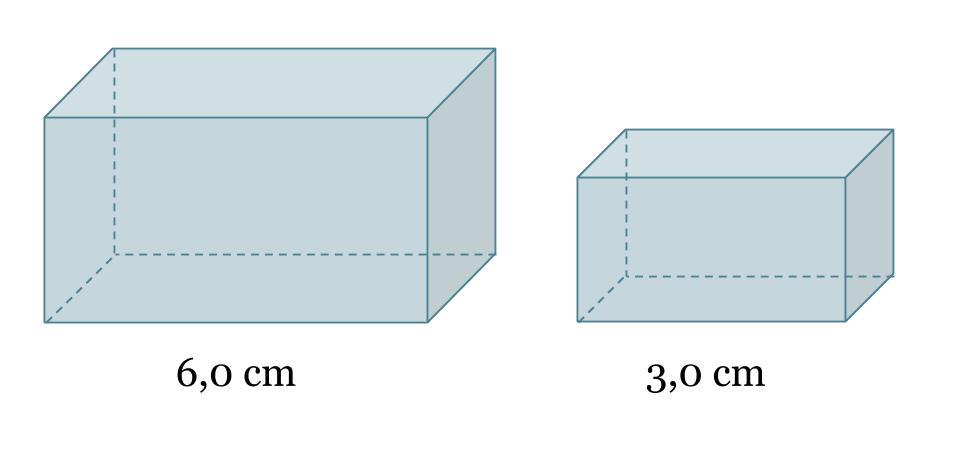
Kuvan suorakulmaiset särmiöt ovat yhdenmuotoisia ja suuremman särmiön tilavuus on 36 cm3. Mikä on pienemmän särmiön tilavuus?
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
Yhdenmuotoisten kappaleiden tilavuuksien suhde on yhtä suuri kuin pituuksien suhteiden kuutio. Olkoon pienemmän särmiön tilavuus x.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Pienemmän särmiön tilavuus on 4,5 cm3.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014