16. Tiheys*
Kansankielessä painolla tarkoitetaan yleensä massaa. Massa ja paino ovat kuitenkin eri suureita. Massan yksikkö on kilogramma ja painon newton. Yhden kilogramman punnusta Maa vetää puoleensa 9,8 newtonin voimalla. Joudumme siis tekemään töitä 9,8 newtonin voimalla pitäessämme punnusta kädessämme. Vaa’at mittaavat kappaleen painoa eikä massaa, vaikka niissä käytetäänkin massan yksiköitä, kilogrammoja. Koska vetovoima on suunnilleen sama kaikkialla Maapallon pinnalla, voidaan vaan asteikko kalibroida näyttämään suoraan kilogrammoja.
Kappaleen painolla on merkitystä vain, kun kappale sijaitsee jossakin vetovoimakentässä. Painosi Kuussa on kuudesosa painostasi Maassa, koska Kuu pystyy vetämään sinua puoleensa vain kuudesosalla siitä voimasta, joka pitää sinut maapallon pinnalla. Olit sitten Kuussa tai Maassa massasi pysyy kuitenkin samana. Koostut molemmissa paikoissa ihan samoista aineista.
Kappaleen massa ei riipu pelkästään kappaleen koosta, vaan myös siitä, mistä aineesta kappale on tehty eli aineen tiheydestä, jota merkitään kreikkalaisella kirjaimella ρ (lausutaan: roo).
Kun tiedetään kappaleen massa m ja tilavuus V, voidaan sen tiheys laskea kaavalla
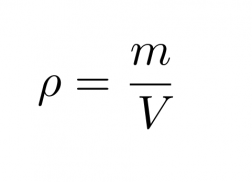
Klikkaa kuva suuremmaksi!
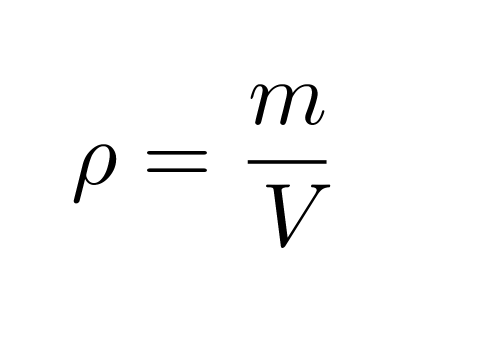
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
SI-järjestelmän mukainen tiheyden yksikkö on kg/m3. Veden tiheys on 1000 kg/m3 ja ilman tiheys merenpinnan tasolla on 1,29 kg/m3.
Asukastiheys
Väestön lukumäärän eli väkiluvun suhteen asuma-alueeseen osoittaa väestöntiheys eli asukastiheys, jonka yksikkö on tavallisesti as/km2.
Asukastiheys kuvaa kuinka miehitetty alue on ja se lasketaan kaavalla
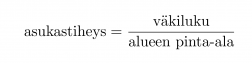
Klikkaa kuva suuremmaksi!
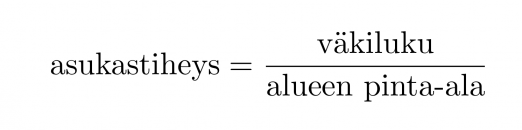
Klikkaa kuva suuremmaksi!
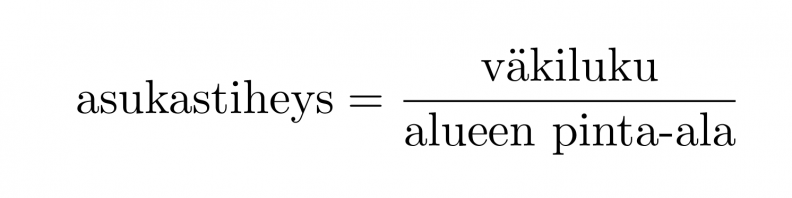
Klikkaa kuva suuremmaksi!
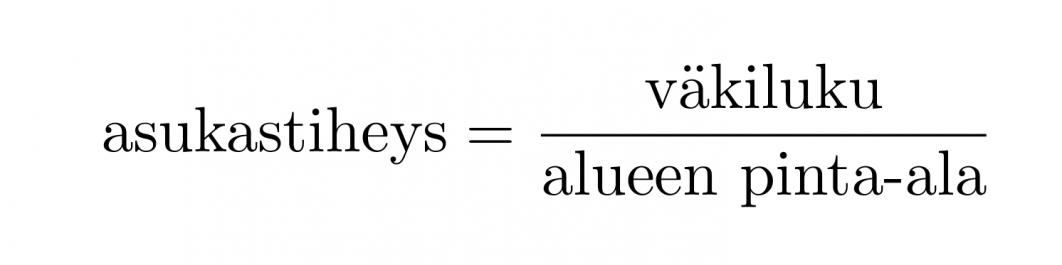
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
Mitä ainetta on pallo, jonka massa on 21,7 kg ja säde 87 mm?
Ratkaisu:
Jos laskemme pallon tiheyden, saamme tiheystaulukon avulla selville aineen, josta pallo on valmistettu. Tiheystaulukossa on tiheydet annettu yksiköissä kg/dm3. Jotta vältytään myöhemmältä yksiköiden muuntamiselta, kannattaa pallon säde sijoittaa laskukaavaan desimetreissä.
Lasketaan ensiksi pallon tilavuus.
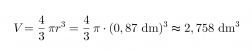
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
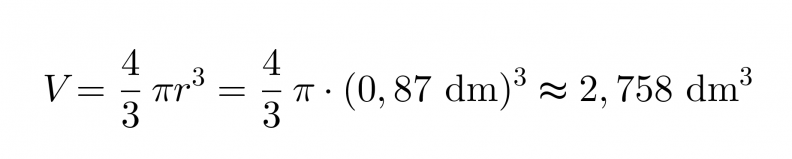
Klikkaa kuva suuremmaksi!
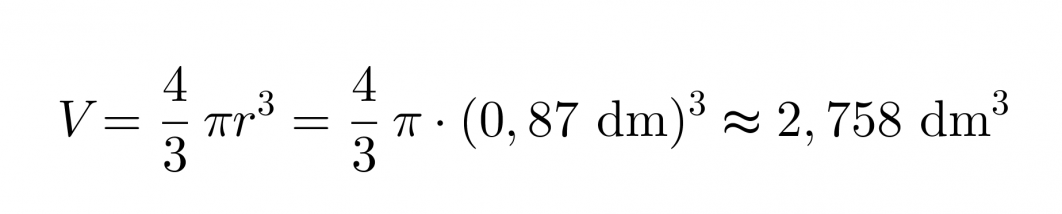
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tiheydeksi tällöin saadaan
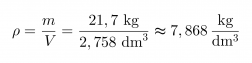
Klikkaa kuva suuremmaksi!
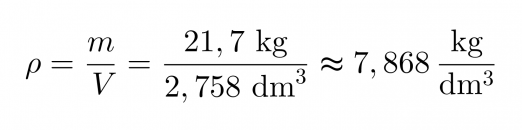
Klikkaa kuva suuremmaksi!
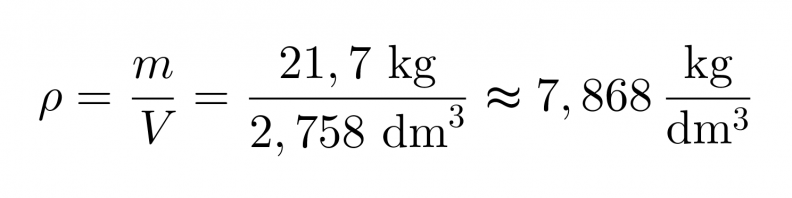
Klikkaa kuva suuremmaksi!
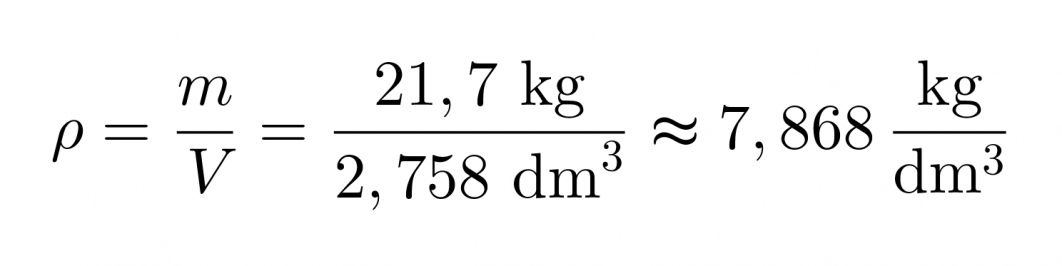
Klikkaa kuva suuremmaksi!
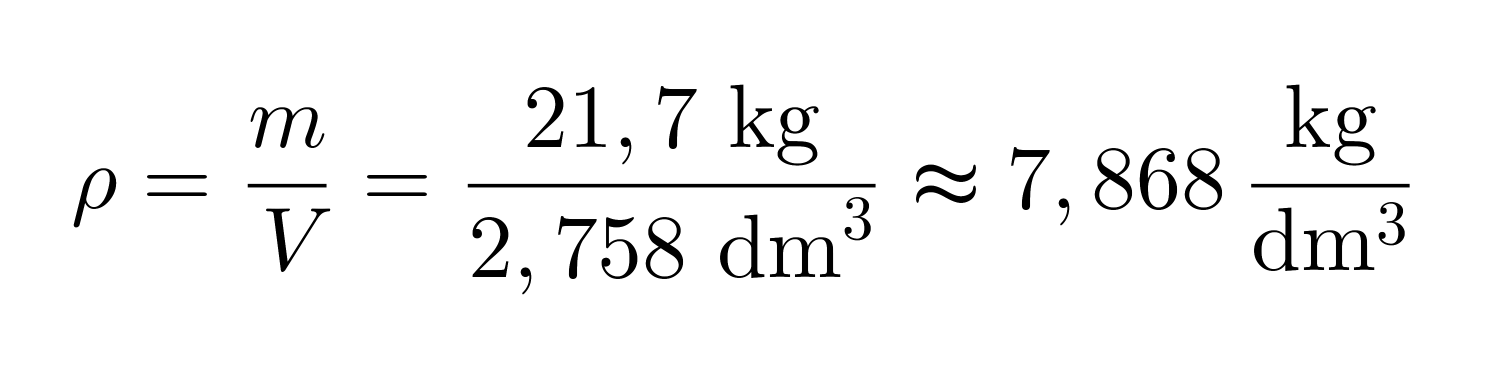
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Raudan tiheys on kirjan taulukko-osion Alkuaineiden ominaisuuksia -taulukon mukaan 7,87 kg/dm3, joka on hyvin lähellä saamaamme tiheyttä.
Vastaus: Pallo on rautaa.
Esimerkki 2.
Omakotitalon katolle, jonka pinta-ala on 150 m2, kertyy 15 cm paksu lumikerros. Likimäärin 1 cm lunta on sulatettuna 1 mm vettä. Paljonko on katolla olevan lumen massa?
Ratkaisu:
Lumen voidaan ajatella muodostavan katolle suorakulmaisen särmiön, jonka tilavuudeksi saadaan V = 150 m2 · 0,015 m = 2,25 m3.
Veden tiheys on 1000 kg/m3. Tiheyden kaavasta saadaan massa ratkaistua kaavalla:
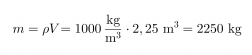
Klikkaa kuva suuremmaksi!
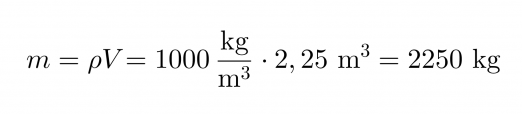
Klikkaa kuva suuremmaksi!
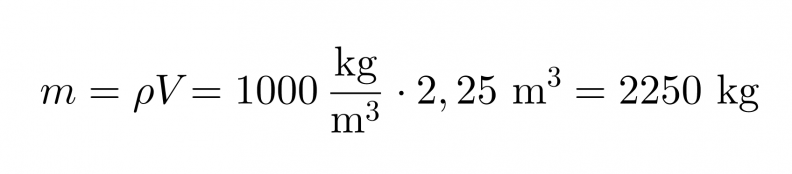
Klikkaa kuva suuremmaksi!
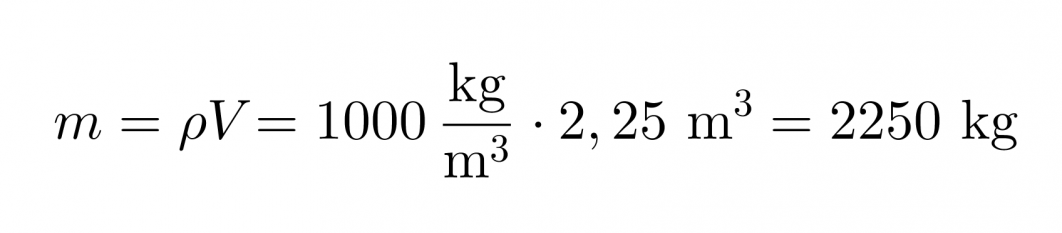
Klikkaa kuva suuremmaksi!
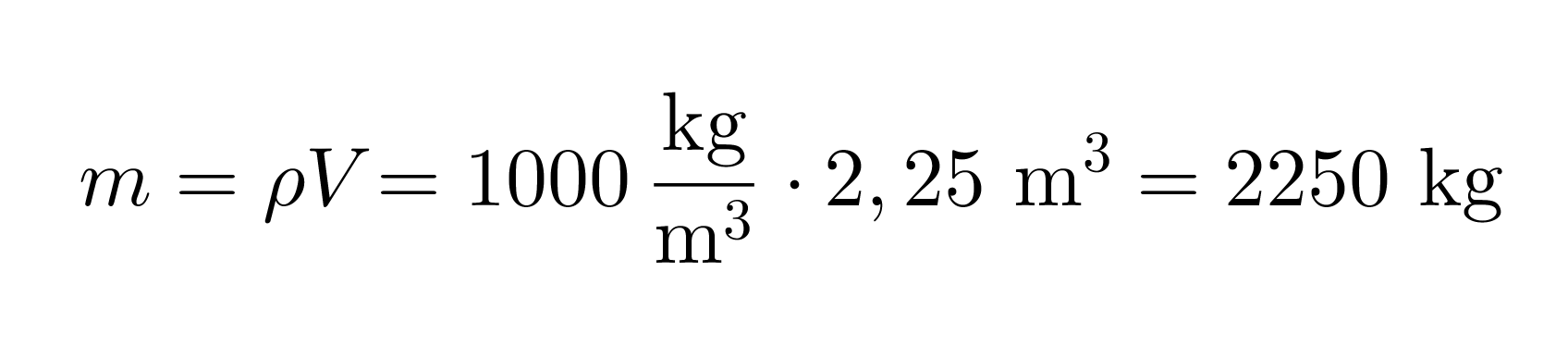
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Lumen massa on 2300 kg.
Esimerkki 3.
Paljonko Ranskassa on asukkaita, kun sen asukastiheys on 107,2 as/km2 ja pinta-ala 543 965 km2 ?
Ratkaisu:
Asukastiheyden yhtälöstä saadaan väkiluvun ratkaisukaavaksi:

Klikkaa kuva suuremmaksi!
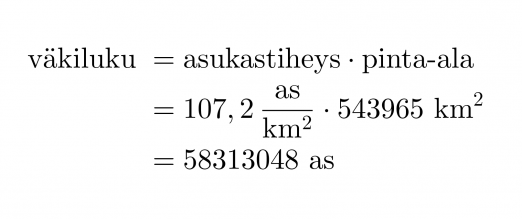
Klikkaa kuva suuremmaksi!
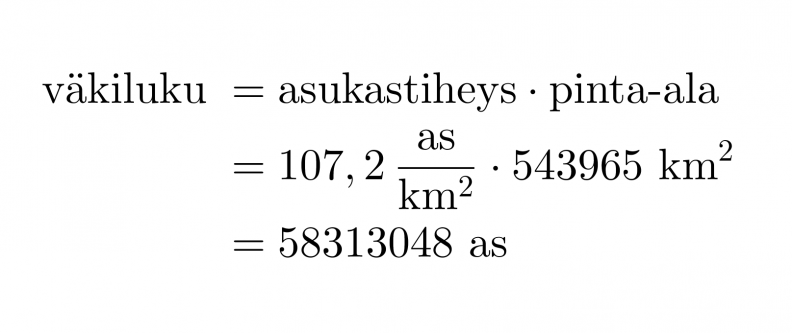
Klikkaa kuva suuremmaksi!
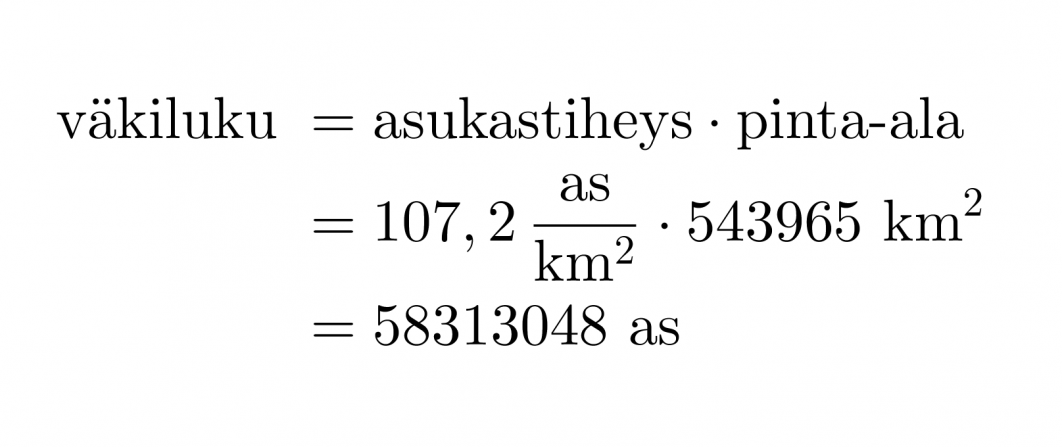
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: 58,31 miljoonaa asukasta
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014