17. Symmetria

Jo­kai­sel­la kap­pa­leel­la on ole­mas­sa pai­no­pis­te. Jos kap­pa­let­ta tu­e­taan sen pai­no­pis­tees­tä, py­syy se tasa­pai­nos­sa mis­sä asen­nos­sa hy­vän­sä. Kap­pa­leen koko mas­san voi­daan aja­tel­la si­jait­se­van sen pai­no­pis­tees­sä ja sik­si sitä usein kut­su­taan­kin mas­sa­kes­ki­pis­teek­si.

Klik­kaa kuva suu­rem­mak­si!

Sym­met­ri­sen kap­pa­leen mas­sa­kes­ki­pis­te si­jait­see sen sym­met­ri­a­kes­kuk­ses­sa, sym­met­ria-ak­se­lil­la tai sym­met­ri­a­ta­sos­sa, kun ge­o­met­ri­sen muo­don li­säk­si myös mas­sa on ja­kau­tu­nut ta­sai­ses­ti. Sym­met­ria-ak­se­li on se suo­ra, jon­ka suh­teen ku­vio tai kap­pa­le ku­vau­tuu it­sel­leen eli täs­mäl­leen sa­maan paik­kaan, jos­sa se alun­pe­rin­kin oli. Pis­teen suh­teen sym­met­ri­nen ku­vio tai kap­pa­le ku­vau­tuu it­sel­leen, kun se pei­la­taan kes­ki­pis­tees­sä si­jait­se­van sym­met­ri­a­kes­kuk­sen suh­teen. Kol­mi­u­lot­tei­sil­la kap­pa­leil­la voi myös olla sym­met­ri­a­ta­so­ja, jot­ka ku­vaa­vat nor­maa­lin pei­lin ta­voin kap­pa­leen toi­sen puo­len.

Esimerkki 1.

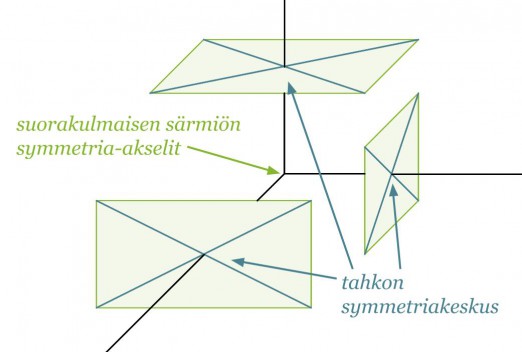
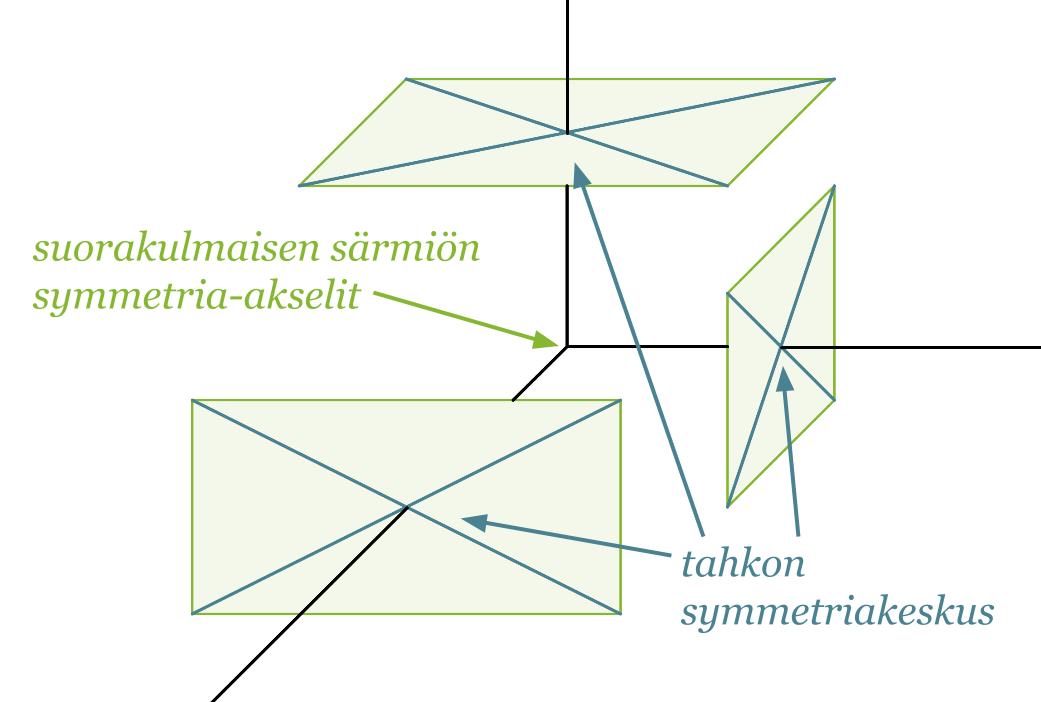
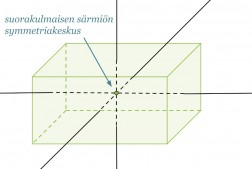
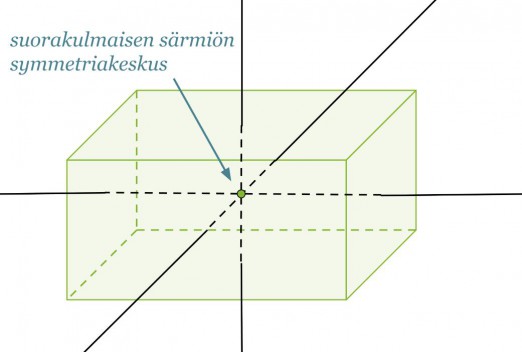
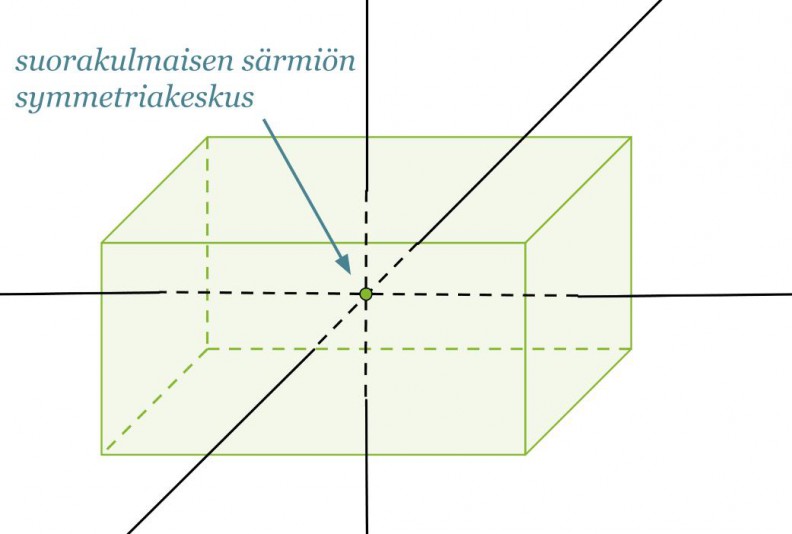
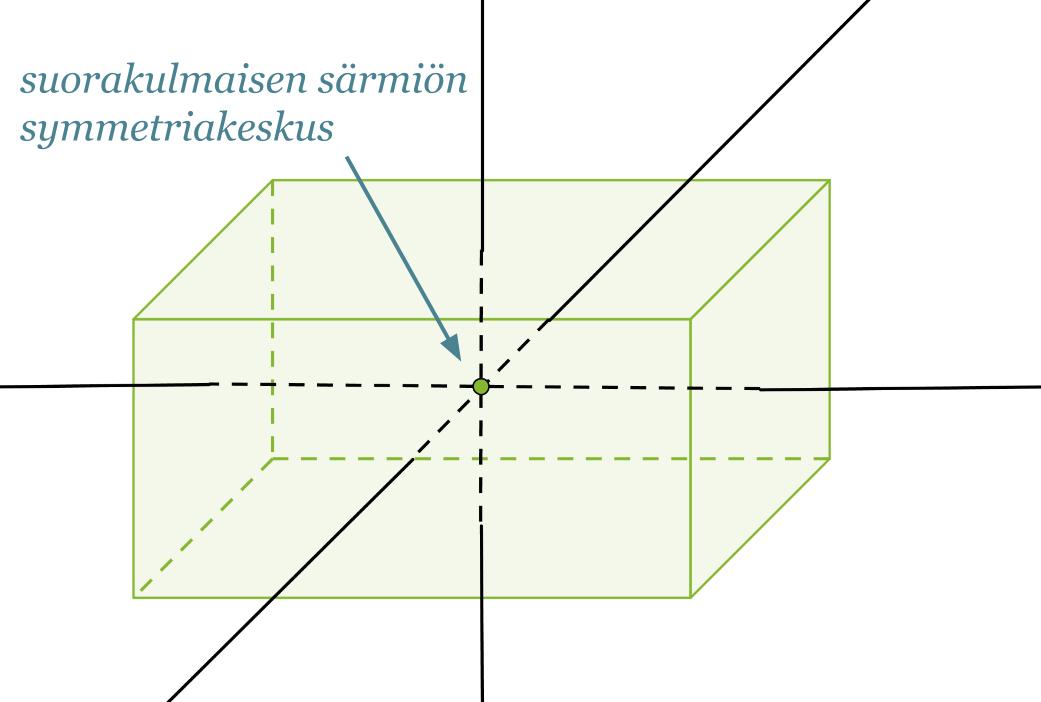
Suo­ra­kul­mai­sel­la sär­mi­öl­lä on kol­me sym­met­ria-ak­se­lia, jot­ka kul­ke­vat vas­tak­kais­ten tah­ko­jen sym­met­ri­a­kes­kuk­sien kaut­ta. Suo­ra­kul­mai­sen sär­mi­ön sym­met­ri­a­kes­kus puo­les­taan si­jait­see sym­met­ria-ak­se­lien leik­kaus­pis­tees­sä.

Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

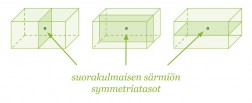
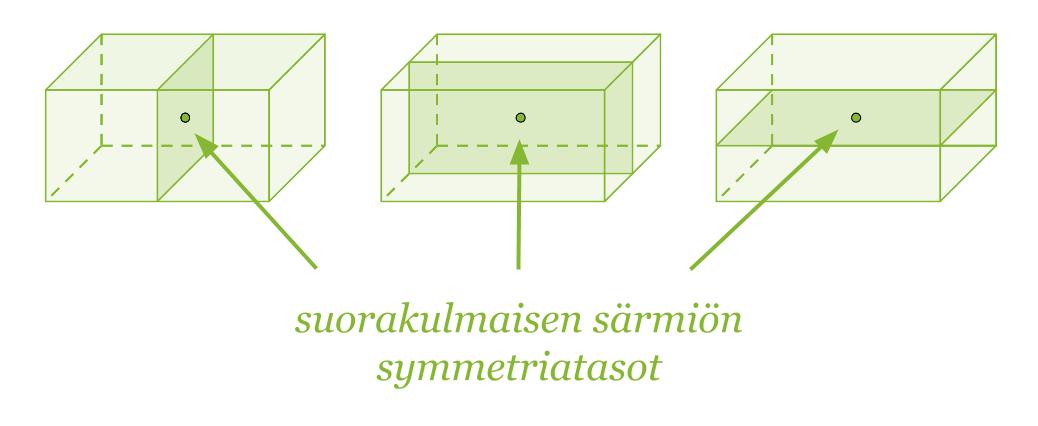
Suo­ra­kul­mai­sen sär­mi­ön sym­met­ri­a­ta­sot ovat kap­pa­leen sym­met­ri­a­kes­kuk­ses­sa ja ne ovat tah­ko­jen kans­sa yh­den­suun­tai­sia.

Klik­kaa kuva suu­rem­mak­si!