18. Geometrian todistuksia*
Onko kolmion kulmien summa todella 180˚? Voisimme piirtää joukon erilaisia kolmiota ja mitata kunkin kolmion kulmat erikseen ja laskea ne yhteen. Kolmion kulmien summaksi tulisi ehkä jotain 178 asteen ja 182 asteen väliltä. Voisimme olettaa väitteen pitävän aika hyvin paikkaansa. Matematiikassa tällainen toiminta ei ole väitteen todistamista vaan pikemminkin likimääräistä arviointia siitä, voisiko väite edes pitää paikkaansa.
Väite pitää todistaa oikeaksi siten, että se pitää paikkansa millä tahansa lukuarvoilla eli todistuksen on oltava yleispätevä. Matematiikassa tärkeät todistetut faktat kirjataan lauseiksi. Lauseiden todistukset perustuvat aiempiin todistuksiin, joiden pohjana on ilman todistamista hyväksytyt perustiedot, joita sanotaan aksioomiksi. Todistustehtävässä on yleensä kolme osaa: oletus, väite ja todistus.
Esimerkki 1.
Todistetaan, että kolmion kulmien summa on 180°.
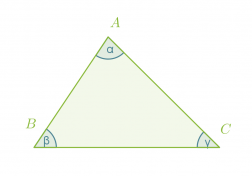
Oletus: Kolmion ABC kulmien suuruudet α, β ja γ.
Väite: Kolmion kulmien summa on 180°.
Todistus:
Piirretään aluksi kolmio ABC ja merkitään sen kulmia muuttujilla α, β ja γ. Koska todistuksen pitää olla yleispätevä, ei voida valita joitain tiettyjä lukuarvoja kulmille.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
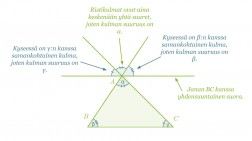
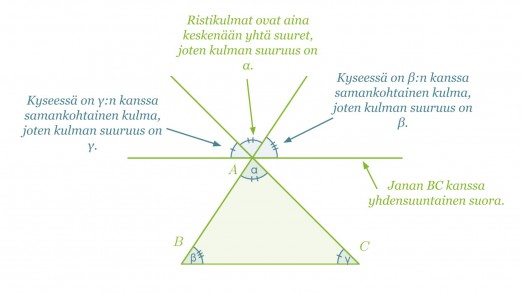
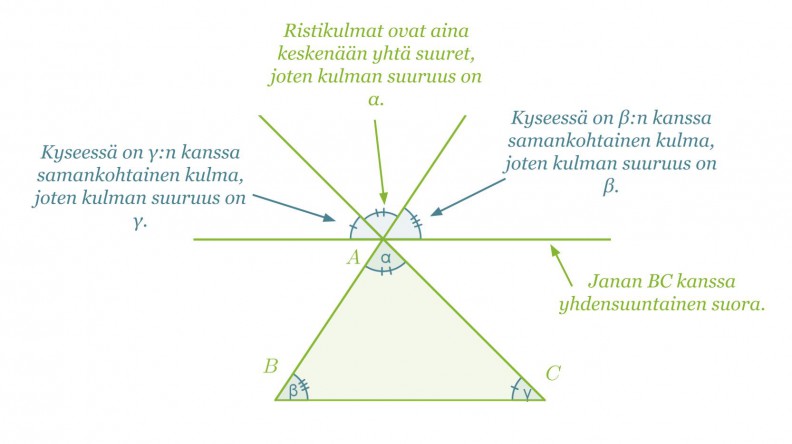
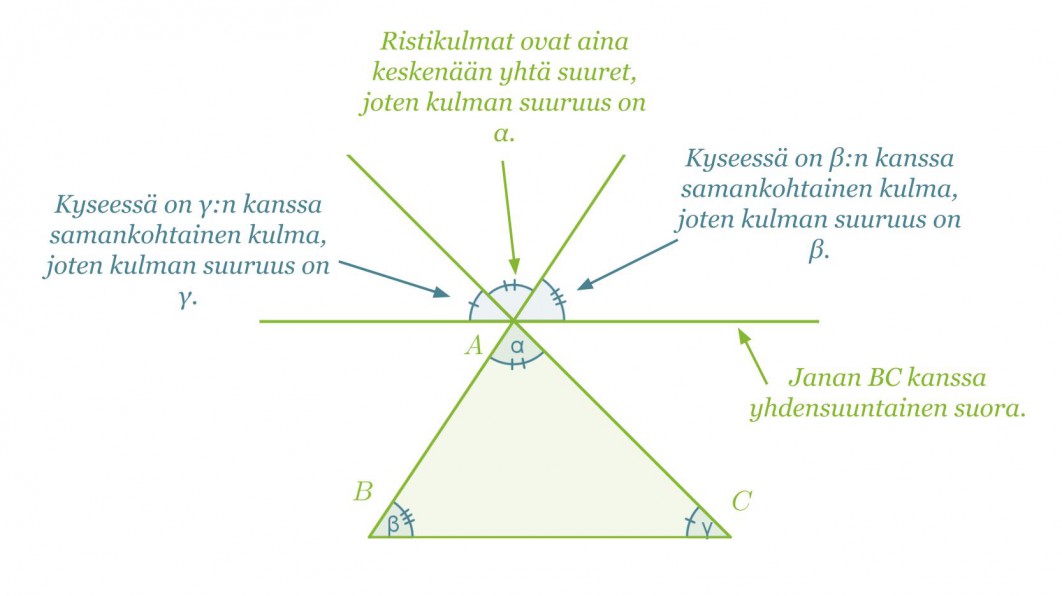
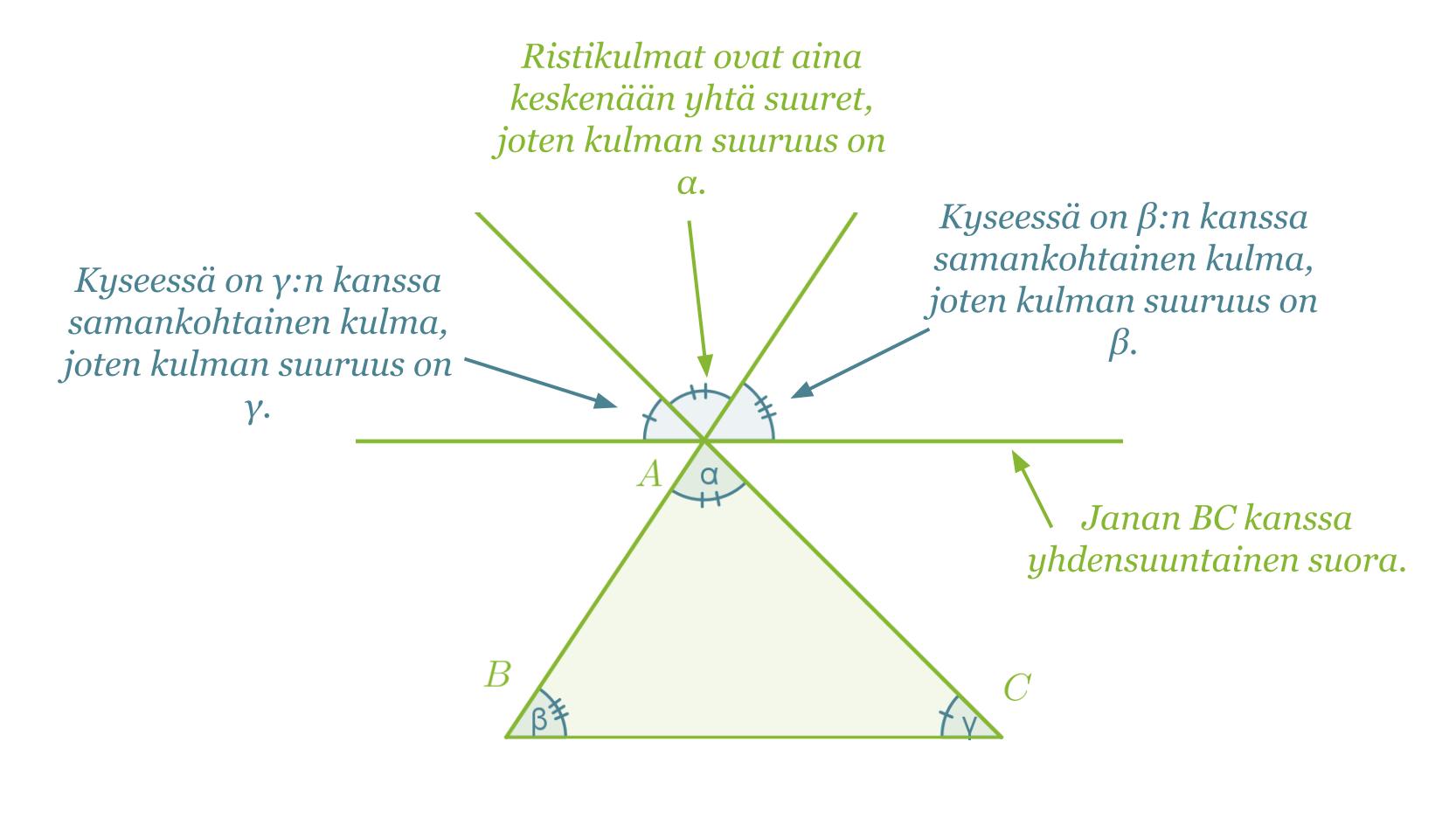
Todistamisen ideana on hyödyntää aikaisempia yleisiä tietoja kulmista. Piirretään kantasivun BC kanssa yhdensuuntainen suora, joka kulkee pisteen A kautta. Piirretään lisäksi sivujen BA ja CA jatkeet.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kulma, joka muodostuu kulmista α, β ja γ, on oikokulma, jolloin väistämättä α + β + γ = 180°. Väite on siis tosi.
Esimerkki 2.
Todistetaan Pythagoraan lause oikeaksi.
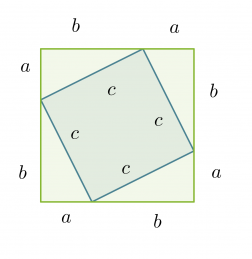
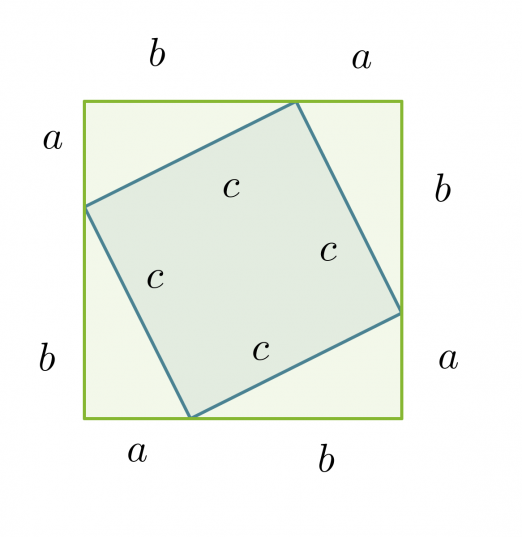
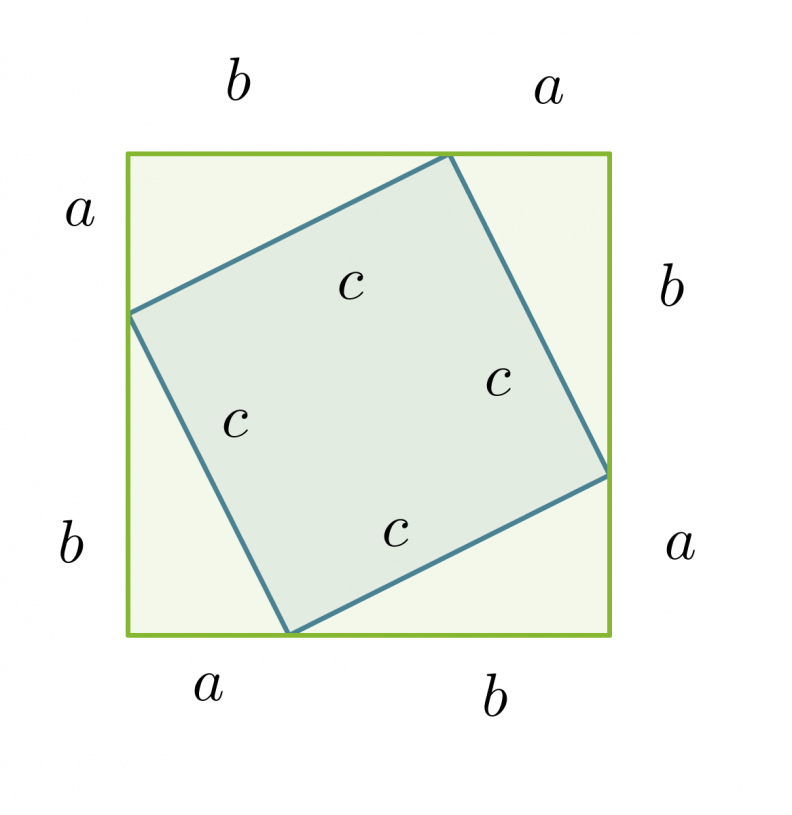
Oletus: Suorakulmaisen kolmion kateettien pituudet ovat a ja b ja hypotenuusan pituus on c.
Väite: a2 + b2 = c2
Todistus
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
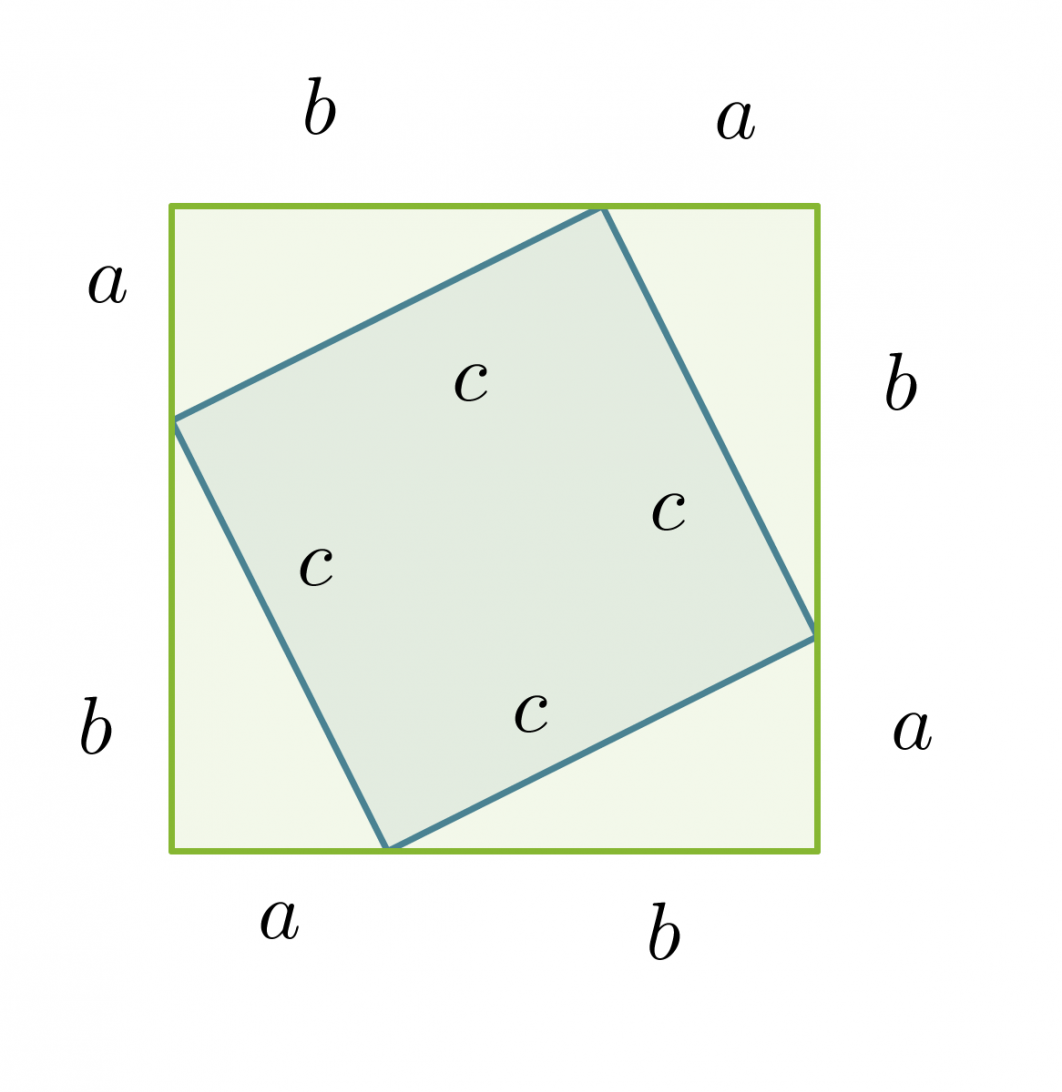
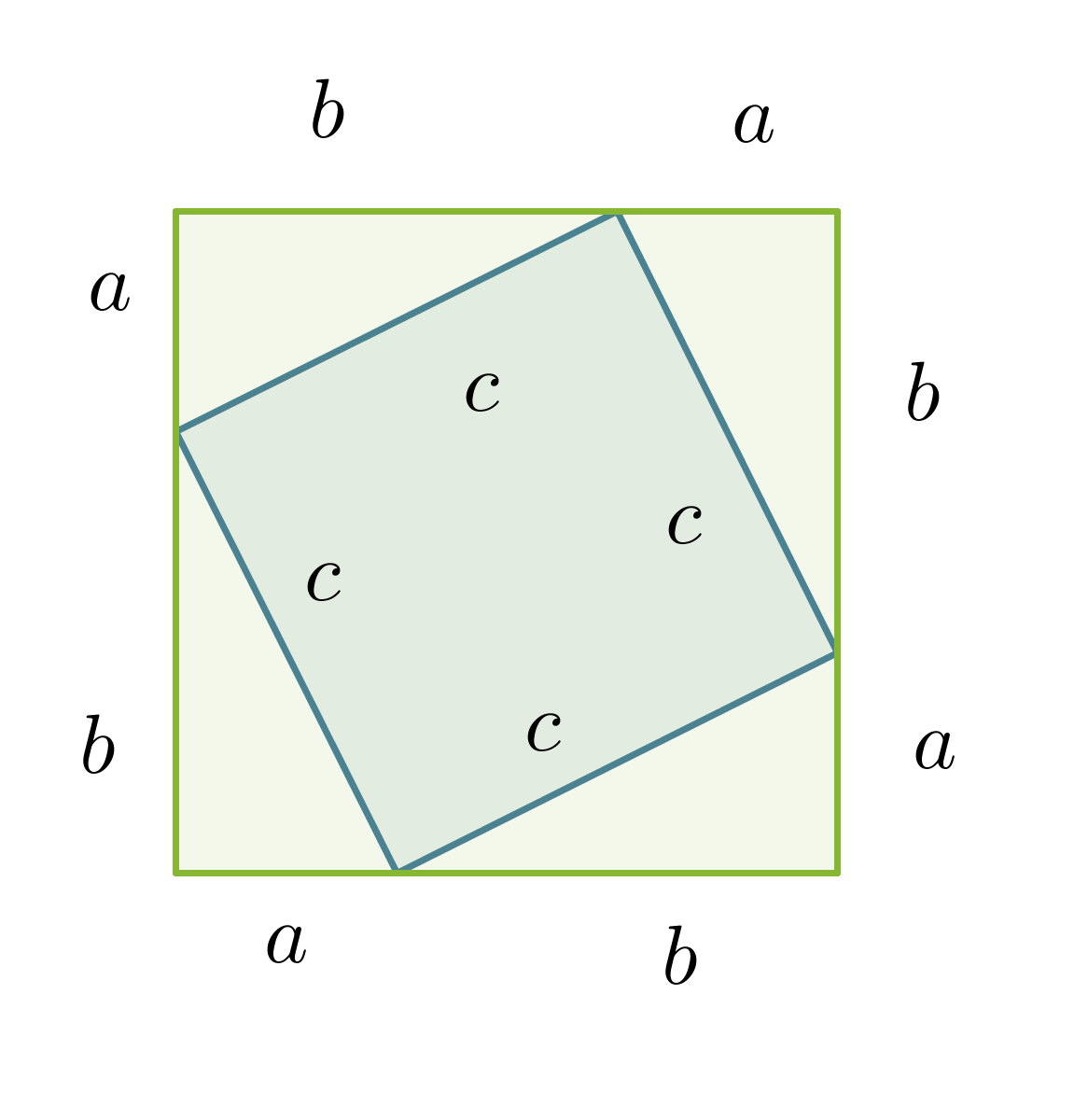
Suuremman neliön pinta-ala on
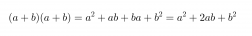
Klikkaa kuva suuremmaksi!
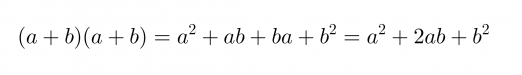
Klikkaa kuva suuremmaksi!
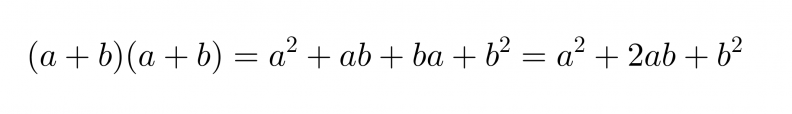
Klikkaa kuva suuremmaksi!
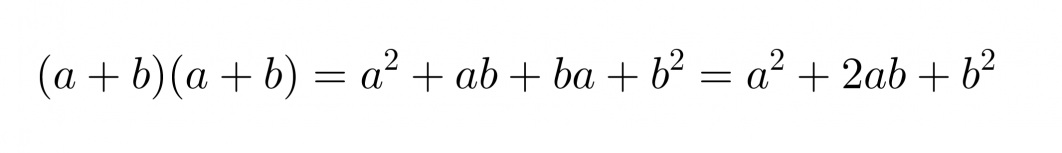
Klikkaa kuva suuremmaksi!
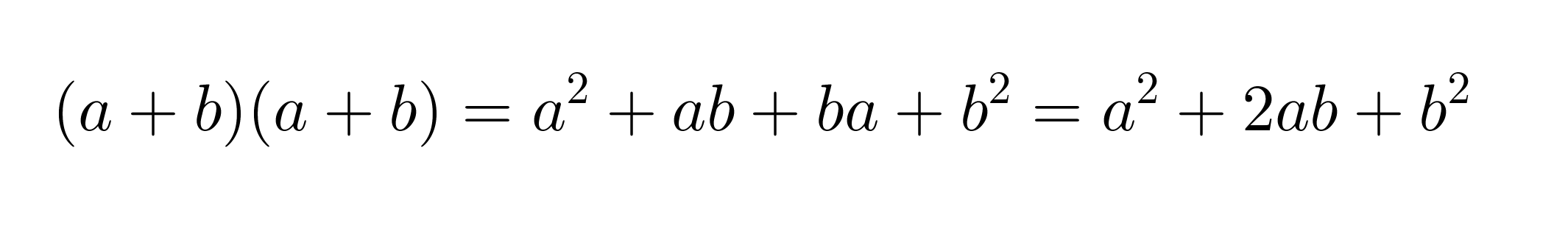
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Toisaalta suuremman neliön pinta-ala saadaan laskemalla yhteen pienemmän neliön pinta-ala ja neljän kolmion pinta-alat.
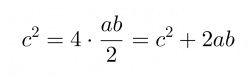
Klikkaa kuva suuremmaksi!
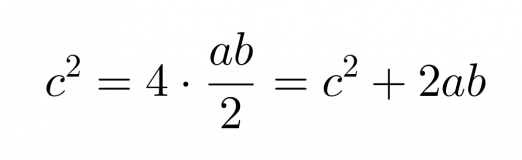
Klikkaa kuva suuremmaksi!
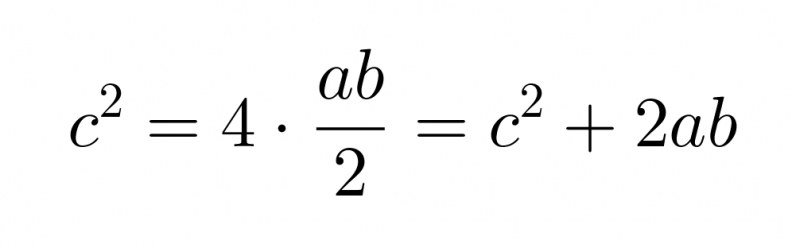
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Edellisten pinta-alojen lausekkeiden on oltava yhtä suuret.
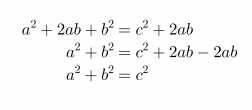
Klikkaa kuva suuremmaksi!
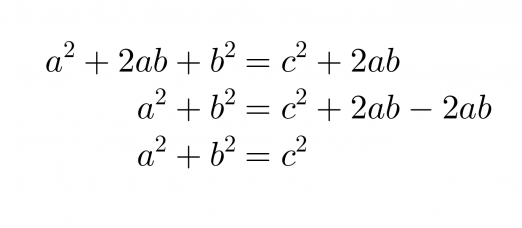
Klikkaa kuva suuremmaksi!
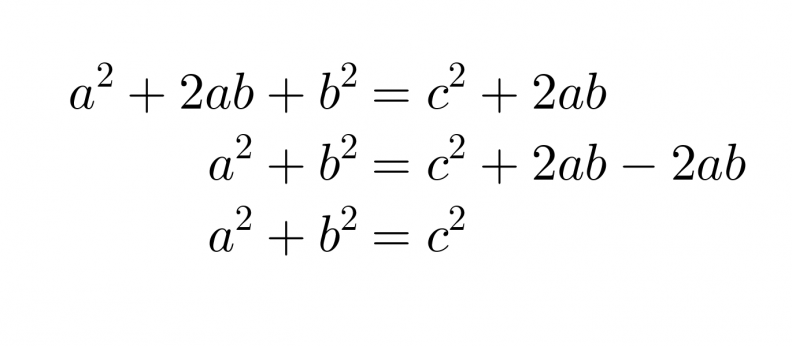
Klikkaa kuva suuremmaksi!
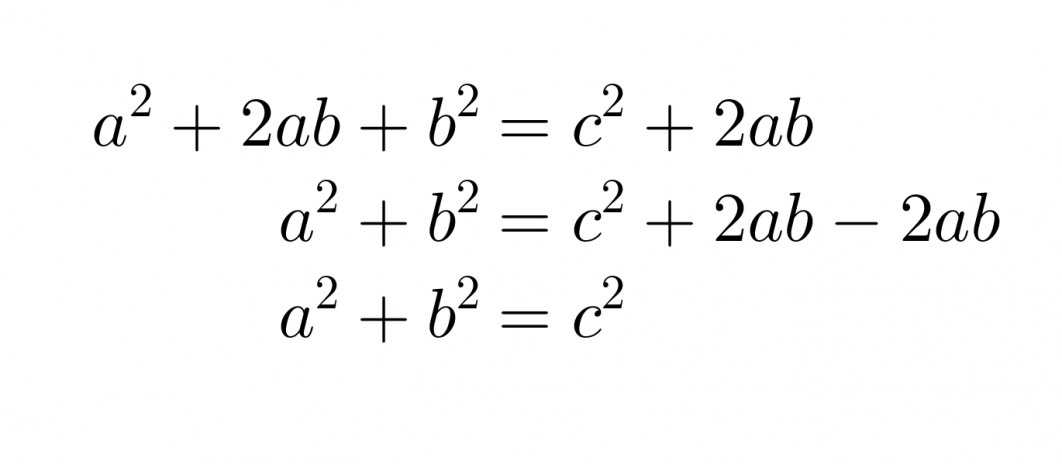
Klikkaa kuva suuremmaksi!
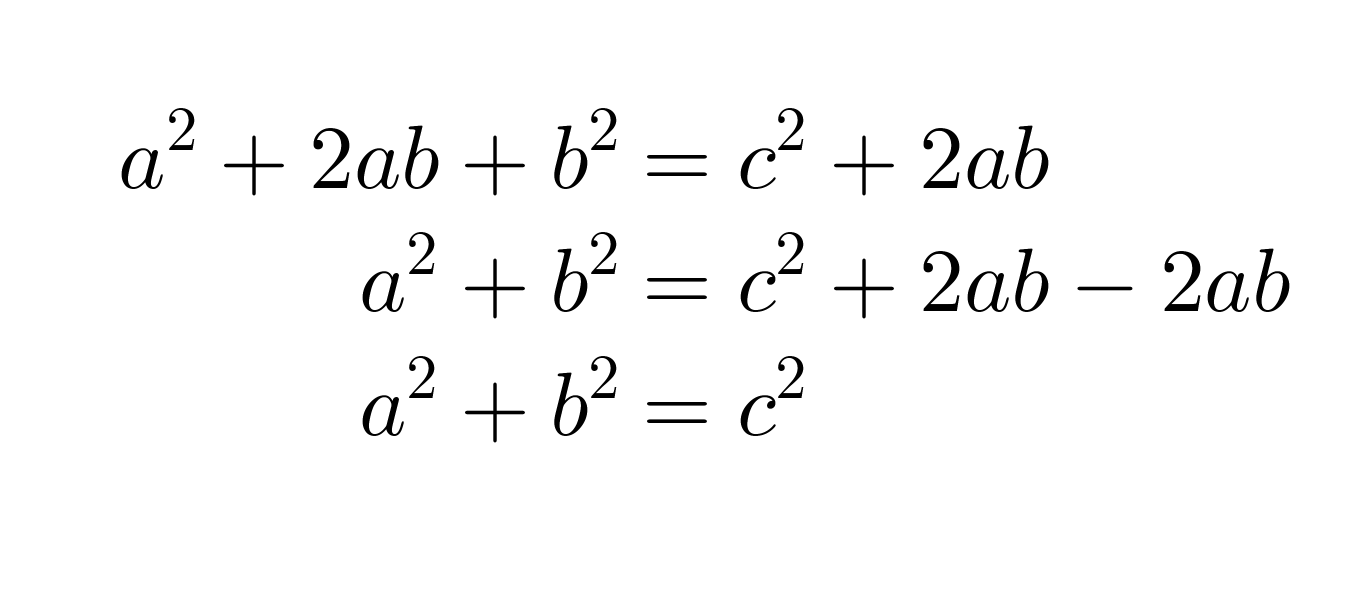
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Väite on siis tosi.
Avoin matematiikka 9Osio 2: Trigonometriaa ja geometrian tietojen syventämistä5.6.2014